Z檢驗
出自 MBA智库百科(https://wiki.mbalib.com/)
Z檢驗(Z Test)
目錄 |
Z檢驗是一般用於大樣本(即樣本容量大於30)平均值差異性檢驗的方法。它是用標準正態分佈的理論來推斷差異發生的概率,從而比較兩個平均數的差異是否顯著。
當已知標準差時,驗證一組數的均值是否與某一期望值相等時,用Z檢驗。
另外,對於Z檢驗我國的統計學教材大多採用U檢驗的說法。而國外英文統計學書籍,大多採用Z檢驗。
Z檢驗的步驟[1]
統計檢驗的基本原理
統計檢驗是先對總體的分佈規律作出某種假說,然後根據樣本提供的數據,通過統計運算,根據運算結果,對假說作出肯定或否定的決策。如果現要檢驗實驗組和對照組的平均數(μ1和μ2)有沒有差異,其步驟為:
1.建立虛無假設,即先認為兩者沒有差異,用 H0:μ1 = μ2 表示;
2.通過統計運算,確定假設 H0 成立的概率 P。
3. 根據 P 的大小,判斷假設 H0 是否成立。如下表所示。
| P值 | H0成立概率大小 | 差異顯著程度 |
|---|---|---|
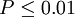 | H0 成立概率極小 | 差異非常顯著 |
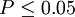 | H0 成立概率較小 | 差異顯著 |
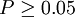 | H0 成立概率較大 | 差異不顯著 |
Z檢驗法適用於大樣本(樣本容量大於30)的兩平均數之間差異顯著性檢驗的方法。它是通過計算兩個平均數之間差的Z分數來與規定的理論Z值相比較,看是否大於規定的理論Z值,從而判定兩平均數的差異是否顯著的一種差異顯著性檢驗方法。其一般步驟:
第一步:建立虛無假設 H0:μ1 = μ2 ,即先假定兩個平均數之間沒有顯著差異,
第二步:計算統計量Z值,對於不同類型的問題選用不同的統計量計算方法,
1、如果檢驗一個樣本平均數( )與一個已知的總體平均數(μ0)的差異是否顯著。其Z值計算公式為:
)與一個已知的總體平均數(μ0)的差異是否顯著。其Z值計算公式為:
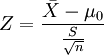
其中:
2、如果檢驗來自兩個的兩組樣本平均數的差異性,從而判斷它們各自代表的總體的差異是否顯著。其Z值計算公式為:
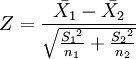
其中:
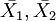 是樣本1,樣本2的平均數;
是樣本1,樣本2的平均數;
- S1,S2是樣本1,樣本2的標準差;
- n1,n2是樣本1,樣本2的容量。
第三步:比較計算所得Z值與理論Z值,推斷發生的概率,依據Z值與差異顯著性關係表作出判斷。如下表所示:
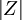 | P值 | 差異程度 |
|---|---|---|
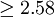 | 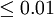 | 非常顯著 |
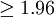 | 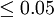 | 顯著 |
| <1.96 | >0.05 | 不顯著 |
第四步:根據是以上分析,結合具體情況,作出結論。
Z檢驗舉例[1]
某項教育技術實驗,對實驗組和控制組的前測和後測的數據分別如下表所示,比較兩組前測和後測是否存在差異。
| 實驗組和控制組的前測和後測數據表 | ||||
|---|---|---|---|---|
| 前測 | 實驗組 | n1 = 50 | 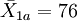 | S1a = 14 |
| 控制組 | n2 = 50 |  | S2a = 16 | |
| 後測 | 實驗組 | n1 = 50 | 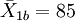 | S1b = 8 |
| 控制組 | n2 = 50 | 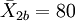 | S2b = 14 | |
由於n>30,屬於大樣本,所以採用Z檢驗。由於這是檢驗來自兩個不同總體的兩個樣本平均數,看它們各自代表的總體的差異是否顯著,所以採用雙總體的Z檢驗方法。
計算前測Z的值:
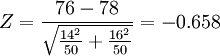
- ∵|Z|=0.658<1.96
- ∴ 前測兩組差異不顯著。
再計算後測Z的值:
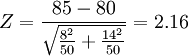
- ∵|Z|= 2.16>1.96
- ∴ 後測兩組差異顯著。
評論(共25條)
兩樣本均值差異比較那裡的公式錯了吧,S的位置應該是S平方.看下麵例子裏就是平方的.
附上參考文獻,希望對你有幫助~
1.96是個什麼值
當概率水平設在0.05的標準時,雙側檢驗的臨界Z值為1.96,臨界值可以通過查正態分佈表獲得。
謝謝,有個問題,最後的舉例的計算中樣本容量n1,n2都是50?n2是否應該改成48?
是啊!
兩樣本均值差異比較那裡的公式錯了吧,S的位置應該是S平方.看下麵例子裏就是平方的.
確實啊
介紹的很好,簡潔易懂。但是我看的z值表中p=0.05時,z值為1.64,p=0.01時,z值為2.32左右。與你上面的判斷值2.58和1.96的差別在什麼地方。能否解釋一下,謝謝
z檢驗,S是不應該是總體的標準差;t檢驗,s才是樣本的標準差嗎
Yes. You're right. In Z-test, we use the variance of population; in T-test, we use the variance of sample.
P值不是 "H0 成立的概率" 而是 "假如H0為真 得到該檢定樣本的概率" 例如 在檢查有沒有生病 抽血得到樣本(病毒的數量) H0:有生病 H1:沒生病 那麼這裡的p值 不是 "生病的機率" 而是 "假如有生病 得到該樣本中病毒數量的機率"








看後思路非常清晰,很有用