平均數
出自 MBA智库百科(https://wiki.mbalib.com/)
平均數(Average)
目錄 |
平均數是統計學中最常用的統計量,用來表明資料中各觀測值相對集中較多的中心位置。在畜牧業、水產業生產實踐和科學研究中,平均數被廣泛用來描述或比較各種技術措施的效果、畜禽某些數量性狀的指標等等。
統計平均數是用於反映現象總體的一般水平,或分佈的集中趨勢。數值平均數是總體標誌總量對比總體單位數而計算的。[1]
- 1、樣本各觀測值與平均數之差的和為零,即離均差之和等於零。
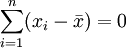 或簡寫成
或簡寫成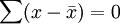
- 2、樣本各觀測值與平均數之差的平方和為最小,即離均差平方和為最小。
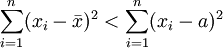 (常數a≠
(常數a≠ )
)
或簡寫為: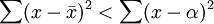
以上兩個性質可用代數方法予以證明。
對於總體而言,通常用μ表示總體平均數,有限總體的平均數為:
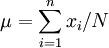
式中,N表示總體所包含的個體數。
當一個統計量的數學期望等於所估計的總體參數時,則稱此統計量為該總體參數的無偏估計量。統計學中常用樣本平均數( )作為總體平均數(μ)的估計量,並已證明樣本平均數 是總體平均數μ的無偏估計量。
)作為總體平均數(μ)的估計量,並已證明樣本平均數 是總體平均數μ的無偏估計量。
平均數主要包括有算術平均數(arithmetic mean)、中位數(median)、眾數(mode)、幾何平均數(geometric mean)及調和平均數(harmonic mean)。
1、算術平均數(arithmetic mean)
算術平均數是指資料中各觀測值的總和除以觀測值個數所得的商,簡稱平均數或均數,記為 。
。
2、中位數(median)
中位數是指將數據按大小順序排列起來,形成一個數列,居於數列中間位置的那個數據。中位數用Me表示。
從中位數的定義可知,所研究的數據中有一半小於中位數,一半大於中位數。中位數的作用與算術平均數相近,也是作為所研究數據的代表值。在一個等差數列或一個正態分佈數列中,中位數就等於算術平均數。
在數列中出現了極端變數值的情況下,用中位數作為代表值要比用算術平均數更好,因為中位數不受極端變數值的影響;如果研究目的就是為了反映中間水平,當然也應該用中位數。在統計數據的處理和分析時,可結合使用中位數。
3、眾數(mode)
眾數是指一組數據中出現次數最多的那個數據,一組數據可以有多個眾數,也可以沒有眾數。
4、幾何平均數(geometric mean)
幾何平均數是n個變數值連乘積的n次方根。
幾何平均數多用於計算平均比率和平均速度。如:平均利率、平均發展速度、平均合格率等。
5、調和平均數(harmonic mean)
調和平均數又稱倒數平均數,是變數倒數的算術平均數的倒數。
- ↑ 陳珍珍,羅樂勤.統計學〔M〕.廈門:廈門大學出版社,2002.4~5








謝謝!