眾數
出自 MBA智库百科(https://wiki.mbalib.com/)
眾數(Mode)
目錄 |
眾數是指一組數據中出現次數最多的那個數據,一組數據可以有多個眾數,也可以沒有眾數。眾數是由英國統計學家皮爾生首先提出來的。所謂眾數是指社會經濟現象中最普遍出現的標誌值。從分佈角度看,眾數是具有明顯集中趨勢的數值。
例如:某製鞋廠要瞭解消費者最需要哪種型號的男皮鞋,調查了某百貨商場某季度男皮鞋的銷售情況,得到資料如下表(某商場某季度男皮鞋銷售情況):
| 男皮鞋號碼/釐米 | 銷售量/雙 |
|---|---|
| 24.0 | 12 |
| 24.5 | 84 |
| 25.0 | 118 |
| 25.5 | 541 |
| 26.0 | 320 |
| 26.5 | 104 |
| 27.0 | 52 |
| 合計 | 1200 |
從表中可以看到,25.5釐米的鞋號銷售量最多,如果我們計算算術平均數,則平均號碼為25.65釐米,而這個號碼顯然是沒有實際意義的,而直接用25.5釐米作為顧客對男皮鞋所需尺寸的集中趨勢既便捷又符合實際。
統計上把這種在一組數據中出現次數最多的變數值叫做眾數。用Mo表示。它主要用於定類(品質標誌)數據的集中趨勢,當然也適用於作為定序(品質標誌)數據以及定距和定比(數量標誌)數據集中趨勢的測度值。上面的例子中,鞋號25.5釐米就是眾數。
1、眾數是以它在所有標誌值中所處的位置確定的全體單位標誌值的代表值,它不受分佈數列的極大或極小值的影響,從而增強了眾數對分佈數列的代表性。
2、當分組數列沒有任何一組的次數占多數,也即分佈數列中沒有明顯的集中趨勢,而是近似於均勻分佈時,則該次數分配數列無眾數。若將無眾數的分佈數列重新分組或各組頻數依序合併,又會使分配數列再現出明顯的集中趨勢。
3、如果與眾數組相比鄰的上下兩組的次數相等,則眾數組的組中值就是眾數值;如果與眾數組比鄰的上一組的次數較多,而下一組的次數較少,則眾數在眾數組內會偏向該組下限;如果與眾數組比鄰的上一組的次數較少,而下一組的次數較多,則眾數在眾數組內會偏向該組上限。
4、缺乏敏感性。這是由於眾數的計算只利用了眾數組的數據信息,不象數值平均數那樣利用了全部數據信息。
眾數的意義[1]
第一,眾數是一組數據中出現次數最多的數據,是一組數據中的原數據,而不是相應的次數。
第二,一組數據中的眾數可能不存在。
第三,眾數粗糙,但眾數不受個別數據的影響,可在數據缺陷較大或需要快速而粗略地尋求一組數據的代表值時用。
眾數的計算[2]
由品質數列和單項式變數數列確定眾數比較容易,哪個變數值出現的次數最多,它就是眾數,如上面的兩個例子。
若所掌握的資料是組距式數列,則只能按一定的方法來推算眾數的近似值。計算公式為:
式中:
- L——眾數所在組下限;
- U——眾數所在組上限;
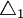 ——眾數所在組次數與其下限的鄰組次數之差;
——眾數所在組次數與其下限的鄰組次數之差;
 ——眾數所在組次數與其上限的鄰組次數之差;
——眾數所在組次數與其上限的鄰組次數之差;
- d——眾數所在組組距。
例:根據下表的數據,計算50名工人日加工零件數的眾數。
解:從表中的數據可以看出,最大的頻數值是14,即眾數組為120~125這一組,根據公式得50名工人日加工零件的眾數為:
 (件)
(件)
或: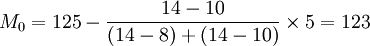 (件)
(件)
眾數是一種位置平均數,是總體中出現次數最多的變數值,因而在實際工作中有時有它特殊的用途。諸如,要說明一個企業中工人最普遍的技術等級,說明消費者需要的內衣、鞋襪、帽子等最普遍的號碼,說明農貿市場上某種農副產品最普遍的成交價格等,都需要利用眾數。但是必須註意,從分佈的角度看,眾數是具有明顯集中趨勢點的數值,一組數據分佈的最高峰點所對應的數值即為眾數。當然,如果數據的分佈沒有明顯的集中趨勢或最高峰點,眾數也可能不存在;如果有兩個最高峰點,也可以有兩個眾數。只有在總體單位比較多,而且又明顯地集中於某個變數值時,計算眾數才有意義。
評論(共49條)
你能告訴我6、6、8、8有眾數嗎?
有的,這種情況下,2和8都是眾數。
眾數著眼於對各數據出現的次數的考察, 是一組數據中的原數據,其大小隻與這組數據中的部分數據有關,當一組數據中有不少數據多次重覆出現時,其眾數往往是我們關心的一種統計量。註意:一組數據中的眾數有時不只一個,如數據2、3、-1、2、l、3中,2和3都出現了2次,它們都是這組數據的眾數。
1,1,2,2,3,3,4,4,5,5,中有眾數嗎 謝謝
沒有眾數,這列數中每個數字出現的次數都是一樣的。
但是,如果有兩個或兩個以上個數出現次數都是最多的,那麼這幾個數都是這組數據的眾數。
例如:1,2,2,3,3,4的眾數是2和3。
一組數據可能沒有眾數或有幾個眾數。
數列 2 3 3 4 1 5 3 2 4 3 6的眾數是
眾數是3
眾數是指一組數據中出現次數最多的那個數據
根據頻數大小來確定眾數所在組是不是不太科學啊! 比如:例中頻數為10的那一組,即125~130組,如果其中每個元素都恰好是127,即正好有10名工人日加工零件數為127件,則眾數應該為127,而不是公式算出來的123。公式根據頻數最大就確定眾數所在組應該是錯誤的吧!
如果一組數據中,所有數據都是一樣的,比方說6,6,6,6,6,6,6,6,那這組數據有眾數嗎?
6就是眾數的哦~
如果所有數據出現的次數都一樣,那麼這組數據沒有眾數。 例如:1,2,3,4,5沒有眾數。
如果一組數據中,所有數據都是一樣的,比方說6,6,6,6,6,6,6,6,那這組數據有眾數嗎? 懇請專業人士回答,謝謝!
如果一組數據中,所有數據都是一樣的,比方說6,6,6,6,6,6,6,6,那這組數據有眾數嗎? 懇請專業人士回答,謝謝!
根據眾數的意義以及使用範圍,以及本篇最後一段文字里的“如果數據的分佈沒有明顯的集中趨勢或最高峰點,眾數也可能不存在”,可以判斷出,你給的這組都是6的數據,是沒有計算眾數的意義的。所以,眾數不存在。
1,1,2,2,3,3,4,4,5,5有眾數嗎?
有,是3!
有,是6
數列 2 3 3 4 1 5 3 2 4 3 6的眾數是
4
1,1,2,2,3,3,4,4,5,5有眾數嗎?
次數皆一樣多,眾數不存在
沒有眾數,這列數中每個數字出現的次數都是一樣的。
當分組數列沒有任何一組的次數占多數,也即分佈數列中沒有明顯的集中趨勢,而是近似於均勻分佈時,則該次數分配數列無眾數。若將無眾數的分佈數列重新分組或各組頻數依序合併,又會使分配數列再現出明顯的集中趨勢。但是,如果有兩個或兩個以上個數出現次數都是最多的,那麼這幾個數都是這組數據的眾數。
你能告訴我6、6、8、8有眾數嗎?
6, 6, 8, 8的眾數應該是7
沒有,“如果數據的分佈沒有明顯的集中趨勢或最高峰點,眾數也可能不存在;”6,6,8,8沒有“最”,所以這組數據沒有眾數!
你能告訴我6、6、8、8有眾數嗎?
沒有眾數,眾數具有2個存在的前提:總體單位量相當大;次數分佈具有明顯集中趨勢。顯然,你給出的數據都不滿足兩點,眾數不存在。

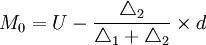








你能告訴我6、6、8、8有眾數嗎?