集中趨勢
出自 MBA智库百科(https://wiki.mbalib.com/)
集中趨勢(central tendency)
目錄 |
什麼是集中趨勢[1]
集中趨勢是指頻數分佈數列中備觀察值有一種向中心集中的趨勢,在中心附近的觀察值數目較多,遠離中心的較少。
集中趨勢的概述[1]
集中趨勢所反映的是一組資料中各種數據所具有的共同趨勢,即資料的各種數據所集聚的位置。因此,它是對變數數列進行分析的首要指標,它往往作為總體的代表水平同其他與之同質的總體進行比較。
集中趨勢常用指標[2]
其中也包括市場經濟變化發展,其常用指標數有平均數、中位數和眾數三類。
1.平均數
平均數是測定集中趨勢的一種常用特征數 主要用於分析所研究對象在不同時空和歷史條件下的各種事物變化發展的水平.其中也包括市場經濟。常見的平均數有算術平均數、加權平均數、幾何平均數三種。
(1)算術平均數
算術平均數是指用於反映一組同質觀測值的平均水平.適用於正態或近似正態分佈的變數數據。若所得的數據較少且沒有分組時,一般採用算術平均數演算法.即只需要將所有數據相加 除以其個數,這也就是在日常生活中常說的平均值。
若遇到的數據是分組的.且各組數據重覆出現過一定的數次(即頻數)則用上述演算法根本解決不了.若要計算其平均數必須用加權平均數演算法來完成。
(2)加權平均數
加權平均數是指含有不同頻數數據的平均數 它是把原始數據按照合理的頻數來計算的,計算公式為
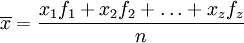 。
。
式中n為總次數,f為組的頻數。
(3)幾何平均數
幾何平均數是指n個數值連乘的n次方根。在計算社會經濟問題的平均發展速度方面具有很重要的作用,主要適用於經濟現象的總比率是若幹個比率的連乘積,或經濟現象的總發展速度是各時期經濟發展速度的連乘積時,計算經濟發展的平均比率或平均速度。計算公式為:
![\overline{x}\sqrt[n]{x_1x_2\ldots x_n}](/w/images/math/5/2/3/523f32acc2825da32d2bb7aa2da20418.png)
式中x_n為第n個數值,n為個數。
2.中位數
中位數是指將一組數據按大小順序排列起來,處於中間位置的那個數。中位數一般用來表示社會經濟現象集中趨勢的一般水平。而中位數的計算,根據數據的不同可分為以下兩種情況:
(1)未分組。首先把沒有分組的數據按大小順序排列,然後運用公式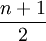 求中位數所在位置,處於該位置的數就是中位數。當n為奇數時.則居中間位置上的那個數就是中位數 當n為偶數時,居中間位置上就有兩個數,此時的中位數就是這兩個數的算術平均數。
求中位數所在位置,處於該位置的數就是中位數。當n為奇數時.則居中間位置上的那個數就是中位數 當n為偶數時,居中間位置上就有兩個數,此時的中位數就是這兩個數的算術平均數。
(2)分組。首先要根據算術平均數演算法確定出中位數所在的組別,然後運用內插法計算中位數的近似值。由於這種情況出現較少且求難度較大,在此就不介紹。
3.眾數
眾數是指將一組數據按大小順序排列出現次數最多的那個數值,通常通過觀察法直接得到。
以上介紹的三種指標數雖然反映的都是事物變化發展的一般水平和總體趨勢,但要註意的是平均數作為一組數據的代表。比較可靠和穩定,它與這組數據中的每一個數都有關係 對這些數據所包含的信息的反映最為充分,因而應用最為廣泛。尤其在市場經濟方面,但計算較繁瑣,並且易受極端數據的影響。而中位數和眾數則不同,它們的可靠性較差,但不受極端數據的影響。若組中個別數據變動較大時 使用眾數來表示這組數據的集中趨勢效果更佳。
案例一:集中趨勢在市場經濟管理中的應用[2]
由於集中趨勢代表的事物變化發展的一般水平和總體趨勢,在市場經濟管理中,經常運用它可解決兩個方面的問題。
1.市場經濟變化的平均速度
在市場經濟管理中經常遇到如此情況,如瞭解某小區居民的每月生活消費情況。由於不同的家庭經濟條件,那麼每月的生活消費也就不同。若要瞭解小區居民的每月平均生活消費情況,一般只能通過抽查方式進行,先抽查一定數量的各式家庭(即經濟條件好、中和差的三種家庭),得到他們的每月生活消費數據,然後算出每月生活消費的平均值,即得到整個小區居民每月的平均生活消費情況。
由於生活消費的水平高低不同,那麼就涉及到分組,若要求其平均數,一般只能採用加權平均數演算法來求,表格中的戶數即為頻數。如隨機抽查了該小區2O戶家庭的生活消費情況,抽查結果如下:
| 月消費(元) | 500 | 600 | 700 | 1000 | 1200 |
| 戶數 | 4 | 4 | 7 | 3 | 2 |
根據加權平均數演算法,則可得整個小區居民每月的平均生活消費情況為
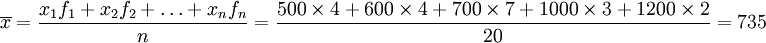 (元)
(元)
另外,在看電視或閱讀經濟方面的書刊、雜誌時經常會遇見類似的問題,如知道了某地區的某些時間段的經濟增長情況,但要計算該地區經濟平均增長速度。針對此類問題,有不少人可能會直接通過算術平均數演算法來計算該地區的平均增長速度,但是他們沒有考慮到某段時間經濟增長是在前一段期間的基礎進行,因此對於此問題應該用幾何平均數演算法來解決。例如,若某地區5年來的國民生產總值年增長速度分別為7%,8%,1O%,12%,18%。若要瞭解5年來的該地區的平均增長速度。根據上述分析,應先用幾何平均數演算法來計算每年的平均增長率,再將所得值減少1,即可得平均增長速度。5年來的平均增長率為![\overline{x}=\sqrt[5]{1.07\times1.08\times1.10\times1.12\times1.18}=11.093](/w/images/math/4/b/e/4be3c855c4541d504fd01fae521d67ce.png) ,那麼5年來的平均增長速度為10.93%。
,那麼5年來的平均增長速度為10.93%。
2.判斷同類產品的質量
在現實的經濟環境中,有些商家往往抓住消費者對經濟知識的熟悉性,做一些文字游戲,以次充好,來欺騙消費者。如甲、乙、丙三家家電廠在廣告中聲稱,他們謀種電子產品在正常情況下的使用壽命均為8年,註意這個正常情況下的使用壽命指的是平均使用壽命,但質量檢測部門對這三家銷售的產品的使用進行跟蹤調查,得到下列結果(單位:年)
| 甲廠 | 4 | 5 | 5 | 5 | 7 | 9 | 12 | 13 | 15 | |
| 乙廠 | 6 | 6 | 8 | 8 | 12 | 9 | 10 | 8 | 14 | 15 |
| 丙廠 | 4 | 7 | 4 | 6 | 4 | 9 | 13 | 16 | 15 | 16 |
對於一般人來說,看到三家家電廠的廣告詞後,就會認為它們的產品質量是一樣好的,但從質量檢測部門跟蹤調查數據來看,發現它們的產品質量不一樣,說明廣告詞有問題,但對一般人來說,無從說明。而對熟悉集中趨勢方面知識的人來說,這個問題就很容易了。從質量檢測部門的數據來看,對於甲廠電子產品在正常情況下的使用壽命8竿,它指的是電子產品使用壽命的平均數,演算法為
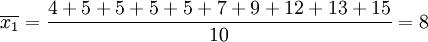 (年)
(年)
對於乙廠電子產品在正常情況下的使用壽命8竿,它指的是電子產品使用壽命的眾數。根據眾數的演算法,先將該組數據按從小到大排序,得序列6,6,8,8,8,9,10,12,14,15,從序列中可看出,在此組數中8有3個6有2個9、10、12、14、15各1個,故8是眾數,二乙廠產品的平均壽命是。
 (年)
(年)
對於丙廠電子產品在正常情況下的使用壽命8年,它指的是產品使用壽命的中位數,根據中位數的演算法,先將該組數據按從小到大排序,分別是4,4,4,6,7,9,13,15,16,16,由於該組又10個數據,由於10是偶數,根據中位數演算法,中位數應為 ,但該廠產品的平均壽命是。
,但該廠產品的平均壽命是。
 (年)
(年)
從上述分析可知,雖然三家廠在廣告中都說電子產品的使用壽命均為8年,但電子產品的真正平均使用壽命分別為8年、9.6年和9.4年,由此可得出乙廠的電子產品的質量最好,丙廠其次,甲廠最差,通過它就可以判斷同類產品的產品質量的好壞。
上式中x_1——甲;
x_2——乙;
x_3——丙。
總之,通過以上分析可知,利用集中趨勢可解決市場經濟環境中的平均變化率和產品質量好壞的一些問題,這些問題看起來簡單,但又很容易讓大家忽視的,若要瞭解清楚明白,最好學一些統計分析方面知識,使自己今後在市場經濟管理中立於不敗之地。








還有分位數吧