中位數
出自 MBA智库百科(https://wiki.mbalib.com/)
中位數(Median)
中位數(Median)又稱中值,統計學中的專有名詞,是按順序排列的一組數據中居於中間位置的數,代表一個樣本、種群或概率分佈中的一個數值,其可將數值集合劃分為相等的上下兩部分。對於有限的數集,可以通過把所有觀察值高低排序後找出正中間的一個作為中位數。如果觀察值有偶數個,通常取最中間的兩個數值的平均數作為中位數。
目錄 |
中位數是指將數據按大小順序排列起來,形成一個數列,居於數列中間位置的那個數據。中位數用Me表示。
從中位數的定義可知,所研究的數據中有一半小於中位數,一半大於中位數。中位數的作用與算術平均數相近,也是作為所研究數據的代表值。在一個等差數列或一個正態分佈數列中,中位數就等於算術平均數。
在數列中出現了極端變數值的情況下,用中位數作為代表值要比用算術平均數更好,因為中位數不受極端變數值的影響;如果研究目的就是為了反映中間水平,當然也應該用中位數。在統計數據的處理和分析時,可結合使用中位數。
確定中位數,必須將總體各單位的標誌值按大小順序排列,最好是編製出變數數列。這裡有兩種情況:
1、對於未分組的原始資料,首先必須將標誌值按大小排序。設排序的結果為:
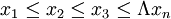
則中位數就可以按下麵的方式確定:
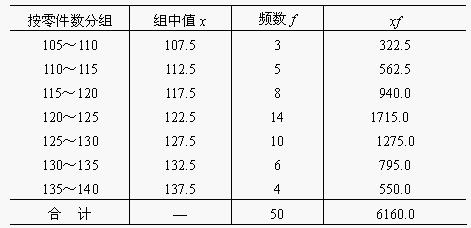
例如,根據下表的數據,計算50名工人日加工零件數的中位數。
中位數的位置在(50+1)/2 = 25.5,中位數在第25個數值(123)和第26個數值(123)之間,即Me = (123+123)/2=123(件)。
2、由分組資料確定中位數
由組距數列確定中位數,應先按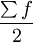 的公式求出中位數所在組的位置,然後再按下限公式或上限公式確定中位數。
的公式求出中位數所在組的位置,然後再按下限公式或上限公式確定中位數。
下限公式:
上限公式: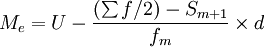
式中:
- Me——中位數;
- L——中位數所在組下限;
- U——中位數所在組上限;
- fm——為中位數所在組的次數;
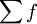 ——總次數;
——總次數;
- d——中位數所在組的組距;
- Sm − 1——中位數所在組以下的累計次數;
- Sm + 1——中位數所在組以上的累計次數。
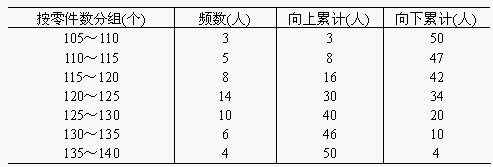
例:根據上面例表的數據,計算50名工人日加工零件數的中位數。
解(某企業50名工人加工零件中位數計算表):
由上表可知,中位數的位置=50/2=25,即中位數在120~125這一組,L=120,Sm − 1 = 16,U=125,Sm + 1 = 20,fm = 14,d=5,根據中位數公式得:
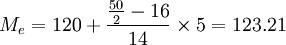 (件)
(件)
或 (件)
(件)
1、中位數是以它在所有標誌值中所處的位置確定的全體單位標誌值的代表值,不受分佈數列的極大或極小值影響,從而在一定程度上提高了中位數對分佈數列的代表性。
2、有些離散型變數的單項式數列,當次數分佈偏態時,中位數的代表性會受到影響。
3、缺乏敏感性。
1)平均數是通過計算得到的,因此它會因每一個數據的變化而變化。
2)中位數是通過排序得到的,它不受最大、最小兩個極端數值的影響。部分數據的變動對中位數沒有影響,當一組數據中的個別數據變動較大時,常用它來描述這組數據的集中趨勢。
3)眾數也是數據的一種代表數,反映了一組數據的集中程度.日常生活中諸如“最佳”、“最受歡迎”、“最滿意”等,都與眾數有關係,它反映了一種最普遍的傾向。
優缺點:
平均數:需要全組所有數據來計算;易受數據中極端數值的影響。中位數:僅需把數據按順序排列後即可確定;不易受數據中極端數值的影響。眾數:通過計數得到;不易受數據中極端數值的影響。
評論(共18條)
想問那個中位數位置算出來後,即50÷2=25,然後是怎麼知道它在哪一組的?是看它接近於30,而不是16麽?如果兩邊一樣接近呢?
想問那個中位數位置算出來後,即50÷2=25,然後是怎麼知道它在哪一組的?是看它接近於30,而不是16麽?如果兩邊一樣接近呢?
一般嚴格考試的時候,會明確告訴分段是≥或者是≤,一般沒有給,會預設是≤。比如以50為一段,就是50≤x<100;100≤x<150;150≤x<200...所以,25≤x<35,而不是落在15≤x<25的區間。謝謝
想問那個中位數位置算出來後,即50÷2=25,然後是怎麼知道它在哪一組的?是看它接近於30,而不是16麽?如果兩邊一樣接近呢?
在頻數25位和26位上求中位數,而25,26為的頻數就分佈在120~125上
1,1,10,10,10;這5個數的中位數是10?
對
1,1,10,10,10;這5個數的中位數是10?
你只有兩個數,就補存在中位數。
1,1,10,10,10;這5個數的中位數是10?
是的
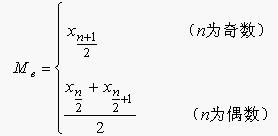








謝謝