中位数
出自 MBA智库百科(https://wiki.mbalib.com/)
中位数(Median)
中位数(Median)又称中值,统计学中的专有名词,是按顺序排列的一组数据中居于中间位置的数,代表一个样本、种群或概率分布中的一个数值,其可将数值集合划分为相等的上下两部分。对于有限的数集,可以通过把所有观察值高低排序后找出正中间的一个作为中位数。如果观察值有偶数个,通常取最中间的两个数值的平均数作为中位数。
目录 |
中位数是指将数据按大小顺序排列起来,形成一个数列,居于数列中间位置的那个数据。中位数用Me表示。
从中位数的定义可知,所研究的数据中有一半小于中位数,一半大于中位数。中位数的作用与算术平均数相近,也是作为所研究数据的代表值。在一个等差数列或一个正态分布数列中,中位数就等于算术平均数。
在数列中出现了极端变量值的情况下,用中位数作为代表值要比用算术平均数更好,因为中位数不受极端变量值的影响;如果研究目的就是为了反映中间水平,当然也应该用中位数。在统计数据的处理和分析时,可结合使用中位数。
确定中位数,必须将总体各单位的标志值按大小顺序排列,最好是编制出变量数列。这里有两种情况:
1、对于未分组的原始资料,首先必须将标志值按大小排序。设排序的结果为:
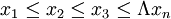
则中位数就可以按下面的方式确定:
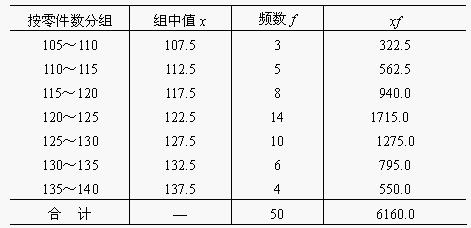
例如,根据下表的数据,计算50名工人日加工零件数的中位数。
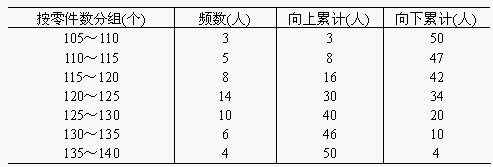
中位数的位置在(50+1)/2 = 25.5,中位数在第25个数值(123)和第26个数值(123)之间,即Me = (123+123)/2=123(件)。
2、由分组资料确定中位数
由组距数列确定中位数,应先按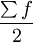 的公式求出中位数所在组的位置,然后再按下限公式或上限公式确定中位数。
的公式求出中位数所在组的位置,然后再按下限公式或上限公式确定中位数。
下限公式:
上限公式: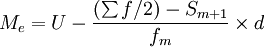
式中:
- Me——中位数;
- L——中位数所在组下限;
- U——中位数所在组上限;
- fm——为中位数所在组的次数;
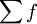 ——总次数;
——总次数;
- d——中位数所在组的组距;
- Sm − 1——中位数所在组以下的累计次数;
- Sm + 1——中位数所在组以上的累计次数。
例:根据上面例表的数据,计算50名工人日加工零件数的中位数。
解(某企业50名工人加工零件中位数计算表):
由上表可知,中位数的位置=50/2=25,即中位数在120~125这一组,L=120,Sm − 1 = 16,U=125,Sm + 1 = 20,fm = 14,d=5,根据中位数公式得:
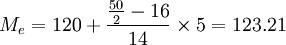 (件)
(件)
或 (件)
(件)
1、中位数是以它在所有标志值中所处的位置确定的全体单位标志值的代表值,不受分布数列的极大或极小值影响,从而在一定程度上提高了中位数对分布数列的代表性。
2、有些离散型变量的单项式数列,当次数分布偏态时,中位数的代表性会受到影响。
3、缺乏敏感性。
1)平均数是通过计算得到的,因此它会因每一个数据的变化而变化。
2)中位数是通过排序得到的,它不受最大、最小两个极端数值的影响。部分数据的变动对中位数没有影响,当一组数据中的个别数据变动较大时,常用它来描述这组数据的集中趋势。
3)众数也是数据的一种代表数,反映了一组数据的集中程度.日常生活中诸如“最佳”、“最受欢迎”、“最满意”等,都与众数有关系,它反映了一种最普遍的倾向。
优缺点:
平均数:需要全组所有数据来计算;易受数据中极端数值的影响。中位数:仅需把数据按顺序排列后即可确定;不易受数据中极端数值的影响。众数:通过计数得到;不易受数据中极端数值的影响。
评论(共18条)
想问那个中位数位置算出来后,即50÷2=25,然后是怎么知道它在哪一组的?是看它接近于30,而不是16么?如果两边一样接近呢?
想问那个中位数位置算出来后,即50÷2=25,然后是怎么知道它在哪一组的?是看它接近于30,而不是16么?如果两边一样接近呢?
一般严格考试的时候,会明确告诉分段是≥或者是≤,一般没有给,会默认是≤。比如以50为一段,就是50≤x<100;100≤x<150;150≤x<200...所以,25≤x<35,而不是落在15≤x<25的区间。谢谢
想问那个中位数位置算出来后,即50÷2=25,然后是怎么知道它在哪一组的?是看它接近于30,而不是16么?如果两边一样接近呢?
在频数25位和26位上求中位数,而25,26为的频数就分布在120~125上
1,1,10,10,10;这5个数的中位数是10?
对
1,1,10,10,10;这5个数的中位数是10?
你只有两个数,就补存在中位数。
1,1,10,10,10;这5个数的中位数是10?
是的
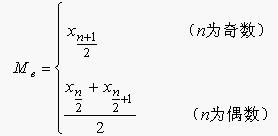








谢谢