隨機誤差
出自 MBA智库百科(https://wiki.mbalib.com/)
隨機誤差(Random error)
目錄 |
什麼是隨機誤差[1]
隨機誤差也稱為偶然誤差和不定誤差,是由於在測定過程中一系列有關因素微小的隨機波動而形成的具有相互抵償性的誤差。
它的特點:大小和方向都不固定,也無法測量或校正。隨機誤差的性質是:隨著測定次數的增加,正負誤差可以相互抵償,誤差的平均值將逐漸趨向於零。
隨機誤差的原因[1]
產生隨機誤差的原因有許多。例如,在測量過程中由於溫度、濕度以及灰塵等的影響都可能引起數據的波動。再比如在讀取滴定管數據時,估計的小數點後第二位的數值,幾次讀數不一致。這類誤差在操作中不能完全避免。
隨機誤差的大小、正負在同一個實驗室中不是恆定的,並很難找到產生的確切原因,所以又稱不定誤差。
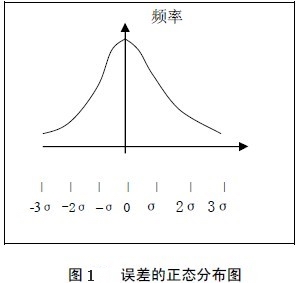
從錶面上看,它的出現似乎沒有規律,即在單次測定過程中,其大小及符號無法預言,沒有任何規律性,具有非單向性的特點。但是,如果進行反覆多次測定,就會發現隨機誤差的出現還是有一定的規律的,即具有統計規律性。總的來說,大小相等的正、負誤差出現的幾率相等,小誤差出現的機會多,大誤差出現的機會少,特大的正、負誤差出現的機會更小。這一規律可以用正態分佈曲線(圖1)表示。[1]
圖中橫軸代表誤差的大小,以總體標準差σ為單位,縱軸代表誤差發生的頻率。
隨機誤差是由隨機因素引起的,可大可小,可正可負,粗看起來,無規律可循,但經過大量實驗可以發現,隨機誤差的分佈也有一定規律性:
1、大小相近的正誤差和負誤差出現的機率相等,即絕對值相近 ( 或相等 ) 而符號相反的誤差以同等的機率出現。
2、小誤差出現的頻率高,而大誤差出現的頻數較低,很大誤差出現的機率近於零或極少。即:偶然誤差的規律符合正態分佈。在消除系統誤差的情況下,增加測定次數,取其平均值,可減少偶然誤差。實際工作中測定次數為4~6次已經足夠了。一般情況下,很少有超過4次平行測定的。
隨機誤差的註意點[1]
應該指出的是,系統誤差與隨機誤差的劃分也不是絕對的,有時很難區分某種誤差是系統誤差還是隨機誤差。例如判斷滴定終點的遲早、觀察顏色的深淺,總有一定的隨機性。
另外,有些因素在短時間內引起的誤差可能屬於隨機誤差,但在一個較長的時期內就可能轉化為系統誤差。例如,溫度的影響,在某一天或幾天時間內進行測量時,它的波動所引起的誤差應屬於隨機誤差,可是在某一季節較長時間內,它的影響所造成的誤差就可以劃為系統誤差。
除此之外,不同的操作方法,誤差的性質也有所不同。例如對於具有分刻度的吸量管,不同的吸量管誤差可能是各不相同的。如果用幾支吸量管吸取相同體積同一溶液,所產生的誤差屬於隨機誤差;如果只用一隻吸量管,幾次吸取相同體積的同一溶液,造成的誤差則應屬於系統誤差;但是,如果每次吸取溶液時使用不同的刻度區,由於不同刻度區的誤差可能有大有小,有正有負,這時產生的誤差就轉化為隨機誤差。
除了以上兩類誤差外,在測定過程中,由於操作者粗心大意或不按操作規程辦事而造成的測定過程中溶液的濺失、加錯試劑、看錯刻度、記錄錯誤,以及儀器測量參數設置錯誤等等,都屬於過失誤差,會對計量或測定結果帶來嚴重影響,必須註意避免。為此,必須嚴格遵守操作規程,一絲不苟,耐心細緻的進行實驗,在學習過程中養成良好的實驗習慣。








真正的無規律性的誤差,才能在某一個變數上具有正態分佈的性質。