總體標準差

出自 MBA智库百科(https://wiki.mbalib.com/)

總體標準差（population standard deviation ）

　　總體標準差是反映研究總體內個體之間差異程度的一種統計指標，用σ表示。

　　總體方差是一組資料中各數值與其算術平均數離差平方和的平均數。總體標準差則是總體方差的平方根。

　　標準差是最常用和最重要的變異性測量。標準差以分佈的平均數作為參照點，用考慮每個數據和平均 數之間的距離來測量變異性。它由數據是否接近或遠離平均數來決定。也就是說，它考慮數據是聚集還是離散的？簡單來說，標準差與數據到平均數的平均距離近似。

　　方差被定義為平方差的平均數。這個平均數為總和除以N，因此，總體方差的公式為：

　　方差=

　　標準差是方差的平方根，因此，總體標準差的公式為：

　　標準差=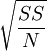

　　與平均數（μ）一樣，方差和標準差是總體的參數，將用希臘字母表示。我們用σ表示總體標準差。為了強調標準差和方差之間的關係，我們用σ²表示總體方差。所以：

　　總體標準差=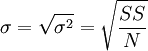

　　總體方差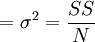

　　總體參數中除了均值和比例的估計之外，還經常要對差異的情況作出估計，例如：一架飛機的電纜如果發生斷裂，飛機就會失去控制，因而嚴格控制其質量非常必要。但只知道電纜的平均強度是否達到標準是不夠的，因為如果電纜差異太大，電纜強度太強，都容易發生斷裂，後果不堪設想。所以對於電纜強度質量不僅應知道均值，而且還應知道方差，即需要要對電纜的方差進行估計。

　　對方差進行估計要用到Excel中的卡方分佈反函數CHIINV。若已知總體方差σ²（總體方差未知時用樣本方差S²代替總體方差）和樣本數，對於給定的顯著性水平σ，利用CHINV函數可以求出臨界值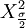和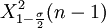,則總體方差σd的置信度為1 − σ的置信區間為

（)。

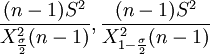其中，和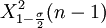

分別是自由度為n − 1的X²分佈的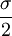和的水平的分位数。

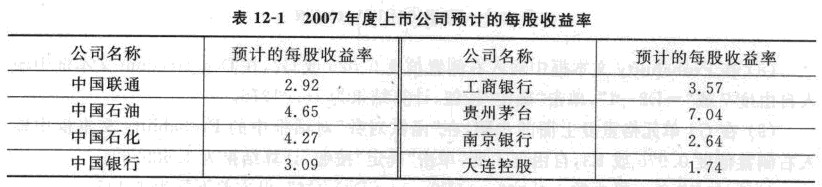
　　假设上市公司预计的每股收益率服从正态分布，现有8个公司组成一个简单随机样本，2007年的有关数据如表12-1所示，试建立总体标准差的95%的置信区间。

　　设随机变量X表示预计的每股收益率，则由已知条件知X～N（μ,σ²）,且σ²未知。具体操作步骤如下：

　　（1）打开“《大学计算机应用高级教程》教学资源\第3篇Excel数据分析与处理\第12章 参数估计与分析\第12章 参数估计与分析.xls”工作簿，选定“例12-10方程估计”工作表。

　　（2）将表12-1中的数据输入“方差估计工作表的相关单元格中，输入后的工作表如图12-20所示”

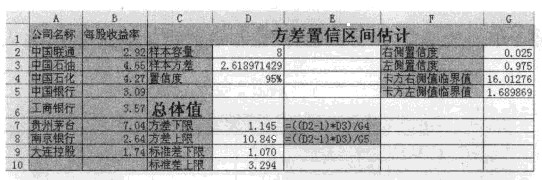
　　（3）在D2单元格中输入样本容量的值8：在D3单元格计算样本方差得值2.618971。

　　（4）在D4单元格中输入置信度95%。

　　（5）在G2单元格中输入右侧置信度0.025：在G3但与昂输入左侧置信度0.975。

　　说明：通常卡方分布函数所给出的是由右侧向左侧累加的概率。若置信度为95%，则右侧临界值的右侧面积称为右侧置信度，为0.025，左侧临界值的右侧面积为左侧置信度，它等于中心面积加上右侧置信度，即左侧置信度=0.95+0.025=03975。

　　（6）选定G4单元格，依次选择“插入”→“函数”命令，打开“插入函数”对话框。

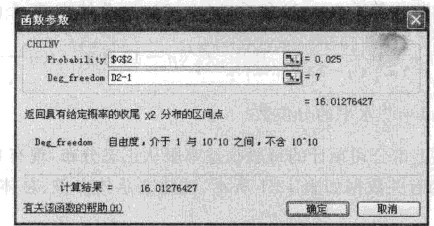
　　（7）在“函数分类”列表中选择“统计”选项，在“函数名”列表中选择CHIINV选项，单击“确定”按钮，打开“函数参数”对话框，如图所示。

　　（8）在Probability文本框中输入右侧置信度0.025或G2，在Deg_freedom文本框中输入自由度7或“=D2-1”，单击“确定”按钮，计算结果为16.01276。

　　（9）在G4单元格重复上面的步骤，在“函数对数”对话框中的Probability文本框中输入右侧置信度0.975或E3，自由度不变，单击“确定”按钮，计算结果为1.689869。

　　（10）在D7单元格中输入公式“=（（D2-1）*D3）/G4”，得方差下限为1.145。

　　（11）在D8单元格中输入公司“=（（D2-1）*D3）/G5”，得方差上限为10.849。

　　（12）在D9和D10单元格中分别对D7和D8单元格开平方，即在D9单元格中输入公式“=SQRT(D7)”,按Enter键得1.070，在D10单元格输入公式“=SQRT(D8)”,按Enter键得3.294。结果如图所示。

　　故总体方差的95%的置信区间为（1.145，10.849），总体标准差的95%的置信区间为（1.070，3.294）。

　　由此我们有95%的把握认为这些上市公司整体每股收益率的浮动范围在1.070～3.294之间。

• 标准误差
• 标准差