樣本容量
出自 MBA智库百科(https://wiki.mbalib.com/)
樣本容量(sample size)
目錄 |
樣本容量又稱“樣本數”。指一個樣本的必要抽樣單位數目。在組織抽樣調查時,抽樣誤差的大小直接影響樣本指標代表性的大小,而必要的樣本單位數目是保證抽樣誤差不超過某一給定範圍的重要因素之一。因此,在抽樣設計時,必須決定樣本單位數目,因為適當的樣本單位數目是保證樣本指標具有充分代表性的基本前提。
樣本是從總體中抽出的部分單位集合,這個集合的大小就叫做樣本量。一般來說,樣本的容量大的話,樣本的誤差就小。反之則大。通常樣本單位數大於30的樣本可稱為大樣本,小於30的樣本則稱為小樣本。在實際應用中,我們應該根據調查的目的認真考慮樣本量的大小。
樣本容量的大小涉及到調研中所要包括的單元數。確定樣本容量的大小是比較複雜的問題,既要有定性的考慮也要有定量的考慮。從定性的方面考慮樣本量的大小,其考慮因素有:決策的重要性,調研的性質,變數個數,數據分析的性質,同類研究中所用的樣本量,發生率,完成率,資源限制等。具體地說,更重要的決策,需要更多的信息和更準確的信息,這就需要較大的樣本;探索性研究,樣本量一般較小,而結論性研究如描述性的調查,就需要較大的樣本;收集有關許多變數的數據,樣本量就要大一些,以減少抽樣誤差的累積效應;如果需要採用多元統計方法對數據進行複雜的高級分析,樣本量就應當較大;如果需要特別詳細的分析,如做許多分類等,也需要大樣本。針對子樣本分析比只限於對總樣本分析,所需樣本量要大得多。
所謂樣本個數,就是樣本可能的數目,指的是從一個總體中可能抽取的樣本數。例如一個大小為500的樣本,從中抽取100個做抽樣調查,則樣本個數為100。
具體確定樣本量還有相應的統計學公式,不同的抽樣方法對應不同的公式。根據樣本量計算公式,我們知道,樣本量的大小不取決於總體的多少,而取決於(1) 研究對象的變化程度;(2) 所要求或允許的誤差大小(即精度要求);(3) 要求推斷的置信程度。也就是說,當所研究的現象越複雜,差異越大時,樣本量要求越大;當要求的精度越高,可推斷性要求越高時,樣本量越大。因此,如果不同城市分別進行推斷時,大城市多抽,小城市少抽這種說法原則上是不對的。在大城市抽樣太大是浪費,在小城市抽樣太少沒有推斷價值。
總之,在確定抽樣方法和樣本量的時候,既要考慮調查的目的、調查性質和精度要求(抽樣誤差)等,又要考慮實際操作的可實施性,非抽樣誤差的控制、經費預算等。專業調查公司在這方面會根據您的情況及調查性質,進行綜合權衡,達到一個最優的樣本容量的選擇。
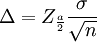
上式兩邊整理可得:
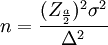
以上就是在給定極限誤差、概率誤差要求下,至少應抽取的樣本容量。
- 2.已知總體方差,不重覆抽樣條件下:
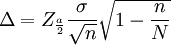
上式兩邊整理可得:

在以上公式中,各字母表示意義如下:
Z:概率度
N:樣本總數
n:樣本容量
a:極限誤差
- 1.重覆抽樣條件下:
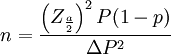
- 2.不重覆抽樣條件下:
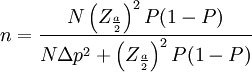
其中各字母的含義如下:
P:總體成數
p:樣本成數
一個箱子最多能放50個蘋果(樣本),從中取樣30個。
在這裡,蘋果是樣本,箱子最多能放的個數(即蘋果的總數)50是這個樣本的樣本(容)量,而所抽取的樣本個數30則是樣本量。








不重覆抽樣的分子少了一個N~