抽樣誤差

出自 MBA智库百科(https://wiki.mbalib.com/)

抽樣誤差（Sampling error）

　　在抽樣檢查中，由於用樣本指標代替全及指標所產生的誤差可分為兩種：一種是由於主觀因素破壞了隨機原則而產生的誤差，稱為系統性誤差；另一種是由於抽樣的隨機性引起的偶然的代表性誤差。抽樣誤差僅僅是指後一種由於抽樣的隨機性而帶來的偶然的代表性誤差，而不是指前一種因不遵循隨機性原則而造成的系統性誤差。

　　總的說來，抽樣誤差是指樣本指標與全及總體指標之間的絕對誤差。在進行抽樣檢查時不可避免會產生抽樣誤差，因為從總體中隨機抽取的樣本，其結構不可能和總體完全一致。例如樣本平均數與總體平均數之差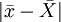，樣本成數與總體成數之差 | p − P | 。雖然抽樣誤差不可避免，但可以運用大數定律的數學公式加以精確地計算，確定它具體的數量界限，並可通過抽樣設計加以控制。

　　抽樣誤差也是衡量抽樣檢查準確程度的指標。抽樣誤差越大，表明抽樣總體對全及總體的代表性越小，抽樣檢查的結果越不可靠。反之，抽樣誤差越小，說明抽樣總體對全及總體的代表性越大，抽樣檢查的結果越準確可靠。在統計學中把抽樣誤差分為抽樣平均誤差和抽樣極限誤差，下麵就這兩種誤差分別進行闡釋。為使推理過程簡化，這裡不對屬性總體進行分析，而僅對變數總體進行分析計算。

　　1、表現形式：平均數指標抽樣誤差；成數（比重）抽樣誤差。

　　2、平均數指標的抽樣誤差

　　1）重覆抽樣的條件下：

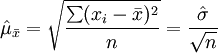
　　2)不重覆抽樣的條件下：

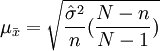
　　3、成數指標的抽樣誤差

　　1）重覆抽樣的條件下：

　　2）不重覆抽樣的條件下：

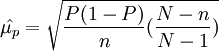
　　1.總體各單位標誌值的差異程度。差異程度愈大則抽樣誤差愈大，差異程度愈小則則抽樣誤差愈小。

　　2.樣本單位數。在其他條件相同的情況下，樣本的單位數愈多，則抽樣誤差愈小。

　　3.抽樣方法。抽樣方法不同，抽樣誤差也不同。一般情況下重覆抽樣誤差比不重覆抽樣誤差要小一些。

　　4.抽樣調查的組織形式。不同的抽樣組織形式就有不同的抽樣誤差。

　　抽樣誤差則是不可避免的，但可以減少，其措施有：

　　1、增加樣本個案數。

　　2、適應選擇抽樣方式。

　　例如，在同樣條件下，又重覆抽樣比重覆抽樣的抽樣誤差小，又如在總體現象分類比較明顯時，採用分層隨機抽樣比其它方法的抽樣誤差小。由於總體真正的參數值未知，真正的抽樣誤差也未知，所以抽樣誤差的計算一般都以抽樣平均誤差來代表真正的抽樣誤差。