全球专业中文经管百科，由121,994位网友共同编写而成，共计435,826个条目

查看

工具▼

抽樣平均誤差

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

抽樣平均誤差（Sampling average error）

目錄

1 什麼是抽樣平均誤差
2 抽樣平均誤差的計算

什麼是抽樣平均誤差

　　抽樣平均誤差是抽樣平均數（或抽樣成數）的標準差，它反映抽樣平均數（或抽樣成數）與總體平均數（或總體成數）的平均差異程度。由於從一個總體可能抽取多個樣本，因此抽樣指標（如平均數、抽樣成數等），就有多個不同的數值，因而對全及指標（如總體平均數、總體成數等）的離差也就有大有小，這就必需用一個指標來衡量抽樣誤差的一般水平。

　　抽樣平均數的平均數等於總體平均數，抽樣成數的平均數等於總體總數，因而抽樣平均數（或抽樣成數）的標準差實際上反映了抽樣平均數（或抽樣成數）與總體平均數（或總體成數）的平均差異程度。

抽樣平均誤差的計算

　　（一）樣本平均數的平均誤差

　　以μx表示樣本平均數的平均誤差，表示總體的標準差。根據定義：

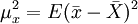
　　 $\mu_x^2=E(\bar{x}-\bar{X})^2$

　　1、當抽樣方式為重覆抽樣時，樣本標誌值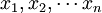 $x_1,x_2,\cdots x_n$ 是相互獨立的，樣本變數x與總體變數X同分佈。所以得：

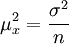　　 $\mu_x^2=\frac{\sigma^2}{n}$ 　　　　（1）

　　它說明在重覆抽樣的條件下，抽樣平均誤差與總體標準差成正比，與樣本容量的平方根成反比。

　　例1:有5個工人的日產量分別為（單位：件）：6，8，10，12，14，用重覆抽樣的方法，從中隨機抽取2個工人的日產量，用以代表這5個工人的總體水平。則抽樣平均誤差為多少？

　　解：根據題意可得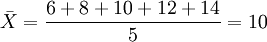： $\bar{X}=\frac{6+8+10+12+14}{5}=10$ (件)

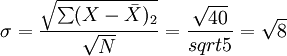　　總體標準差 $\sigma=\frac{\sqrt{\sum(X-\bar{X})_2}}{\sqrt{N}}=\frac{\sqrt{40}}{sqrt{5}}=\sqrt{8}$ (件)

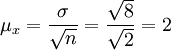　　抽樣平均誤差 $\mu_x=\frac{\sigma}{\sqrt{n}}=\frac{\sqrt{8}}{\sqrt{2}}=2$ (件)

　　2、當抽樣方式為不重覆抽樣時，樣本標誌值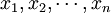 $x_1,x_2,\cdots,x_n$ 不是相互獨立的，根據數理統計知識可知：

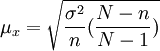　　 $\mu_x=\sqrt{\frac{\sigma^2}{n}(\frac{N-n}{N-1})}$ 　　　　（2）

　　當總體單位數N很大時，這個公式可近似表示為：

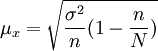　　 $\mu_x=\sqrt{\frac{\sigma^2}{n}(1-\frac{n}{N})}$ 　　　　（3）

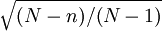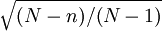　　與重覆抽樣相比，不重覆抽樣平均誤差是在重覆抽樣平均誤差的基礎上，再乘以 $\sqrt{(N-n)/(N-1)}$ ，而 $\sqrt{(N-n)/(N-1)}$ 總是小於1，所以不重覆抽樣的平均誤差也總是小於重覆抽樣的平均誤差。如前例，若改用不重覆抽樣方法，則抽樣平均誤差為：

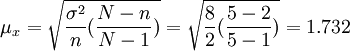　　 $\mu_x=\sqrt{\frac{\sigma^2}{n}(\frac{N-n}{N-1})}=\sqrt{\frac{8}{2}(\frac{5-2}{5-1})}=1.732$ (件)

　　在計算抽樣平均誤差時，通常得不到總體標準差的數值，一般可以用樣本標準差來代替總體標準差。

　　（二）抽樣成數的平均誤差

　　總體成數P可以表現為總體是非標誌的平均數。即E(X)＝P，它的標準差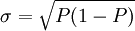 $\sigma=\sqrt{P(1-P)}$ 。

　　根據樣本平均誤差和總體標準差的關係，可以得到樣本成數的平均誤差的計算公式。

　　1、在重覆抽樣下

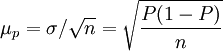　　 $\mu_p=\sigma/\sqrt{n}=\sqrt{\frac{P(1-P)}{n}}$ 　　　　（4）

　　2、在不重覆抽樣下

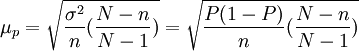　　 $\mu_p=\sqrt{\frac{\sigma^2}{n}(\frac{N-n}{N-1})}=\sqrt{\frac{P(1-P)}{n}(\frac{N-n}{N-1})}$ 　　　　（5）

　　當總體單位數N很大時，可近似地寫成：

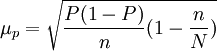　　 $\mu_p=\sqrt{\frac{P(1-P)}{n}(1-\frac{n}{N})}$ 　　　　（6）

　　當總體成數未知時，可以用樣本成數來代替。

　　例2：某企業生產的產品，按正常生產經驗，合格率為90%，現從5000件產品中抽取50件進行檢驗，求合格率的抽樣平均誤差。

　　解：根據題意，在重覆抽樣條件下，合格率的抽樣平均誤差為：

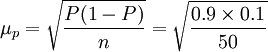
　　 $\mu_p=\sqrt{\frac{P(1-P)}{n}}=\sqrt{\frac{0.9\times 0.1}{50}}$

　　在不重覆抽樣條件下，合格率的抽樣平均誤差為：

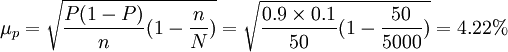
　　 $\mu_p=\sqrt{\frac{P(1-P)}{n}(1-\frac{n}{N})}=\sqrt{\frac{0.9\times 0.1}{50}(1-\frac{50}{5000})}=4.22%$

取自"https://wiki.mbalib.com/zh-tw/%E6%8A%BD%E6%A0%B7%E5%B9%B3%E5%9D%87%E8%AF%AF%E5%B7%AE"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

Zfj3000,Kane0135,Tears~,xq1202.

頁面分類: 統計術語

評論(共5條)

提示:評論內容為網友針對條目"抽樣平均誤差"展開的討論，與本站觀點立場無關。

123.150.183.* 在 2011年6月20日 22:35 發表

挺好

回複評論

111.193.231.* 在 2014年5月29日 10:31 發表

0.1哪來的

回複評論

Mis铭 (討論 | 貢獻) 在 2014年5月29日 15:51 發表

111.193.231.* 在 2014年5月29日 10:31 發表

0.1哪來的

依據算式(4)(5)代入計算而出，0.1為（1-P），P此時為例題中的合格率90%，即0.9，希望對您有幫助！

回複評論

183.94.32.* 在 2014年11月25日 22:32 發表

希望有推導過程

回複評論

111.18.49.* 在 2020年3月18日 14:07 發表

“抽樣平均數的平均數等於總體平均數，抽樣成數的平均數等於總體總數”這個結論對嗎？

回複評論

發表評論請文明上網，理性發言並遵守有關規定。

以上内容根据网友推荐自动排序生成

闽公网安备 35020302032707号