卡方分佈
出自 MBA智库百科(https://wiki.mbalib.com/)
卡方分佈(Chi-square Distribution)
目錄 |
卡方分佈 (χ2分佈)是概率論與統計學中常用的一種概率分佈。k 個獨立的標準正態分佈變數的平方和服從自由度為k 的卡方分佈。卡方分佈常用於假設檢驗和置信區間的計算。
若k 個隨機變數Z1、……、Zk 相互獨立,且數學期望為0、方差為 1(即服從標準正態分佈),則隨機變數X
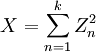
被稱為服從自由度為 k 的卡方分佈,記作
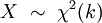
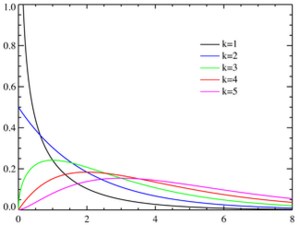
卡方分佈的概率密度函數為:
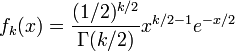
其中x≥0, 當x≤0時fk(x) = 0。這裡Γ代表Gamma 函數。
卡方分佈的累積分佈函數為:
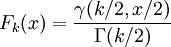
其中γ(k,z)為不完全Gamma函數
在大多數涉及卡方分佈的書中都會提供它的累積分佈函數的對照表。此外許多表格計算軟體如OpenOffice.org Calc和Microsoft Excel中都包括卡方分佈函數。
卡方分佈可以用來測試隨機變數之間是否相互獨立,也可用來檢測統計模型是否符合實際要求。
自由度為 k 的卡方變數的平均值是 k,方差是 2k。 卡方分佈是伽瑪分佈的一個特例,它的熵為:
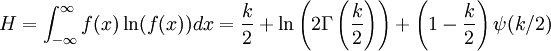
其中ψ(x) 是 Digamma function。
當Gamma變數頻率(λ)為1/2 時,α 的2倍為卡方變數之自由度(Degree of freedom)
即:
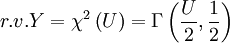
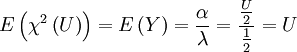
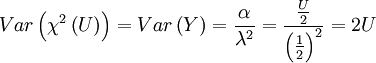
卡方變數之期望值=自由度卡方變數之方差=兩倍自由度
卡方分佈
| 參數 | k > 0, 自由度 |
| 值域 | 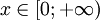 , ,
|
| 概率密度函數 | 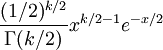 , ,
|
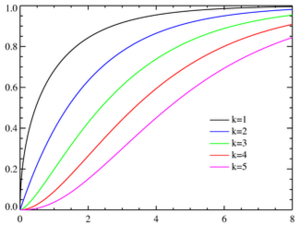
| 累積分佈函數(cdf) | 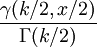 , ,
|
| 期望值 | k, |
| 中位數 | 大約k − 2 / 3, |
| 眾數 | k-2, if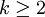 , ,
|
| 方差 | 2,k, |
| 偏態 | 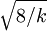 , ,
|
| 峰態 | 12/k, |
| 熵值 | 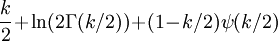
|
| 動差生成函數(mgf) | 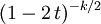 ,2t<1, ,2t<1,
|
| 特征函數 |  , ,
|
評論(共22條)
對於一些非學術類的詞條,評論的人很多,而對於這種真正核心學術的東西,竟然看不到多少人的評論,其實這沒太大意義。想學的自然上網去學,其餘的都是嘩眾取寵,都是烏合之眾,雖然寫著學到了多少東西,還評論說得對,其實根本都是口是心非,或許他們根本不知道這個詞條的真正含義。要真是個學術網站,沒必要做的像個科普網站一樣,這種網站應該是定向的,對專業人士的,而不是對大眾開放,毫無意義,比如這個卡方分佈,有幾個閑人明白?學術百科可不是百科全書,學術就是學術好吧?
看不懂你要說什麼……可不可以補充一個正態分佈推導卡方分佈的證明啊
看不懂你要說什麼……可不可以補充一個正態分佈推導卡方分佈的證明啊
高級統計學里都有的,關於正態分佈推導卡方分佈的過程、t分佈、f分佈等等。
對於一些非學術類的詞條,評論的人很多,而對於這種真正核心學術的東西,竟然看不到多少人的評論,其實這沒太大意義。想學的自然上網去學,其餘的都是嘩眾取寵,都是烏合之眾,雖然寫著學到了多少東西,還評論說得對,其實根本都是口是心非,或許他們根本不知道這個詞條的真正含義。要真是個學術網站,沒必要做的像個科普網站一樣,這種網站應該是定向的,對專業人士的,而不是對大眾開放,毫無意義,比如這個卡方分佈,有幾個閑人明白?學術百科可不是百科全書,學術就是學術好吧?
以上的邏輯和斷句,不僅“學術”,而且“專業”,真是讓人心服口服。
您能推薦幾本高級統計學的書籍嗎?
對於一些非學術類的詞條,評論的人很多,而對於這種真正核心學術的東西,竟然看不到多少人的評論,其實這沒太大意義。想學的自然上網去學,其餘的都是嘩眾取寵,都是烏合之眾,雖然寫著學到了多少東西,還評論說得對,其實根本都是口是心非,或許他們根本不知道這個詞條的真正含義。要真是個學術網站,沒必要做的像個科普網站一樣,這種網站應該是定向的,對專業人士的,而不是對大眾開放,毫無意義,比如這個卡方分佈,有幾個閑人明白?學術百科可不是百科全書,學術就是學術好吧?
學術的最終目的是什麼? 開口閉口學術透著一股濃濃的優越感,真是嚇死寶寶了。 專業人士,不對大眾開放,瞧瞧這自詡精英階級的嘴臉。 嚇得我還以為先生您生下來就戴著眼鏡開始學術研究了呢。
對於一些非學術類的詞條,評論的人很多,而對於這種真正核心學術的東西,竟然看不到多少人的評論,其實這沒太大意義。想學的自然上網去學,其餘的都是嘩眾取寵,都是烏合之眾,雖然寫著學到了多少東西,還評論說得對,其實根本都是口是心非,或許他們根本不知道這個詞條的真正含義。要真是個學術網站,沒必要做的像個科普網站一樣,這種網站應該是定向的,對專業人士的,而不是對大眾開放,毫無意義,比如這個卡方分佈,有幾個閑人明白?學術百科可不是百科全書,學術就是學術好吧?
大學普通課程,謝謝。
可否推薦一本高級統計學的書?謝謝
對於一些非學術類的詞條,評論的人很多,而對於這種真正核心學術的東西,竟然看不到多少人的評論,其實這沒太大意義。想學的自然上網去學,其餘的都是嘩眾取寵,都是烏合之眾,雖然寫著學到了多少東西,還評論說得對,其實根本都是口是心非,或許他們根本不知道這個詞條的真正含義。要真是個學術網站,沒必要做的像個科普網站一樣,這種網站應該是定向的,對專業人士的,而不是對大眾開放,毫無意義,比如這個卡方分佈,有幾個閑人明白?學術百科可不是百科全書,學術就是學術好吧?
什麼算閑人啊 看來你是真閑才寫這麼一大段和卡方分佈一點關係都沒的評論 你問問現在的大學生誰不知道卡方分佈啊
對於一些非學術類的詞條,評論的人很多,而對於這種真正核心學術的東西,竟然看不到多少人的評論,其實這沒太大意義。想學的自然上網去學,其餘的都是嘩眾取寵,都是烏合之眾,雖然寫著學到了多少東西,還評論說得對,其實根本都是口是心非,或許他們根本不知道這個詞條的真正含義。要真是個學術網站,沒必要做的像個科普網站一樣,這種網站應該是定向的,對專業人士的,而不是對大眾開放,毫無意義,比如這個卡方分佈,有幾個閑人明白?學術百科可不是百科全書,學術就是學術好吧?
也許,大一,數理統計必修
這不是統計學基礎嗎。。
概率統計那本書里的卡方分佈只是卡方分佈的一個特殊情況,即上面所說的,一般大學生也就知道這個特殊的,除非學過高級統計吧,我看的心理統計中的概念就比這個廣泛多了,如果想瞭解一下,可以簡單的看張厚粲的《現代心理與教育統計學》第四版P187-189
對於一些非學術類的詞條,評論的人很多,而對於這種真正核心學術的東西,竟然看不到多少人的評論,其實這沒太大意義。想學的自然上網去學,其餘的都是嘩眾取寵,都是烏合之眾,雖然寫著學到了多少東西,還評論說得對,其實根本都是口是心非,或許他們根本不知道這個詞條的真正含義。要真是個學術網站,沒必要做的像個科普網站一樣,這種網站應該是定向的,對專業人士的,而不是對大眾開放,毫無意義,比如這個卡方分佈,有幾個閑人明白?學術百科可不是百科全書,學術就是學術好吧?
有理,本人學生,總想快速找到精準的瑣碎知識,希望有權威的學術問答
對於一些非學術類的詞條,評論的人很多,而對於這種真正核心學術的東西,竟然看不到多少人的評論,其實這沒太大意義。想學的自然上網去學,其餘的都是嘩眾取寵,都是烏合之眾,雖然寫著學到了多少東西,還評論說得對,其實根本都是口是心非,或許他們根本不知道這個詞條的真正含義。要真是個學術網站,沒必要做的像個科普網站一樣,這種網站應該是定向的,對專業人士的,而不是對大眾開放,毫無意義,比如這個卡方分佈,有幾個閑人明白?學術百科可不是百科全書,學術就是學術好吧?
有理,本人學生,總想快速找到精準的瑣碎知識,希望有權威的學術問答
對於一些非學術類的詞條,評論的人很多,而對於這種真正核心學術的東西,竟然看不到多少人的評論,其實這沒太大意義。想學的自然上網去學,其餘的都是嘩眾取寵,都是烏合之眾,雖然寫著學到了多少東西,還評論說得對,其實根本都是口是心非,或許他們根本不知道這個詞條的真正含義。要真是個學術網站,沒必要做的像個科普網站一樣,這種網站應該是定向的,對專業人士的,而不是對大眾開放,毫無意義,比如這個卡方分佈,有幾個閑人明白?學術百科可不是百科全書,學術就是學術好吧?
這不是基礎課程?








對於一些非學術類的詞條,評論的人很多,而對於這種真正核心學術的東西,竟然看不到多少人的評論,其實這沒太大意義。想學的自然上網去學,其餘的都是嘩眾取寵,都是烏合之眾,雖然寫著學到了多少東西,還評論說得對,其實根本都是口是心非,或許他們根本不知道這個詞條的真正含義。要真是個學術網站,沒必要做的像個科普網站一樣,這種網站應該是定向的,對專業人士的,而不是對大眾開放,毫無意義,比如這個卡方分佈,有幾個閑人明白?學術百科可不是百科全書,學術就是學術好吧?