卡方分布
出自 MBA智库百科(https://wiki.mbalib.com/)
卡方分布(Chi-square Distribution)
目录 |
卡方分布 (χ2分布)是概率论与统计学中常用的一种概率分布。k 个独立的标准正态分布变量的平方和服从自由度为k 的卡方分布。卡方分布常用于假设检验和置信区间的计算。
若k 个随机变量Z1、……、Zk 相互独立,且数学期望为0、方差为 1(即服从标准正态分布),则随机变量X
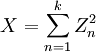
被称为服从自由度为 k 的卡方分布,记作
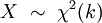
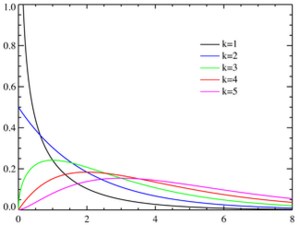
卡方分布的概率密度函数为:
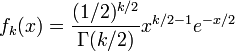
其中x≥0, 当x≤0时fk(x) = 0。这里Γ代表Gamma 函数。
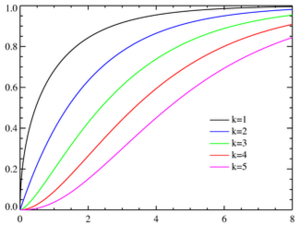
卡方分布的累积分布函数为:
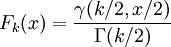
其中γ(k,z)为不完全Gamma函数
在大多数涉及卡方分布的书中都会提供它的累积分布函数的对照表。此外许多表格计算软件如OpenOffice.org Calc和Microsoft Excel中都包括卡方分布函数。
卡方分布可以用来测试随机变量之间是否相互独立,也可用来检测统计模型是否符合实际要求。
自由度为 k 的卡方变量的平均值是 k,方差是 2k。 卡方分布是伽玛分布的一个特例,它的熵为:
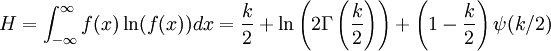
其中ψ(x) 是 Digamma function。
当Gamma变数频率(λ)为1/2 时,α 的2倍为卡方变数之自由度(Degree of freedom)
即:
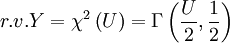
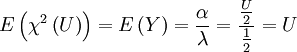
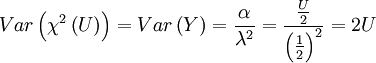
卡方变数之期望值=自由度卡方变数之方差=两倍自由度
卡方分布
| 参数 | k > 0, 自由度 |
| 值域 | 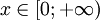 , ,
|
| 概率密度函数 | 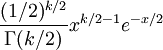 , ,
|
| 累积分布函数(cdf) | 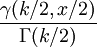 , ,
|
| 期望值 | k, |
| 中位数 | 大约k − 2 / 3, |
| 众数 | k-2, if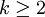 , ,
|
| 方差 | 2,k, |
| 偏态 | 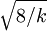 , ,
|
| 峰态 | 12/k, |
| 熵值 | 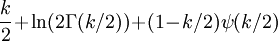
|
| 动差生成函数(mgf) | 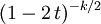 ,2t<1, ,2t<1,
|
| 特征函数 |  , ,
|
评论(共22条)
对于一些非学术类的词条,评论的人很多,而对于这种真正核心学术的东西,竟然看不到多少人的评论,其实这没太大意义。想学的自然上网去学,其余的都是哗众取宠,都是乌合之众,虽然写着学到了多少东西,还评论说得对,其实根本都是口是心非,或许他们根本不知道这个词条的真正含义。要真是个学术网站,没必要做的像个科普网站一样,这种网站应该是定向的,对专业人士的,而不是对大众开放,毫无意义,比如这个卡方分布,有几个闲人明白?学术百科可不是百科全书,学术就是学术好吧?
看不懂你要说什么……可不可以补充一个正态分布推导卡方分布的证明啊
看不懂你要说什么……可不可以补充一个正态分布推导卡方分布的证明啊
高级统计学里都有的,关于正态分布推导卡方分布的过程、t分布、f分布等等。
对于一些非学术类的词条,评论的人很多,而对于这种真正核心学术的东西,竟然看不到多少人的评论,其实这没太大意义。想学的自然上网去学,其余的都是哗众取宠,都是乌合之众,虽然写着学到了多少东西,还评论说得对,其实根本都是口是心非,或许他们根本不知道这个词条的真正含义。要真是个学术网站,没必要做的像个科普网站一样,这种网站应该是定向的,对专业人士的,而不是对大众开放,毫无意义,比如这个卡方分布,有几个闲人明白?学术百科可不是百科全书,学术就是学术好吧?
以上的逻辑和断句,不仅“学术”,而且“专业”,真是让人心服口服。
您能推荐几本高级统计学的书籍吗?
对于一些非学术类的词条,评论的人很多,而对于这种真正核心学术的东西,竟然看不到多少人的评论,其实这没太大意义。想学的自然上网去学,其余的都是哗众取宠,都是乌合之众,虽然写着学到了多少东西,还评论说得对,其实根本都是口是心非,或许他们根本不知道这个词条的真正含义。要真是个学术网站,没必要做的像个科普网站一样,这种网站应该是定向的,对专业人士的,而不是对大众开放,毫无意义,比如这个卡方分布,有几个闲人明白?学术百科可不是百科全书,学术就是学术好吧?
学术的最终目的是什么? 开口闭口学术透着一股浓浓的优越感,真是吓死宝宝了。 专业人士,不对大众开放,瞧瞧这自诩精英阶级的嘴脸。 吓得我还以为先生您生下来就戴着眼镜开始学术研究了呢。
对于一些非学术类的词条,评论的人很多,而对于这种真正核心学术的东西,竟然看不到多少人的评论,其实这没太大意义。想学的自然上网去学,其余的都是哗众取宠,都是乌合之众,虽然写着学到了多少东西,还评论说得对,其实根本都是口是心非,或许他们根本不知道这个词条的真正含义。要真是个学术网站,没必要做的像个科普网站一样,这种网站应该是定向的,对专业人士的,而不是对大众开放,毫无意义,比如这个卡方分布,有几个闲人明白?学术百科可不是百科全书,学术就是学术好吧?
大学普通课程,谢谢。
可否推荐一本高级统计学的书?谢谢
对于一些非学术类的词条,评论的人很多,而对于这种真正核心学术的东西,竟然看不到多少人的评论,其实这没太大意义。想学的自然上网去学,其余的都是哗众取宠,都是乌合之众,虽然写着学到了多少东西,还评论说得对,其实根本都是口是心非,或许他们根本不知道这个词条的真正含义。要真是个学术网站,没必要做的像个科普网站一样,这种网站应该是定向的,对专业人士的,而不是对大众开放,毫无意义,比如这个卡方分布,有几个闲人明白?学术百科可不是百科全书,学术就是学术好吧?
什么算闲人啊 看来你是真闲才写这么一大段和卡方分布一点关系都没的评论 你问问现在的大学生谁不知道卡方分布啊
对于一些非学术类的词条,评论的人很多,而对于这种真正核心学术的东西,竟然看不到多少人的评论,其实这没太大意义。想学的自然上网去学,其余的都是哗众取宠,都是乌合之众,虽然写着学到了多少东西,还评论说得对,其实根本都是口是心非,或许他们根本不知道这个词条的真正含义。要真是个学术网站,没必要做的像个科普网站一样,这种网站应该是定向的,对专业人士的,而不是对大众开放,毫无意义,比如这个卡方分布,有几个闲人明白?学术百科可不是百科全书,学术就是学术好吧?
也许,大一,数理统计必修
这不是统计学基础吗。。
概率统计那本书里的卡方分布只是卡方分布的一个特殊情况,即上面所说的,一般大学生也就知道这个特殊的,除非学过高级统计吧,我看的心理统计中的概念就比这个广泛多了,如果想了解一下,可以简单的看张厚粲的《现代心理与教育统计学》第四版P187-189
对于一些非学术类的词条,评论的人很多,而对于这种真正核心学术的东西,竟然看不到多少人的评论,其实这没太大意义。想学的自然上网去学,其余的都是哗众取宠,都是乌合之众,虽然写着学到了多少东西,还评论说得对,其实根本都是口是心非,或许他们根本不知道这个词条的真正含义。要真是个学术网站,没必要做的像个科普网站一样,这种网站应该是定向的,对专业人士的,而不是对大众开放,毫无意义,比如这个卡方分布,有几个闲人明白?学术百科可不是百科全书,学术就是学术好吧?
有理,本人学生,总想快速找到精准的琐碎知识,希望有权威的学术问答
对于一些非学术类的词条,评论的人很多,而对于这种真正核心学术的东西,竟然看不到多少人的评论,其实这没太大意义。想学的自然上网去学,其余的都是哗众取宠,都是乌合之众,虽然写着学到了多少东西,还评论说得对,其实根本都是口是心非,或许他们根本不知道这个词条的真正含义。要真是个学术网站,没必要做的像个科普网站一样,这种网站应该是定向的,对专业人士的,而不是对大众开放,毫无意义,比如这个卡方分布,有几个闲人明白?学术百科可不是百科全书,学术就是学术好吧?
有理,本人学生,总想快速找到精准的琐碎知识,希望有权威的学术问答
对于一些非学术类的词条,评论的人很多,而对于这种真正核心学术的东西,竟然看不到多少人的评论,其实这没太大意义。想学的自然上网去学,其余的都是哗众取宠,都是乌合之众,虽然写着学到了多少东西,还评论说得对,其实根本都是口是心非,或许他们根本不知道这个词条的真正含义。要真是个学术网站,没必要做的像个科普网站一样,这种网站应该是定向的,对专业人士的,而不是对大众开放,毫无意义,比如这个卡方分布,有几个闲人明白?学术百科可不是百科全书,学术就是学术好吧?
这不是基础课程?








对于一些非学术类的词条,评论的人很多,而对于这种真正核心学术的东西,竟然看不到多少人的评论,其实这没太大意义。想学的自然上网去学,其余的都是哗众取宠,都是乌合之众,虽然写着学到了多少东西,还评论说得对,其实根本都是口是心非,或许他们根本不知道这个词条的真正含义。要真是个学术网站,没必要做的像个科普网站一样,这种网站应该是定向的,对专业人士的,而不是对大众开放,毫无意义,比如这个卡方分布,有几个闲人明白?学术百科可不是百科全书,学术就是学术好吧?