整群抽樣
出自 MBA智库百科(https://wiki.mbalib.com/)
整群抽樣 (Cluster sampling)
目錄 |
整群抽樣又稱聚類抽樣。是將總體中各單位歸併成若幹個互不交叉、互不重覆的集合,稱之為群;然後以群為抽樣單位抽取樣本的一種抽樣方式。
應用整群抽樣時,要求各群有較好的代表性,即群內各單位的差異要大,群間差異要小。
整群抽樣的優點是實施方便、節省經費;
整群抽樣的缺點是往往由於不同群之間的差異較大,由此而引起的抽樣誤差往往大於簡單隨機抽樣。
| 市場調查方法 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [編輯] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
先將總體分為i個群,然後從i個群中隨機抽取若幹個群,對這些群內所有的或部分選中的個體或單元均進行調查。抽樣過程可分為以下幾個步驟:
一、確定分群的標準。
二、總體(N)分成若幹個互不重疊的部分,每個部分為一群。
三、據各樣本量,確定應該抽取的群數。
四、採用簡單隨機抽樣或系統抽樣方法,從i群中抽取確定數量的個體或單元。
整群抽樣的誤差[1]
整群抽樣的誤差視各群單位方差大小而定,各群單位方差的簡單平均數是計算其抽樣平均誤差的依據。從公式上看,整群抽樣平均誤差的公式與類型抽樣平均誤差的公式相似,用R表示全及總體中劃分的群(組)數。r表示被抽中的群(組)數。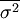 表示抽樣總體各群(組)方差的平均數。
表示抽樣總體各群(組)方差的平均數。
整群抽樣平均數的抽樣平均誤差為:
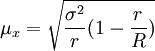
成數的抽樣平均誤差為:
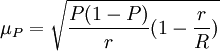
整群抽樣與分層抽樣在形式上有相似之處,但實際上差別很大。
分層抽樣要求各層之間的差異很大,層內個體或單元差異小,而整群抽樣要求群與群之間的差異比較小,群內個體或單元差異大;
分層抽樣的樣本時從每個層內抽取若幹單元或個體構成,而整群抽樣則是要麼整群抽取,要麼整群不被抽取。
分層抽樣與整群抽樣對比
1.分層抽樣
某公司的雇員按照部門(銷售部、市場部、研究部、廣告部)分層,在每一個部門隨機抽取10名雇員。
2.整群抽樣
福爾摩斯特旅館連鎖店有10家酒店,從中隨機地選取5家,對被選出的每家酒店的全部雇員進行調查。
案例一:整群抽樣在平原綠化調查中的應用[2]
平原綠化調查一般是指針對一個縣或幾個縣的較大範圍內進行調查,調查內容比較多,範圍廣,困難大。以往採用的公裡網機械布點調查方法,在調查時,布點工作量大,時間長,操作很不方便。近幾年在村鎮綠化率及農田林網化調查時,我們採用了整群抽樣法進行調查,取得了很好的效果,大大減輕了布點工作量,並且其調查統計中的各個特征數完全能夠達到預定的要求。我們認為,這種抽樣方法可以在平原綠化調查或其他較大範圍的林業調查中推廣應用。
一、整群抽樣技術簡介
整群抽樣是將全部總體單元劃分為若幹部分,把劃分的每一部分稱為一個“群”,然後抽取若幹個“群”,對這些“群”進行調查,估計總體。
在將全部總體單元劃分為若幹群時,有下列要求:第一,群與群之間無重疊,即任何一個總體單元只屬於某一個群;第二,全部總體單元毫無遺漏,即任何一個總體單元必定屬於某一個群;第三,每一個群包含的單元數可以是相同的,也可以是不相同的,但必須是確知的。
在對群進行抽樣,以組成樣本時,可以採取等概方式,也可以採取不等概方式;可以採取重覆抽樣方式,也可以採取不重覆抽樣方式。
用整群抽樣法對總體進行估計時,根據每個群內包含的總體單元數是否相等,分等群估計和不等群估計兩種方法。
二、整群抽樣法的應用
在陵縣、臨邑兩縣村莊綠化率調查的方法介紹如下:
1.劃分群體、抽樣
兩縣村莊占地面積共2.6萬h㎡ ,將667㎡土地作為一個總體單元,即有39萬個總體單元,這些總體單元分佈在2165個村中。根據總體劃分群的要求,我們可以將村做為群,則兩個縣共有2165個群。每群所包括的單元數為各村的占地面積數。
由於每個村面積不等,即每個群的單元數是不相等的,所以我們劃分的群是不等群,在進行總體估計時,用不等群估計方法。
抽取樣本的個數,應根據總體的變動繫數來確定。這裡,我們預計變動繫數時,用下麵方法進行計算:根據檔案材料,查找出兩個縣前一年的統計報表,在報表中隨機抽出50 個村的林木覆蓋數字,以此做為樣本,求出其標準差和平均數,由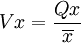 求得變動繫數為0.41 ,這個數字可做為總體的估計變動繫數。
求得變動繫數為0.41 ,這個數字可做為總體的估計變動繫數。
根據估計的變動繫數及95 %的可靠性(ua=1.96) 和90%的精度(P) 要求, 由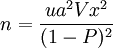 求得樣本個數為:
求得樣本個數為: 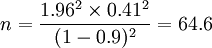 取整數為65 。
取整數為65 。
在總體所有的群中,用簡單隨機抽樣法等概地抽取65 個群組成樣本,對總體進行估計。
2.樣群調查
對抽中的村莊四旁樹木進行逐棵查數,每隔10株測算一棵樹冠投影面積,以算術平均法求得每株平均投影面積,再乘以總株數得林木覆蓋面積。
通過全面調查,獲得65個樣群的調查資料,調查數據按樣群編號1 ,2 ,3 ……65列出, ( 省略村名) 。見下表
表 65個樣群調查數據
| 樣群號i | 林木覆蓋面積yi | 樣群號i | 林木覆蓋面積yi | 樣群號i | 林木覆蓋面積yi |
| 1 | 96 | 23 | 95 | 45 | 43 |
| 2 | 49 | 24 | 72 | 46 | 114 |
| 3 | 71 | 25 | 43 | 47 | 92 |
| 4 | 29 | 26 | 88 | 48 | 95 |
| 5 | 58 | 27 | 36 | 49 | 109 |
| 6 | 31 | 28 | 36 | 50 | 121 |
| 7 | 82 | 29 | 74 | 51 | 130 |
| 8 | 44 | 30 | 52 | 52 | 72 |
| 9 | 88 | 31 | 63 | 53 | 90 |
| 10 | 65 | 32 | 44 | 54 | 57 |
| 11 | 56 | 33 | 60 | 55 | 37 |
| 12 | 38 | 34 | 35 | 56 | 33 |
| 13 | 78 | 35 | 62 | 57 | 40 |
| 14 | 85 | 36 | 40 | 58 | 53 |
| 15 | 58 | 37 | 67 | 59 | 26 |
| 16 | 83 | 38 | 43 | 60 | 50 |
| 17 | 40 | 39 | 72 | 61 | 59 |
| 18 | 60 | 40 | 82 | 62 | 72 |
| 19 | 62 | 41 | 67 | 63 | 57 |
| 20 | 52 | 42 | 74 | 64 | 54 |
| 21 | 39 | 43 | 27 | 65 | 53 |
| 22 | 77 | 44 | 49 | Σyi | 4037 |
3.計算
因為調查的村莊林木覆蓋率為頻率範圍,因而採用總體頻率的不等群估計方法。
村莊林木覆蓋率(總體頻率) 整群抽樣估計值為:
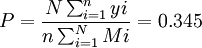 即34.5%
即34.5%
估計誤差限為:
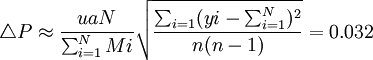
總體頻率P的置信區為[P-ΔP,P+ΔP]即[31.3%,37.7%]。如果計算精度,則估計精度為1-ΔP/P=90.7%。式中:P為總體頻率,N為總體內全部群數,n為樣本群數,yi為具備某特征單元數,Mi為每群單元數。
三、使用整群抽樣應註意的幾個問題
1.只有在總體單元數非常大,群數相當多時,才能用整群抽樣進行估計取得整群抽樣的估計效率。
2.只有總體中N 群的Yi具有正態(近似正態) 的頻率分佈時,才可採用小樣本估計方法。
3.劃分的各群內單元數相同的,採用整群抽樣的等群估計方法,其主要公式為:
(1) 總體平均數估計值:樣群誤差限:
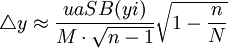
其中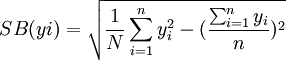
(2) 總體頻率的估計值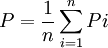
估計誤差限: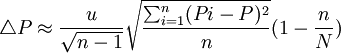
式中:y 為樣本平均數: P為樣本頻率;yi、Pi為樣本標誌值; n為樣本個數;M為一個群所含的單元數;SB(yi) 為標準差。








如果有案例就好了!