統計質量控制
出自 MBA智库百科(https://wiki.mbalib.com/)
統計質量控制(SQC-Statistical Quality Control)
目錄 |
20世紀30年代Walter Shewart的統計質量控制原理,已有60多年曆史。W. Edwards Deming和Joseph Juran 在20世紀40和50年代發展了這些原理,併在實踐中得到了證明,特別是在日本,獲得了極大的成功。
質量控制的數理統計學基礎
1.計量值數據
(長度、重量、電流、溫度等。測量結果的數據可以是連續的,也可以是不連續的)
2.計數值數據
不能連續取值的,只能以個數計算的數為計數值數據。(不合格品數、缺陷數)
把所研究的對象的全體稱為全及總體,也叫做母體或簡稱為總體。
通常全及總體的單位數用N來表示,樣本單位數稱為樣本容量,用n來表示。相對於N來說,n則是個很小的數。它可以是總體的幾十分之一乃至幾萬分之一。
數據特征值是數據分佈趨勢的一種度量。數據特征值可以分為兩類。
1.表示數據集中趨勢的特征值
(1)頻數
計算各個值反覆出現的次數,稱之為頻數。
(2)算術平均值
如果產品質量有n個測量數據xi(i=1,2,…,n),平均值為:
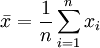
如果測量數據按大小分組,則平均值為
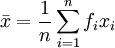
(3)中位數
數據按大小順序排列,排在中間的那個數稱為中位數。用表示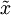 。當數據總數為奇數時,最中間的數就是;當數據總數為偶數時,中位數為中間兩個數據的平均值。
。當數據總數為奇數時,最中間的數就是;當數據總數為偶數時,中位數為中間兩個數據的平均值。
(4)眾數
眾數是一組測量數據中出現次數(頻數)最多的那個數值,一般用M0表示。
2.表示數據離散程度的特征值
(1) 極差
極差是一組測量數據中的最大值和最小值之差。通常用於表示不分組數據的離散度,用符號R表示。
R = xmax − xmin
(2) 平均偏差
將每個數據減去平均值,並把它們的差值的絕對值相加再除以測量數據的總個數,即得到平均偏差,用AD表示。
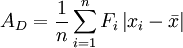
(3)均方根偏差
均方根偏差是測量數據平均值之差的平方和被總測數平均,然後再求其平均值,用σ表示。
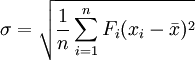
用均方根偏差作為的度量,可以直接比較兩組數據的均方根偏差的大小就可看出兩組數據離散程度的大小。
(4)標準偏差
測量數據分佈的離散最重要的度量是標準偏差,用S表示。對於大量生產的產品來說,不可能對全部產品進行檢驗,通常只對其中一部分產品(樣本)進行檢驗。當把有限數量產品測量數據按標準方差的公式求得的樣本方差和總體方差作一比較,會發現這個估計值將偏小。因此,必須用因數n/n-1乘上樣本方差來修正,則樣本標準方差S2為:
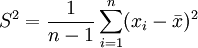
把樣本標準方差開平方後,可得樣本標準偏差為
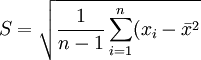
當計算樣本標準偏差時,隨著樣本大小n增大,便愈接近,則標準偏差估計值得誤差將會縮小。
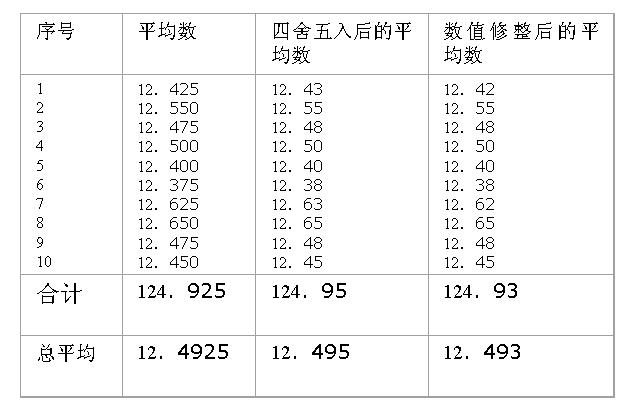
數據的修整
過多的四捨五入會造成誤差過大,可採取進位和捨棄機會均等的修整方法:
1)位數>5,則:進位並捨去後面的數。
2)位數< 5 ,則:捨去,及後面的數。
3)位數=5,則:
a) 後面的數為0或無數字,5前面的數為奇數進一、偶數捨去。
b) 後面的數不全為零, 5前面的數進一、捨去5和以後的數。
4)不得連續進行修整。
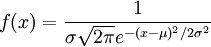
式中,μ為總體的算術平均值;σ為總體的標準偏差;
如果我們令Z=(x-μ)/σ,那麼我們可以得到正態密度函數標準化形式為

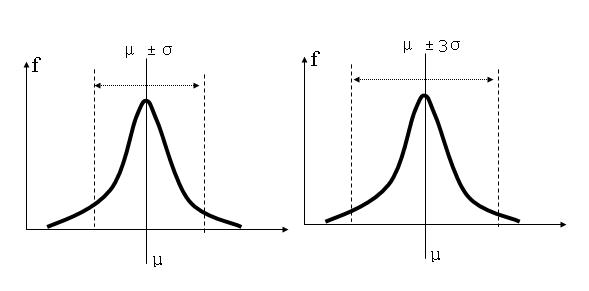
面積是全體變數的68.26%落在μ±σ的範圍之內;
95.46%的變數是落在μ±2σ界限之內;
99.73%的變數落在μ±3σ界限之內。
但是,必須特別註意,在同樣的兩個已知界限內,對於樣本界限內所占的百分比同總體界線內所占的百分比可能不很一致。這個差別非常重要,它構成了假設檢驗的基本原理。
調查表是為了調查客觀事物、產品和工作質量,或為了分層收集數據而設計的圖表。即把產品可能出現的情況及其分類預先列成調查表,則檢查產品時只需在相應分類中進行統計。
為了能夠獲得良好的效果、可比性、全面性和準確性,調查表格設計應簡單明瞭,突出重點;應填寫方便,符號好記;調查、加工和檢查的程式與調查表填寫次序應基本一致,填寫好的調查表要定時、準時更換並保存,數據要便於加工整理,分析整理後及時反饋。
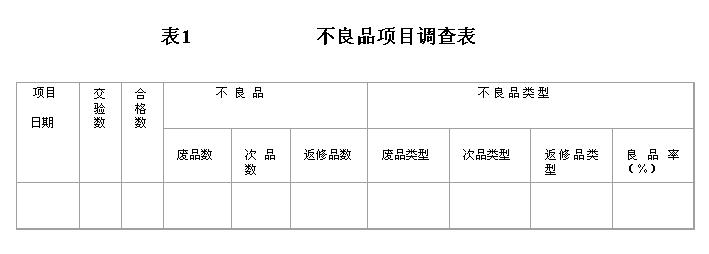
1.不良項目調查表
質量管理中“良”與“不良”,是相對於標準、規格、公差而言的。一個零件和產品不符合標準、規格、公差的質量項目叫不良項目,也稱不合格項目。
如表1
2.缺陷位置調查表
缺陷位置調查表宜與措施相聯繫,能充分反映缺陷發生的位置,便於研究缺陷為什麼集中在那裡,有助於進一步觀察、探討發生的原因。缺陷位置調查表可根據具體情況畫出各種不同的缺陷位置調查表,圖上可以劃區,以便進行分層研究和對比分析。
3.頻數調查表
為了做直方圖而需經過收集數據、分組、統計頻數、計算、繪圖等步驟。如果運用頻數調查表,那就在收集數據的同時,直接進行分解和統計頻數。
4.檢查確認調查表
檢查確認調查表是對所做工作和加工的質量進行總的檢查與確認。在有限的時間內檢查太多的項目,稍有疏忽,同一項目可能檢查兩次,而有的項目可能漏檢。因此,當檢查項目較多時(100項以上),為了不致弄錯或遺漏,預先把應檢查的項目統統列出來,然後按順序,每檢查一項在相應處作記號,防止遺漏。
5.作業抽樣調查表
作業抽樣是分析作業時間的方法。它將全部時間分為加工、準備、空閑的時間,然後通過任意時刻,反覆多次瞬間觀測作業的內容,進而調查各段時間占全部時間的百分比。
目前,調查表廣泛應用於各行各業,調查表的形式也多種多樣。
分層就是把所收集的數據進行合理的分類,把性質相同、在同一生產條件下收集的數據歸在一起,把劃分的組叫做“層”,通過數據分層把錯綜複雜的影響質量因素分析清楚。
當分層分不好時,會使圖形的規律性隱蔽起來,還會造成假象。例如:
- 作直方圖分層不好時,就會出現雙峰型和平頂型。
- 排列圖分層不好時,無法區分主要因素和次要因素,也無法對主要因素作進一步分析。
- 散佈圖分層不好時,會出現幾簇互不關連的散點群。
- 控製圖分層不好時,無法反映工序的真實變化,不能找出數據異常的原因,不能作出正確的判斷。
- 因果圖分層不好時,不能搞清大原因、中原因、小原因之間的真實傳遞途徑。
例1:
在柴油機裝配中經常發生氣缸墊漏氣現象,為解決這一質量問題,對該工序進行現場統計。
(1)收集數據:n=50,漏氣數f=19,漏氣率 p =38%
(2)分析原因
通過分析,漏氣可能有兩個原因:
a)該工序塗密封劑的工人A、B、C三人的操作方法有差異;
b)氣缸墊分別由甲、乙兩廠供給,原材料有差異。
因此,作分層表
由分層表,人們似乎以為,降低氣缸漏氣率的辦法可採用乙廠提供的氣缸墊和工人B的操作方法。
但實踐結果表明,這樣做漏氣率非但沒有降低,反而增加到43%,這是什麼原因呢
為此,進行更細緻的綜合分析。
經綜合分析後再次提出降低氣缸漏氣率的措施是:使用甲廠提供的氣缸墊時,要採用工人B的操作方法。
使用乙廠提供的氣缸墊時,要採用工人A的操作方法。
實踐表明,上述的分層法及採用的措施十分有效,漏氣率大大降低。
直方圖法是適用於對大量計量值數據進行整理加工,找出其統計規律,即分析數據分佈的形態,以便對其總體的分佈特征進行推斷,對工序或批量產品的質量水平及其均勻程度進行分析的方法。
1.作直方圖的方法步驟如下
(1) 收集數據
一般收集數據都要隨機抽取50個以上質量特性數據,最好是100個以上的數據,並按先後順序排列。 (2) 找出數據中的最大值,最小值和極差。
數據中的最大值用xmax表示,最小值用xmin表示,極差用R表示。
例2
某項目統計數據為:
xmax=63,xmin=38,
極差R=xmax − xmin=63-38=25。
區間[xmax,xmin]稱為數據的散佈範圍
(3)確定組數。
組數常用符號k表示。k與數據數多少有關。數據多,多分組;數據少,少分組。
例2中100個數據,常分為10組左右。
也有人用這樣一個經驗公式計算組數:k=1+3.31(logn)
例2中n=100,故:
k=1+3.31(1ogn)=1+3.31(log100)=7.62≈8
一般由於正態分佈為對稱形,故常取k為奇數。
所以例2中取k=9。
(4)求出組距(h)。
組距即組與組之間的間隔,等於極差除以組數,即
組距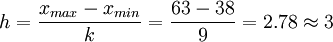
(5)確定組界
為了確定邊界,通常從最小值開始。先把最小值放在第一組的中間位置上。
例2中數據最小值xmin=38,組距(h)=3,故第一組的組界為:
(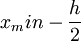 )~(
)~(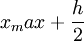 )
)
(6)計算各組的組中值(wi)。
- 所謂組中值,就是處於各組中心位置的數值,又叫中心值。
- 某組的中心值(wi)=(某組的上限+某組的下限)/2
- 第一組的中心值(w1)=(36.5+39.5)/ 2=38
- 第二組的中心值(w2)=(39.5+42.5 2)/2=41
- 其它各組類推。
(7)統計各組頻數。
統計頻數的方法。
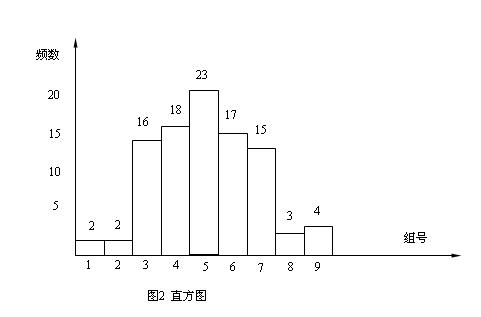
(8)畫直方圖。
以分組號為橫坐標,以頻數為高度作縱坐標,作成直方圖,如圖2所示。
2.直方圖的用途
直方圖在生產中是經常使用的簡便且能發揮很大作用的統計方法。其主要作用是:
(1)觀察與判斷產品質量特性分佈狀態
(2)判斷工序是否穩定。
(3)計算工序能力,估算並瞭解工序能力對產品質量保證情況。
3.直方圖的觀察與分析
對直方圖的觀察,主要有兩個方面:一是分析直方圖的全圖形狀,能夠發現生產過程的一些質量問題;二是把直方圖和質量指標比較,觀察質量是否滿足要求。
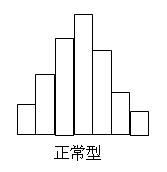
直方圖可分為正常型和非正常型,下麵分別它們的形狀。
(1)正常型
圖形中央有一頂峰,左右大致對稱,這時工序處於穩定狀態。其它都屬非正常型。
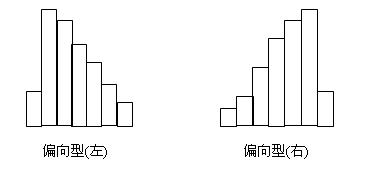
(2) 偏向型
圖形有偏左、偏右兩種情形,原因是:
(a)一些形位公差要求的特性值是偏向分佈。
(b)加工者擔心出現不合格品,在加工孔時往往偏小,加工軸時往往偏大造成。
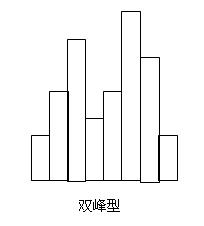
(3) 雙峰型
圖形出現兩個頂峰極可能是由於把不同加工者或不同材料、不同加工方法、不同設備生產的兩批產品混在一起形成的。
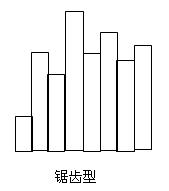
(4) 鋸齒型
圖形呈鋸齒狀參差不齊,多半是由於分組不當或檢測數據不准而造成。
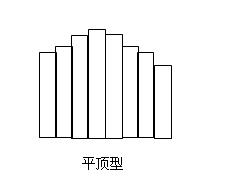
(5) 平頂型
無突出頂峰,通常由於生產過程中緩慢變化因素影響(如刀具磨損)造成。
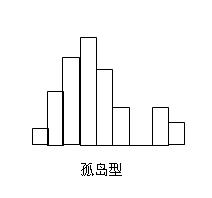
(6) 孤島型
由於測量有誤或生產中出現異常(原材料變化、刀具嚴重磨損等)。
4. 直方圖與標準界限比較
統計分佈符合標準的直方圖有以下幾種情況:
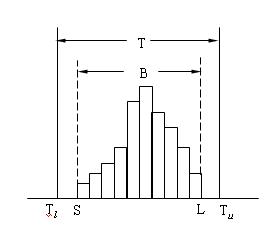
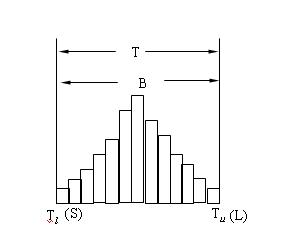
(1)理想直方圖:散佈範圍B在標準界限T=[Tl ,Tu]內,兩邊有餘量,
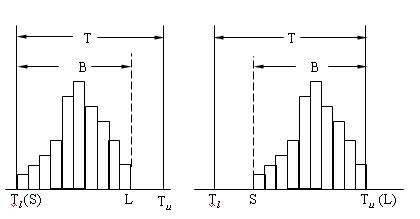
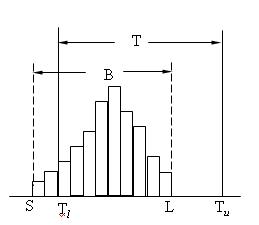
(2)B位於T內,一邊有餘量,一邊重合,分佈中心偏移標準中心,應採取措施使分佈中心與標準中心接近或重合,否則一側無餘量易出現不合格品。
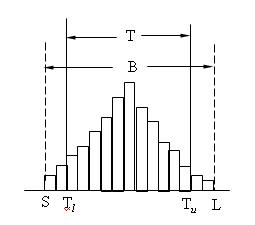
(3)B與T完全一致,兩邊無餘量,易出現不合格品。
統計分佈不符合標準的直方圖有以下幾種情況:
1.分佈中心偏移標準中心,一側超出標準界限,出現不合格品。
2.散佈範圍B大於T,兩側超出標準界限,均出現不合格品。
儘管直方圖能夠很好地反映出產品質量的分佈特征,但由於統計數據是樣本的頻數分佈,它不能反映產品隨時間的過程特性變化,有時生產過程已有趨向性變化,而直方圖卻屬正常型,這也是直方圖的局限性。
散佈圖是通過分析研究兩種因素的數據之間的關係,來控制影響產品質量的相關因素的一種有效方法。
有些變數之間有關係,但又不能由一個變數的數值精確地求出另一個變數的數值。將這兩種有關的數據列出,用點子打在座標圖上,然後觀察這兩種因素之間的關係。這種圖就稱為散佈圖。
如棉紗的水分含量與伸長度之間的關係;
噴漆時的室溫與漆料粘度的關係;
零件加工時切削用量與加工質量的關係;
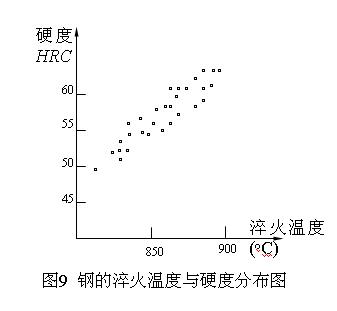
熱處理時鋼的淬火溫度與硬度的關係(如圖9)等等。
從圖9可見,數據的點子近似於一條直線,在這種情況下可以說硬度與淬火溫度近似線性關係。
從圖中可見,數據的點子近似於一條直線,在這種情況下可以說硬度與淬火溫度近似線性關係。
1.散佈圖的觀察分析
根據測量的兩種數據做出散佈圖後,觀察其分佈的形狀和密疏程度,來判斷它們關係密切程度。
散佈圖大致可分為下列情形:
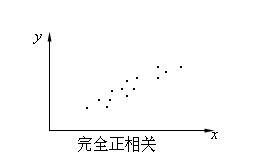
(1)完全正相關
x增大,y也隨之增大。x與y之間可用直線y=a+bx(b為正數)表示。
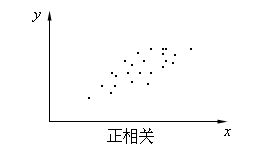
(2)正相關
x增大,y基本上隨之增大。此時除了因素x外,可能還有其它因素影響。
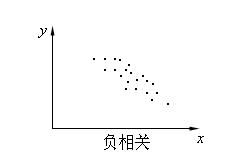
(3)負相關
x增大,y基本上隨之減小。同樣,此時可能還有其它因素影響。
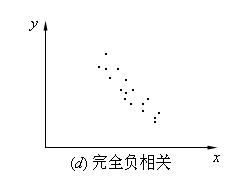
(4)完全負相關
x增大,y隨之減小。x與y之間可用直線y=a+bx(b為負數)表示。
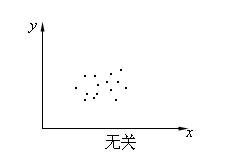
(5)無關
即x變化不影響y的變化。
製作與觀察散佈圖應註意的幾種情況
(a)應觀察是否有異常點或離群點出現,即有個別點子脫離總體點子較遠。
如果有不正常點子應剔除;
如果是原因不明的點子,應慎重處理,以防還有其它因素影響。
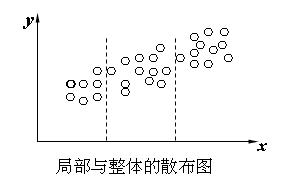
(b)散佈圖如果處理不當也會造成假象,如圖。
若將x的範圍只局限在中間的那一段,則在此範圍內看,y與x似乎並不相關,但從整體看,x與y關係還比較密切。
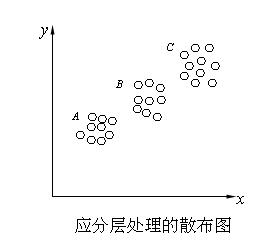
(c)散佈圖有時要分層處理。
如圖,x與y的相關關係似乎很密切,但若仔細分析,這些數據原是來自三種不同的條件。如果這些點子分成三個不同層次A、B、C。從每個層次中考慮,x與y實際上並不相關。
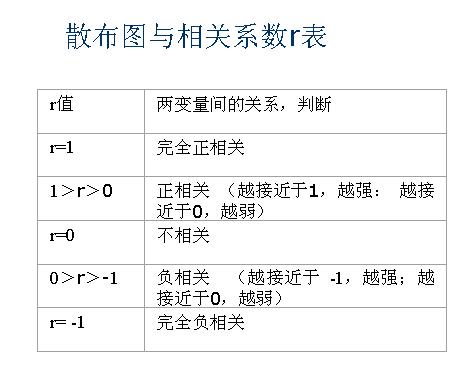
2.散佈圖與相關係數r
變數之間關係的密切程度,需要用一個數量指標來表示,稱為相關係數,通常用r表示。
不同的散佈圖有不同的相關係數,r滿足:-1≤r≤1。
因此,可根據相關係數r值來判斷散佈圖中兩個變數之間的關係。
相關係數的計算公式是:
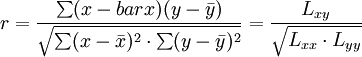
式中——表示n個x數據的平均值;
——表示n個y數據的平均值;
——表示x的離差平方之和,即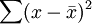
——表示y的離差平方之和,即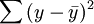
——表示x的離差與y的離差的乘積之和,即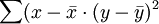
通常為了避免計算離差時的麻煩和誤差,在計算相關係數時,也可採用下列進行:
r=\frac{\sum xy-\frac{1}{n}(\sum x)(\sum y)}{\sqrt{\left[\sum x^2-\frac{1}{n}(\sum x)^2\right]\left[\sum y^2-\frac{1}{n}(\sum y)^2\right]}}
註意
r所表示線性相關。
當r的絕對值很小甚至等於0時,並不表示x與y之間就一定不存在任何關係。如x與y之間雖然是有關係的,但是經過計算相關係數的結果卻為0。這是因為此時x與y的關係是曲線關係,而不是線性關係造成的。
排列圖是通過找出影響產品質量的主要問題,以便改進關鍵項目。
排列圖最早由義大利經濟學家巴累特(Pareto)用於統計社會財富分佈狀況的。他發現少數人占有大部分財富,而大多數人卻只有少量財富,即所謂“關鍵的少數與次要的多數”這一相當普遍的社會現象。。
排列圖的形式
1.排列圖的作圖步驟
(1)確定分析對象
一般指不合格項目、廢品件數、消耗工時等等。
(2)收集與整理數據
可按廢品項目、缺陷項目,不同操作者等進行分類。列表彙總每個項目發生的數量即頻數fi,按大小進行排列。
(3)計算頻數fi、頻率Pi%、累計頻率Fi等。
(4)畫圖
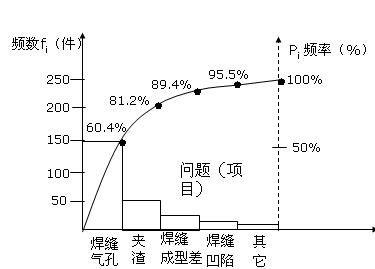
排列圖由兩個縱坐標,一個橫坐標。左邊的縱坐標表示頻數fi,右邊的縱坐標表示頻率Pi;橫坐標表示質量項目,按其頻數大小從左向右排列;各矩形的底邊相等,其高度表示對應項目的頻數。
(5)根據排列圖,確定主要、有影響、次要因素。
主要因素——累計頻率Fi在0~80%左右的若幹因素。它們是影響產品質量的關鍵原因,又稱為A類因素。其個數為1~2個,最多3個。
有影響因素——累計頻率Fi在80~95%左右的若幹因素。它們對產品質量有一定的影響,又稱為B類因素。
次要因素——累計頻率Fi在95~100%左右的若幹因素。它們對產品質量僅有輕微影響,又稱為C類因素
某化工廠對十五台尿素塔焊縫缺陷所需工時進行統計分析,如表9。
例3:某化工廠對十五台尿素塔焊縫缺陷所需工時進行統計分析,如表9。
按排列圖作圖步驟,確定焊縫氣孔和夾渣為主要因素;焊縫成型差和焊道凹陷為有影響因素,其它為次要因素。
2.排列圖的用途
(1) 找出主要因素。
排列圖把影響產品質量的“關鍵的少數與次要的多數”直觀地表現出來,使我們明確應該從哪裡著手來提高產品質量。實踐證明,集中精力將主要因素的影響減半比消滅次要因素收效顯著,而且容易得多。所以應當選取排列圖前1~2項主要因素作為質量改進的目標。如果前1~2項難度較大,而第3項簡易可行,馬上可見效果,也可先對第3項進行改進。
(2)解決工作質量問題也可用排列圖。
不僅產品質量,其它工作如節約能源、減少消耗、安全生產等都可用排列圖改進工作,提高工作質量。檢查質量改進措施的效果。採取質量改進措施後,為了檢驗其效果,可用排列圖來核查。如果確有效果,則改進後的排列圖中,橫坐標上因素排列順序或頻數矩形高度應有變化。
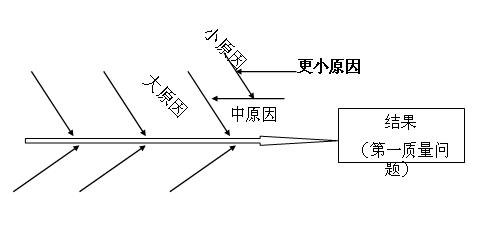
收集各種信息,比較原因大小和主次,找出產生問題的主要原因;也就是根據反映出來的主要問題(最終結果),找出影響它的大原因、中原因、小原因、更小原因等等。
主幹箭頭所指的為質量問題,主幹上的大枝表示大原因,中枝、小枝芽表示原因的依此展開。
1.因果圖作圖步驟
(1)確定要研究分析的質量問題和對象,既確定要解決的質量特性是什麼。將分析對象用肯定語氣(不標問號)寫在圖的右邊,最好定量表示,以便判斷採取措施後的效果。
(2)確定造成這個結果和質量問題的因素分類項目。影響工序質量的因素分為人員、設備、材料、工藝方法、環境等;再依次細分,畫大枝,箭頭指向主幹,箭尾端記上分類項目,並用方框框上。
(3)把到會者發言、討論、分析的意見歸納起來,按相互的相依隸屬關係,由大到小,從粗到細,逐步深入,直到能夠採取解決問題的措施為止。將上述項目分別展開:中枝表示對應的項目中造成質量問題的一個或幾個原因;一個原因畫一個箭頭,使它平行於主幹而指向大枝;把討論、意見歸納為短語,應言簡意準,記在箭乾的上面或下麵,再展開,畫小枝,小枝是造成中枝的原因。如此展開下去,越具體越細緻,就越好。
(4)確定因果圖中的主要、關鍵原因,並用符號明顯的標出,再去現場調查研究,驗證所確定的主要、關鍵原因是否找對、找準。以此作為制訂質量改進措施的重點項目。一般情況下,主要、關鍵原因不應超過所提出的原因總數的三分之一。
(5)註明本因果圖的名稱、日期、參加分析的人員、繪製人和參考查詢事項。
做因果圖的一個重要內容就是要收集大量的信息,而許多信息是靠人們主觀想象和思維得到的。
2.作因果圖的註意事項
(1)要充分發揚民主,把各種意見都記錄、整理入圖。一定要請當事人、知情人到會併發言,介紹情況,發表意見。
(2)主要、關鍵原因越具體,改進措施的針對性就越強。主要、關鍵原因初步確定後,應到現場去落實、驗證主要原因,在訂出切實可行的措施去解決。
(3)不要過分的追究個人責任,而要註意從組織上、管理上找原因。實事求是的提供質量數據和信息,不互相推托責任。
(4)儘可能用數據反映、說明問題。
(5)作完因果圖後,應檢查下列幾項:圖名、應標明主要原因是哪些等、文字是否簡便通俗、編譯是否明確、定性是否準確、應儘可能地定量化、改進措施不宜畫在圖上。
(6)有必要時,可再畫出措施表。
控製圖是判斷和預報生產過程中質量狀況是否發生波動的一種有效方法。
例如:美國某電氣公司的一個工廠有3千人,制定了5千張控製圖;
美國柯達彩捲公司有5千人,制定控製圖有3萬5千張,平均每人7張。
我國某飛機製造廠中的先進質量體系(AQS)中,要求一些工序必須作控製圖。
控製圖原理
- 質量具有波動性
- 5M1E(工序質量因素)
- 人(Man)、機器(Machine)、方法 (Method)、
- 材料(Material)、測量(Measure)、環境(Environment)
市場(Markets)
資金(Money)
動機(Motivation)
人(Man)、
機器和機械化(Machines and Mechanization)、
現代信息方法(Modem information methods) 、
材料(Materials)、
產品規格要求(Mountingproduct requirement )
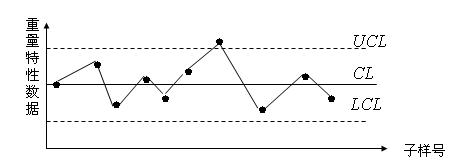
1.控製圖的基本格式
控製圖的基本格式如圖所示。
中心線CL(Central Line)——用細實線表示;
上控制界限UCL(Upper Cortrol Limit)——用虛線表示;
下控制界限LCL(Lower Control Limit)——用虛線表示。
所謂控製圖的基本思想就是把要控制的質量特性值用點子描在圖上,若點子全部落在上、下控制界限內,且沒有什麼異常狀況時,就可判斷生產過程是處於控制狀態。否則,就應根據異常情況查明並設法排除。通常,點子越過控制線就是報警的一種方式。
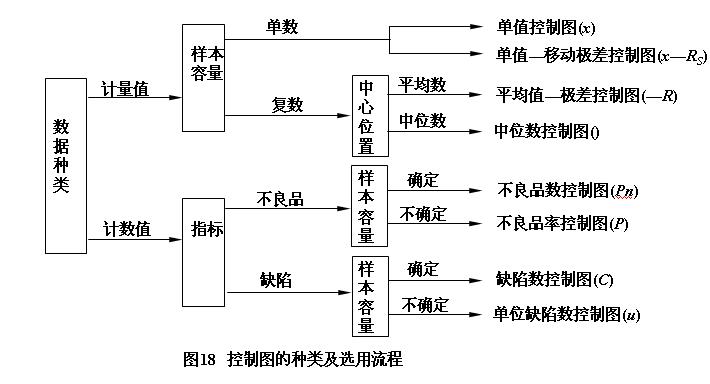
控製圖作為一種管理圖,在工業生產中,根據所要控制的質量指標的情況和數據性質分別加以選擇。
2.常用控製圖的種類
常用質量控製圖可分為兩大類:
(1)計量值控製圖包括:
單值控製圖( ),中位數控製圖。
),中位數控製圖。
(2)計數值控製圖包括:
不良品數控製圖,
不良品率控製圖,
缺陷數控製圖,
單位缺陷數控製圖。
根據所要控制的質量特性和數據的種類、條件等,按圖中得箭頭方向便可作出正確的選用。
計量值控製圖一般適用於以計量值為控制對象的場合。
計量值控製圖對工序中存在的系統性原因反應敏感,所以具有及時查明並消除異常的明顯作用,其效果比計數值控製圖顯著。計量值控製圖經常用來預防、分析和控制工序加工質量,特別是幾種控製圖的聯合使用。
計數值控製圖則用於以計數值為控制對象的場合。離散型的數值,比如,一個產品批的不合格品件數。雖然其取值範圍是確定的,但取值具有隨機性,只有在檢驗之後才能確定下來。
計數值控製圖的作用與計量值控製圖類似,其目的也是為了分析和控制生產工序的穩定性,預防不合格品的發生,保證產品質量。
3.控制界限的原理
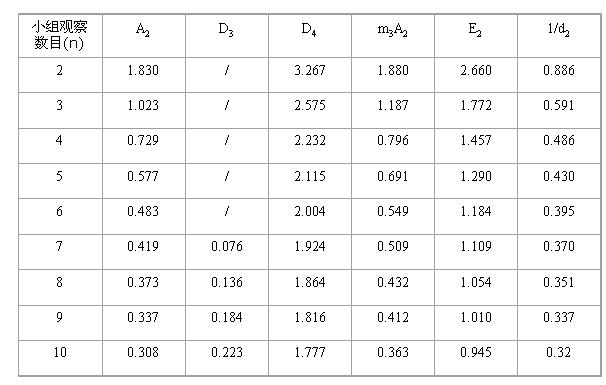
控製圖中的上、下控制界限,一般是用“三倍標準偏差法”(又稱3σ法)。而把中心線確定在被控制對象(如平均值、極差、中位數等)的平均值上。再以中心線為基準向上或向下量3倍標準偏差,就確定了上、下控制界限。另外,在求各種控製圖時,3倍標準偏差並不容易求到,故按統計理論計算出一些近似繫數用於各種控製圖的計算信息輸入表11
統計過程式控制制(SPC,)指的是,應用數理統計學的方法監視和調整過程作業或工序的技術(美國生產與庫存控制學會APICS,2002),是一種有效的質量保證、缺陷預防和控制的工程技術與方法。
統計質量控制(SQC,Statistical Quality Contr01)指的是,為了控制質量而應用的統計技術。通常這一術語可以同SPC互換使用,但是SQC所包含的含義比SPC更廣泛,即SQC包括了接受採樣和統計過程式控制制(APICS,2002)。所以,雖然SQC與SPC兩個術語可以互換使用,但SQC的含義更為廣泛。
SPC與SQC既有聯繫又有區別,SQC是一個總括的術語,它包含SPC,同時也包括產品驗收技術規則所使用的概率抽樣方法。
SQC與SPC共同所使用的輔助技術是:
①使用排列圖和檢查表確定一個問題的主要因素;
②使用因果圖展示出不良及缺陷的一系列的原因及其後果;
③使用直方圖和散佈圖辨認確定生產過程變數的分佈類型和數量。
SPC不僅僅是質量控制的一種技術方法,同時,它也是現場開展群眾性質量管理的一種方法,國外有些企業通常是組織3-13人的統計工序控制小組,開展質量控制活動。










總體來說不錯。