利率期限結構

出自 MBA智库百科(https://wiki.mbalib.com/)

利率期限結構（Term Structure of Interest Rates）

　　嚴格地說，利率期限結構是指某個時點不同期限的即期利率與到期期限的關係及變化規律。

　　由於零息債券的到期收益率等於相同期限的市場即期利率，從對應關係上來說，任何時刻的利率期限結構是利率水平和期限相聯繫的函數。因此，利率的期限結構，即零息債券的到期收益率與期限的關係可以用一條曲線來表示，如水平線、向上傾斜和向下傾斜的曲線。甚至還可能出現更複雜的收益率曲線，即債券收益率曲線是上述部分或全部收益率曲線的組合。收益率曲線的變化本質上體現了債券的到期收益率與期限之間的關係，即債券的短期利率和長期利率表現的差異性。

　　利率的期限結構理論說明為什麼各種不同的國債即期利率會有差別，而且這種差別會隨期限的長短而變化。

　　1、預期假說

　　利率期限結構的預期假說首先由歐文·費歇爾(Irving Fisher)(1896年)提出，是最古老的期限結構理論。

　　預期理論認為，長期債券的現期利率是短期債券的預期利率的函數，長期利率與短期利率之間的關係取決於現期短期利率與未來預期短期利率之間的關係。如果以E_t(r(s))表示時刻t對未來時刻的即期利率的預期，那麼預期理論的到期收益可以表達為：

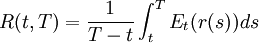
　　因此，如果預期的未來短期債券利率與現期短期債券利率相等，那麼長期債券的利率就與短期債券的利率相等，收益率曲線是一條水平線；如果預期的未來短期債券利率上升，那麼長期債券的利率必然高於現期短期債券的利率，收益率曲線是向上傾斜的曲線；如果預期的短期債券利率下降，則債券的期限越長，利率越低，收益率曲線就向下傾斜。

　　這一理論最主要的缺陷是嚴格地假定人們對未來短期債券的利率具有確定的預期；其次，該理論還假定，資金在長期資金市場和短期資金市場之間的流動是完全自由的。這兩個假定都過於理想化，與金融市場的實際差距太遠。

　　2、市場分割理論

　　預期假說對不同期限債券的利率之所以不同的原因提供了一種解釋。但預期理論有一個基本的假定是對未來債券利率的預期是確定的。如果對未來債券利率的預期是不確定的，那麼預期假說也就不再成立。只要未來債券的利率預期不確定，各種不同期限的債券就不可能完全相互替代，資金也不可能在長短期債券市場之間自由流動。

　　市場分割理論認為，債券市場可分為期限不同的互不相關的市場，各有自己獨立的市場均衡，長期借貸活動決定了長期債券利率，而短期交易決定了獨立於長期債券的短期利率。根據這種理論，利率的期限結構是由不同市場的均衡利率決定的。市場分割理論最大的缺陷正是在於它旗幟鮮明地宣稱，不同期限的債券市場是互不相關的。因為它無法解釋不同期限債券的利率所體現的同步波動現象，也無法解釋長期債券市場的利率隨著短期債券市場利率波動呈現的明顯有規律性的變化。

　　3、流動性偏好假說

　　希克思首先提出了不同期限債券的風險程度與利率結構的關係，較為完整地建立了流動性偏好理論。

　　根據流動性偏好理論，不同期限的債券之間存在一定的替代性，這意味著一種債券的預期收益確實可以影響不同期限債券的收益。但是不同期限的債券並非是完全可替代的，因為投資者對不同期限的債券具有不同的偏好。範·霍恩(Van Home)認為，遠期利率除了包括預期信息之外，還包括了風險因素，它可能是對流動性的補償。影響短期債券被扣除補償的因素包括：不同期限債券的可獲得程度及投資者對流動性的偏好程度。在債券定價中，流動性偏好導致了價格的差別。

　　這一理論假定，大多數投資者偏好持有短期證券。為了吸引投資者持有期限較長的債券，必須向他們支付流動性補償，而且流動性補償隨著時間的延長而增加，因此，實際觀察到的收益率曲線總是要比預期假說所預計的高。這一理論還假定投資者是風險厭惡者，他只有在獲得補償後才會進行風險投資，即使投資者預期短期利率保持不變，收益曲線也是向上傾斜的。如果R(t，T)是時刻T到期的債券的到期收益，E_t(r(s))是時刻t對未來時刻即期利率的預期，L(s，T)是時刻T到期的債券在時刻s的瞬時期限溢價，那麼按照預期理論和流動性偏好理論，到期收益率為：

　　利率期限結構模型按模型中包含的隨機因數的個數可分為單因數模型和多因數模型。

　　單因數模型中只含有一個隨機因數，意味著收益曲線上各點的隨機因數完全相關。多因數期限結構模型涉及多個隨機因數，表明收益曲線上不同點上的隨機因數具有某種程度的相關性。這種分類方法簡單明瞭，併為學術界廣泛接受。除了這種分類方法以外，還可以按照利率期限結構模型的均衡基礎來分類，即無套利機會模型和一般均衡模型。

　　1、一般均衡模型和無套利機會模型及其比較

　　主要的均衡模型有瓦西塞克模型(Vasicek)、CIR模型和雙平方根模型。這三個模型的瞬時短期利率滿足的隨機微分方程是：

胡和李模型：dr(t) = θ(t)dt + adw(t)，σ是正常數， 。

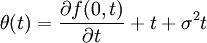布萊克—卡拉辛斯基模型：din(r(t)) = [θ(t) − α(t)tn(r(t))] + σ(t)dw(t) 。

HJM模型：df(t,T) = σ(t,T)dt + σ(t,T,f(t,T))dw(t) 。

　　這裡w(t)是標準布朗運動。胡和李模型中的偏導數表示時間t到期的初始遠期利率曲線f(0,t)的斜率。正是這個時間參變數函數使得胡和李模型定價的債券價格與所觀察到的市場債券價格相吻合。但這個期限結構模型沒有均值回覆的性質，而且利率取負值的概率大於0。著名的布萊克(Black)和卡拉辛斯基(Karasinski)(1991)對數正態利率期限結構模型中的θ(t)、α(t)、σ(t)都是時間參變數的確定性函數，這些參數的選取要求使模型精確地擬合初始利率期限結構和市場波動曲線。由於模型中含有利率的對數，不僅消除了利率取負值的可能性，而且它讓利率遠離了零利率值。赫斯、加羅和墨頓模型(HJM)中的 (t,T)和α(t,T,f(t,T))是時間T到期的遠期利率趨勢繫數和擴散繫數。

　　雖然均衡模型直接給定短期利率的動態演變過程，但它並不要求根據期限結構模型推定的零息債券的價格必須符合市場價格。為什麼允許模型的推定價格與債券的市場價格之間存在差異呢？這主要是因為影響債券價格的因素並不僅僅是短期利率。而無套利機會模型雖然也給定利率期限結構動態演變過程，但它要求模型給定的期限結構必須符合市場當時的利率期限結構。因此，只要正確給定無套利期限結構模型，那麼根據模型對零息債券的定價，必定符合當時的市場價格，否則將存在套利機會。

　　從兩類模型取得資料的角度來說，均衡模型主要利用過去的歷史資料進行統計分析，對模型的趨勢繫數和波動結構繫數進行估計，得出債券的價格和利率的期限結構動態演變。而無套利機會模型則需要即期利率期限結構的資料，這些資料很容易取得，而且無套利機會模型可以根據市場利率期限結構的資料及時進行調整。所以，均衡模型很適合於對債券的價格和利率的期限結構的動態過程進行預測。研究人員可以利用均衡模型瞭解期限結構曲線的形狀與將來經濟狀況的預測的關係，但無法保證利用歷史資料建立的期限結構模型能夠符合後來的實際演變過程。而無套利機會模型可以直接應用於市場交易，因為理論模型的債券價格和利率期限結構與市場的債券價格和利率期限結構是一致的。

　　從兩類模型的內部一致性來看，一般均衡模型的參數是通過長期積累的歷史資料進行統計分析、估計得來的，因此模型的趨勢繫數、波動結構繫數和均值回覆值不會每天變化，參數值能夠保持一定的穩定性，即使根據市場的變化重新註入新的市場資料，也不會對趨勢參數和波動參數值的大小造成顯著的影響，這樣均衡模型能夠在一段時間里保持一定的連貫性。而無套利機會模型需要假設趨勢變數、波動率結構和利率回覆均值，但是在兩個不同的時間，模型所設定的參數不大可能保持前後一致性，除非利用市場資料本身調整的參數恰好符合某種一致性。因為無套利機會模型需要根據市場條件的變化經常校正，也就是說需要經常調整參數，使零息債券的模型推定價格曲線和市場價格曲線以及模型的利率期限結構曲線和市場期限結構曲線的擬合達到最佳程度。

　　2、單因數模型和多因數模型的比較

　　前述的均衡模型和無套利機會模型都是單因數模型。單因數模型形式簡便，參數的個數少，容易估計，並且應用起來也比較簡單。

　　但單因數模型的缺陷也很明顯：

　　1）單因數模型的靈活性較差， 難以反映實際的各種可能的零息債券的收益曲線和利率期限結構的動態。因為單因數模型只將影響利率動態過程的一個因素包含到模型中，這顯然與現實不符。經濟學家經過研究發現，至少需要三個因數才能充分解釋利率的變化。利特曼(Litterman)和斯格因克曼(Scheinkman)的研究表明單個因數(短期利率)大約只能解釋美國國債利率變化的90％。傑姆希迪安(Jamshidian)和朱(Zhu)利用主成分分析方法或者因素分析方法，以日元、美元和德國馬克的數據資料，對整個收益曲線的歷史資料分析表明，兩個主成分因數只能解釋收益曲線變化的85％~90％，一個主成分因數可以解釋收益曲線總的變化的68％~76％ ，而三個主成分因數可以解釋收益曲線總的變化的93％ ~94％。

　　2）單因數模型隱含地假定所有可能的零息債券利率之間是完全相關的。

　　3）利用單因數模型對短期債券定價的誤差是比較小的。但如果用單因數模型對較長期限的債券定價就會出現比較大的誤差，此時用多因數模型進行定價比較合適。一般而言，由單因數模型推定的理論價格與實際的市場價格的誤差都將超過l％ ，這是勉強可以接受的；但如果用單因數模型對衍生證券定價時，其誤差將達到20％ 一30％，就讓人無法接受了。

　　多因數模型假定利率期限結構的動態演變過程是由幾個因數共同推動的。這些因數可以是巨集觀經濟的衝擊或者收益曲線本身的狀況，如收益水平、收益曲線的斜度和收益曲線的曲度，也可以是短期利率、短期利率的波動和長期利率等。主要的多因數模型有郎恩斯塔夫和斯瓦茲雙因數模型、布瑞安和斯瓦茲雙因數模型、斯切法(Schaefer)、安娜·雅各布森·施瓦茨（Anna Jacobson Schwartz）的斯切法和斯瓦茲模型、切恩三因數模型和巴爾杜茨三因數模型。

　　但是多因數模型的缺點也是很明顯的：

　　1、由於多因數模型中包括大量的參數，因此，建立一個多因數模型的工作量極為繁重，對參數進行估計和校準也是極為困難的。

　　2、模型的形式複雜，參數很多，要推出債券價格的明確的計算公式往往很困難，有時甚至是不可能的，因此，用替代函數對收益曲線進行擬合時，需要累次執行誤差最小化程式。

　　3、利用多因數模型給衍生證券定價時，一般要用數值計算方法才能得出衍生產品如期權的價格，只有朗恩斯塔夫和斯瓦茨雙因數模型能夠推出以到期時間、執行價格等表示的期權價格計算公式。

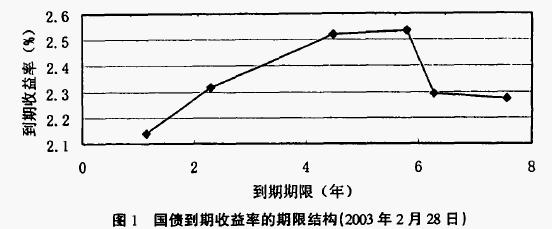
　　在固定收益證券的投資領域，利率期限結構分析是一個重要的手段。根據中國人民銀行公佈的債券到期收益率的計算公式可以得到我國國債的實際收益率期限結構。我國國債期限結構分析中選取的國債品種包括99國債5、00國債7、01國債2、01國債14、02國債6、02國債7等。這些國債品種在2003年2月28日的收益率曲線，如下圖1所示：

　　這種收益率曲線用預期假說無法解釋清楚，也不能用流動性偏好理論解釋清楚。流動性偏好理論假定投資者是風險厭惡型的，他們都偏好持有短期證券。因此，要讓投資者投資長期債券，必須向投資者支付流動性補償。這意味著長期利率等於短期利率與流動性補償之和。因此，按照預期理論或者流動性偏好理論只能解釋收益率期限結構向上傾斜、向下傾斜和水平的情況。但這種現象可以用市場分割理論解釋。

　　市場分割理論認為，債券市場是由期限不同的互不相關的市場組成，這些市場的利率由各自獨立的市場供求決定。因此，不同期限的債券就不可能完全相互替代，資金也不會在長短期債券市場之間自由流動。這樣，由於不同期限的債券的供求狀況存在差異，那麼按照債券的到期期限長短得到的流動性補償將形成一個不規則的序列。這個不規則的流動性補償序列結合短期利率，就會形成中間隆起的收益率期限結構曲線。

　　選取1998年1月到2003年2月間的銀行間國債回購市場的l周、2周和4周國債回購利率回歸得到三個瓦西塞克模型：

l周模型：dr(t)：2.0ll548(0.022496-r(t))+0.010703*dw(t)

2周模型：dr(t)=1.570225(0.021726-r(t))+0.008424*dw(t)

4周模型：dr(t)=1.07l929(O.019679-r(t))+0.005865*dw(t)

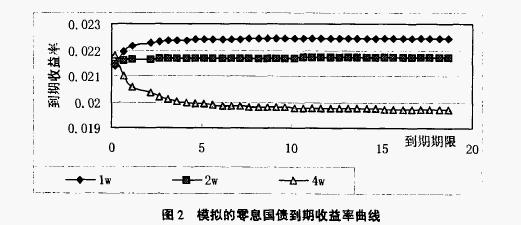
　　根據l周、2周和4周國債回購利率模型模擬的零息債券收益率期限結構曲線如圖2：

　　圖2中從上到下分別是根據l周、2周和4周國債回購利率的回歸模型模擬的零息債券期限結構。根據l周模型模擬的零息債券收益率曲線是緩慢上升的，根據2周模型模擬的零息債券收益率曲線近似於一條水平線，而根據4周模型模擬的零息債券收益率曲線是緩慢下降的，這代表了符合預期理論的三種典型收益率曲線。這可能是我國國債市場上不同的投資群體中存在三種不同的預期，這與預期理論假定人們對未來短期利率有確定的預期不符；也可能意味著我國國債市場上存在市場分割，不同的市場上有不同的預期。從回歸模型本身看，l周模型的均值回覆速度和短期利率的波動繫數最大，說明1周國債回購利率的波動最劇烈；4周國債回購利率的均值回覆速度和波動繫數最小，說明4周國債回購利率的波動最緩慢。

　　期限結構模型模擬和實際國債收益率曲線說明我國國債市場存在市場分割現象。怎樣解釋中國國債市場存在的市場分割現象呢?我國債券市場上，國債的期限結構過於單一，一年以下的短期國債和lO年以上的長期國債所占的比例太小，絕大部分國債的期限都是1年到lO年的中期國債。而不同的投資者對不同期限的國債有不同的投資偏好，在市場上找不到符合自己偏好的投資期限的國債時，這種投資需求將轉移到其它期限的國債。這種需求轉移將造成某些期限的國債的投資需求出奇地高，其直接結果是這類國債的價格上升到一定的高度，使它的到期收益率降低到低於其它期限的國債，甚至使流動性補償難以彌補因投資需求大幅度上升引致的到期收益率降低的幅度。此外，我國交易所市場和銀行間國債市場的不統一也是造成市場分割的原因之一。

　　要解決這個問題必須從幾個方面人手。首先，要建立一個統一的國債市場，將現有的銀行間市場和交易所市場統一起來，消除投資者進入市場的障礙。這樣可以充分釋放市場競爭力，使國債利率水平真實反映國債市場的資金供求狀況。其次，改革現有的國債發行期限不合理的狀況，長中短各期限國債要搭配發行，改變國債發行時間過於集中的狀況，借鑒美國的做法，每周發行國債，有利於形成完整的國債收益率曲線。

• 利率風險結構