無套利機會模型

出自 MBA智库百科(https://wiki.mbalib.com/)

無套利機會模型(Arbitrage-free Model)

　　無套利機會模型是指利用當前的債券市場價格推導出短期利率的未來演變過程，無套利機會模型推導出的結果必須符合當時的利率期限結構。

　　該類模型引入了利率的二項式變動，是在利率波動的約束條件下尋求利率的運行軌跡。Hoand Lee(1986)認為任何期限的利率水準都等於短期期限的利率水準加上或減去某種隨機衝擊，從而形成一個預期利率樹。由於Ho—Lee模型關於各種利率水準發生的相對頻率呈正態分佈和利率的波動不受利率水準影響的假設不切實際，隨後出現了一些修正模型，如OriginalSalomonBrothers模型(布魯斯，1999)、Black—Derman—Toy模型(Blacketc．，1990)和Black—Karasinski模型(Black and Karasinski，1991)。無套利機會模型主要是基於預期理論建立起來的模型。它們認為債券市場價格是合理的，並將利率期限結構視為既定，故缺乏持續性。

　　無套利機會模型定價的過程是，以觀察到的當時的利率期限結構為模型的輸入，假設短期利率的隨機過程，由零息債券到期時價值依次向前推算，得出每一期的債券價格，同時可以得出債券期權的價格。

　　(1)Ho和Lee模型(1986年)

　　Ho和Lee在1986年的論文中首先提出了期限結構的無套利模型。他們用債券的二叉樹圖的形式提出了該模型。模型有兩個參數：短期利率的標準差和該短期利率風險的市場價格。模型的結構為：

　　dr = θ(t)dt + σdw

　　其中，短期利率的瞬態標準差σ是常數，而θ(t)是為了保證模型與初始期限結構一致而選擇的時間的函數。

　　在Ho和Lee模型中，貼現債券和基於貼現債券的歐式期權可以求出解析解。用短期利率表示的t時間的貼現債券價格的表達式是：

　　P(t,T) = A(t,T)e ^{− r(t)(T − t)}

　　其中：

　　Ho和Lee模型的優點是它是可解析處理的馬爾科夫模型，它的應用簡便而且能精確地符合當前的利率期限結構。模型的缺點是：①在選擇標準差時給予使用者的靈活性太小，所有即期和遠期利率都具有相同的瞬態標準差σ；②不具有均值回覆性，這意味著在某個特定時點上，不論利率多麼高或多麼低，利率在下一個短時間內移動的平均方向總是一樣的。

　　(2)原始的所羅門兄弟模型(1987年)

　　在原始的所羅門兄弟模型(original Saloman brother model)中，新利率等於原有利率乘以一個隨機衝擊。因此，這個模型是以“乘法”而不是“加法”來處理隨機衝擊的。這將以對數正態分佈取代正態分佈，同時剋服了Ho—Lee模型中利率可能為負的缺陷。

　　該模型的結構為：

　　dlnr = m(t)dt + σdw

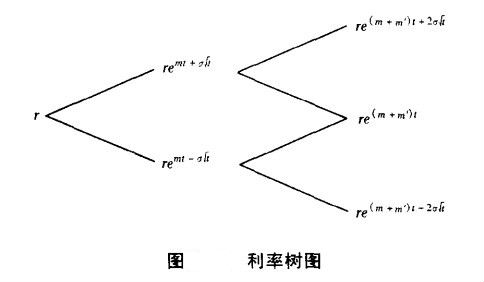
　　其中，m(t)是關於時間t的趨勢變數。短期利率的演變過程如圖所示。

　　模型中的參數σ稱為“比例波動率”，m'是下一時刻的m(t)。短期利率的實際波動率等於比例波動率乘以當時的短期利率，表明短期利率的波動率隨利率變化而變化，並不是如Ho-Lee模型中假設為常數。

　　原始的所羅門兄弟模型的優點是：①用對數分佈取代正態分佈，剋服了Ho—Lee模型中利率可能為負的缺陷；②短期利率的波動率與利率成正比，並不是常數。許多業內人士認為假設比例波動率為常數優於假設短期利率的波動率為常數(如：Ho—Lee模型)。該模型的缺點是沒有反映現實生活中的利率均值回覆現象。

　　(3)Black—Derman—Toy模型(1990年)

　　相對於所羅門模型來說，Black—Derman—Toy模型的最主要的優點是可以反映利率期限結構的實際波動情況。這是因為它假設短期利率波動率將隨時間而變動，而利率的趨勢變數m將受到利率水準的影響。

　　許多研究者認為，當利率水準偏高時，它的趨勢變數(drift，指m的數字而言)相對較小，甚至為負值；當利率水準偏低時，趨勢變數相對較大。換言之，他們相信利率具有均值回歸性。

　　Black—Derman—Toy模型具有均值回覆的性質，但這個性質是通過波動率的期限結構而顯現的。換言之，趨勢變數受到利率水準的影響程度，完全取決於短期利率的演變過程。這種方法有一個缺點，即以不精確的方式呈現均值回覆的性質，主要依靠估計短期利率的未來波動率來近似實現均值回覆。這種不精確性可能對模型的定價功能產生不利的影響。所以，模型或許應該在不受波動率過程的影響下，單獨考慮回歸均數的性質。

　　模型的結構：

　　其中，θ'是下一個時間段短期利率r的瞬時標準差。這個模型與其他無套利機會模型一樣，它對於零息債券所定的價格必須等於市場價格。可是，在波動率的期限結構方面，這個模型所提供的結果可以符合實際的情況，為了達到這個目的，Black—Derman—Toy模型允許短期利率的波動率隨著時間而變動，所以這種波動率又稱為“區域性波動率”。然而，隨著時間而變動的區域性波動率會引起一些問題，因為利率可能呈現非結合性的樹狀圖。樹狀圖無法結合，解決的辦法是，讓上行與下行狀況的未來發展各具不同的趨勢變數。

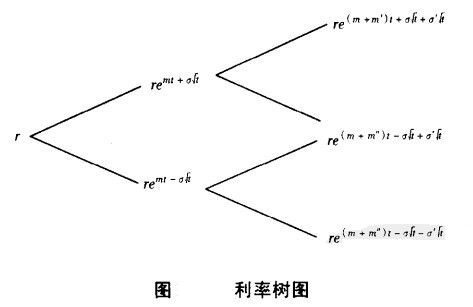
　　假定m'代表由上行狀態發展的趨勢變數，m''代表由下行狀態發展的趨勢變數，則短期利率的樹狀圖將如圖所示。

　　如果“上行-下行狀況”與“下行-上行狀況”的利率相等，樹狀圖便會結合：因而設定：

　　這相當於

　　即趨勢變數完全由短期利率的波動率來決定，從而實現均值回覆。

　　Black—Derman—Toy模型的優點是：①利率波動率隨時間而變動，優於假設為常數；②具有均值回覆特性：缺點是：趨勢變數完全由短期利率的波動率來決定，這種方式也是不精確的，模型應該在不受波動率過程的影響下，單獨考慮均值回覆的性質。

　　(4)Black—Karasinski模型(1990年)

　　Black—Karasinski模型是以明顯的方式來處理均值回覆，它假設短期利率有一個中央傾向，並設定短期利率回歸中央傾向的速度。這個模型可以從數種不同的角度來建立。可以設定均值回覆的某些合理參數值，或設定均值回覆的速度為某一常數，然後調整模型中的其他參數，讓利率期限結構與波動率的期限結構能夠相互協調。或者，也可以設定區域性波動率的參數值，然後凋整其他參數值，讓利率期限結構與波動率的期限結構能夠相互協調、第三種方法是原作者所建議的方法，它以市場的某組數值來套入模型，其中以差價上限選擇權曲線(differential cap curve)(差價上限選擇權是根據某名義金額，支付短期利率與履約利率的差價(如果這項差價為正值))尤其實用。將差價上限選擇權的價格套入模型中，並倒推模型的參數值，這是希望模型在確定其他或然性合約的價格時，便能夠反映市場的實際情況。

　　模型的結構：

　　dlnr = Φ(t)[lnμ(t) − lnr]dt + σ(t)dw

　　其中：μ(t)是目標利率(target rate)，Φ(t)表示均值回覆，σ(t)表示區域波動率，即lnr的波動率。

　　Black—Karasinski模型的優點：①允許獨立設定均值回覆的行為；②由於它足對數正態分佈的模型，利率水準不可能為負，利率的波動率與利率的水準成比例。缺點足利率的樹狀圖仍呈現非結合性的樹狀圖，均值回覆的行為將受到波動率結構的影響。

　　(5)Hull和White模型(1990年)

　　Hull和White在1990年、1993年的論文中提出了自己的模型，他們的模型主要是對Vasicek和CIR模型進行了擴展，在短期利率模型中加入了依賴時間t的參數θ(t)。他們認為考慮時間因素是合理的，因為經濟的景氣迴圈、人們對將來貨幣政策及其他巨集觀經濟變數的預期都與時間有關。

　　他們建議的Vasicek模型的擴展形式是：

　　dr = [θ(t) + a(t)(b − r)]dt + σ(t)dw

　　很顯然，當a=0、θ(t)常數時，該模型就是Ho—Lee模型。

　　利用ITO定理，得出債券價格的微分方程，求解微分方程，可以求得債券價格的解析式：

　　P(t,T) = A(t,T)e ^{− B(t,T)t(t)}

　　其中：

　　他們建議的CIR模型的擴展形式是：

　　同樣，也給出了相應的零息債券價格表達式。

　　Hull和White模型的貢獻主要是對Vasicek和CIR模型進行了擴展，考慮了時間因素對利率的影響。

　　(6)HJM模型(Heath，Jarrow and Moaon)(1992年)

　　Heath、Jarrow和Morton等人建立了遠期利率的期限結構模型。在此之前的期限結構模型都是從假設債券價格或即期利率服從某種隨機過程人手的。Heath、Jarrow和Moron首先指出：在漂移率(drift)和瞬態遠期利率的標準差之間存在著某種聯繫。

　　模型結構：

　　其中f(t,T)表示在t時刻觀測到的T時刻到期合約的瞬態遠期利率，表示利率過去值、當前值和t時刻債券價格的矢量，α(·)和σ(·)分別表示遠期利率的瞬時均值和瞬時標準差。

　　Heath，Jarrow和Morton通過無套利定價原理導出了瞬態遠期利率的漂移率與波動率之間的關係，即：

　　這樣，只要通過估計瞬態遠期利率的波動率，就可得到遠期利率的漂移率：也就是說，不必估計漂移率，就可以求出債券的價格。

　　通過遠期利率模型可以求得短期利率的隨機模型，這種短期利率的隨機模型與其他一些模型直接假設短期利率服從布朗運動不同，它是非馬爾科夫過程，可以用蒙特卡羅模擬方法來處理期限結構的一般非馬爾科夫過程，但耗時過久。

　　HJM模型的優點主要有：①與其他無套利模型一樣，符合當前的期限結構；②債券及其期權的價格由利率的波動率來決定，不必估計利率的漂移率；③不用假設投資偏好。缺點是短期利率樹圖不重合，一般用蒙特卡羅方法來模擬，計算起來要慢些。

　　(1)取得模型需要的資料不同。就有關利率風險的市場價格來說，無套利機會模型需要即期利率期限結構的資料，這些利率資料相對容易取得。均衡模型卻需要以某種方法宋衡量投資者承擔利率風險所要求的報酬，這方面的資料遠較即期利率難以取得，通常必須以統計方法來分析過去的價格與利率走勢。所以，就取得模型所需要的資料來說，無套利模型顯然具有優勢。

　　(2)對資料缺陷的敏感程度不同。無套利機會模型將即期利率期限結構模型視為合理，實際上，某些市場報價並不合理，這可能是因為計算卜的錯誤、市場流動性或其他特殊因素所造成的。無套利機會模型會將這類的資料缺陷納入定價模型中，可是，均衡模型會剔除這類有問題的價格，這也正是該類模型的特色。

　　(3)模型的持續性不同。每當運用的時候，無套利機會模型需要假設趨勢變數、波動率與利率均值回覆的行為。可是，在兩個不同的運用日期，模型所設定的數據沒有持續性。舉例來說，在某一天，模型所採用的趨勢變數將涵蓋未來的20年，但使用者知道，明天必須運用今天的利率期限結構的資料，重新設定趨勢變數。總之，無套利機會模型缺乏持續性、相反，均衡模型是根據歷史資料或某些堅定的信念來設定參數，所以模型的參數不會每

• 一般均衡理論