HJM模型

出自 MBA智库百科(https://wiki.mbalib.com/)

　　HJM(Heath-Jarrow-Morton)模型由赫斯（Heath）、加羅（Jarrow）和墨頓（Morton）在1992年提出，T 時刻瞬時遠期利率f(t,T)的變化服從：

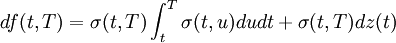
　　因此整個模型估計的參數只有一個，即波動性，而且這個波動性不會隨著測度的變化而 變化。

　　HJM 模型的主要方法是無套利分析法，即在n個因數風險模型下，可以通過一個無風險資產和n個風險資產的組合構造資產市場上的所有資產。

　　給定債券波動率的期限結構，就可以得到債券定價的全部信息，它是無套利模型的基準模型。但是模型本身在應用的過程中也會產生問題。在構造利率變動的二叉數或者三叉數模型時，利率通常在上升和下降後就不會再重新聚合。也就是說，利率先上升後下降與先下降後上升之後所達到的不是同一個節點，利率變動不是馬爾可夫鏈。這就會導致二叉樹模型的最終節點的幾何擴大，極大地增加計算和模擬的難度。

　　1、HJM模型只需要規定遠期利率的波動結構和初始遠期利率曲線就足以刻畫期限結構的動態，這樣也就不需要估計趨勢繫數。

　　2、HJM模型不需要考慮投資者的個人偏好，避免了與效用相關的參數，而其它模型需要計算風險的市場價格。

　　3、HJM模型刻畫期限結構的方法是用遠期利率的波動結構刻畫遠期利率，進而再刻畫瞬時現期利率。

　　HJM模型也有一些不足之處：

　　1、瞬時遠期利率不是直接可觀察的，因此要應用HJM模型就可能比較困難。

　　2、HJM框架中，瞬時遠期利率的連續複合排除了出現對數正態過程的可能性。