蒙特卡羅方法
出自 MBA智库百科(https://wiki.mbalib.com/)
蒙特卡羅方法(Monte Carlo method)
目錄 |
蒙特卡羅方法又稱統計模擬法、隨機抽樣技術,是一種隨機模擬方法,以概率和統計理論方法為基礎的一種計算方法,是使用隨機數(或更常見的偽隨機數)來解決很多計算問題的方法。將所求解的問題同一定的概率模型相聯繫,用電子電腦實現統計模擬或抽樣,以獲得問題的近似解。為象徵性地表明這一方法的概率統計特征,故借用賭城蒙特卡羅命名。
1946年,美國拉斯阿莫斯國家實驗室(Los Alamos National Lab)的三位科學家John von Neumann(馮諾依曼),Stan Ulam(斯坦烏爾姆)和Nick Metropolis(尼克梅特珀利斯)共同發明,被稱為蒙特卡洛方法。具體定義是:在廣場上畫一個邊長一米的正方形,在正方形內部隨意用粉筆畫一個不規則的形,現在要計算這個不規則圖形的面積,蒙特卡洛(Monte Carlo)方法告訴我們,均勻的向該正方形內撒N(N是一個很大的自然數)個黃豆,隨後數數有多少個黃豆在這個不規則幾何形狀內部,比如說有M個,那麼,這個奇怪形積與正方形的面積之比便近似於M/N,N越大,算出來的值便越精確。在這裡我們要假定豆子都在一個平面上,相互之間沒有重疊。
舉例說明,一個有10000個整數的集合,要求其中位數,可以從中抽取m<10000個數,把它們的中位數近似地看作這個集合的中位數。隨著m增大,近似結果是最終結果的概率也在增大,但除非把整個集合全部遍歷一邊,無法知道近似結果是不是真實結果。
另外一個例子,給定數N,要求它是不是素數,可以任選m個小於N的數,看其中有沒有能整除N的數,如果沒有則判斷為素數。這和通常見到的蒙特卡羅例子不同,近似結果往往錯得更離譜,但隨著m增大,近似結果是最終結果的概率也在增大。
把蒙特卡羅方法和另外一類方法——拉斯維加斯方法對比一下,更容易瞭解哪些方法屬於蒙特卡羅,哪些不屬於。拉斯維加斯方法是另一類隨機方法的統稱。這類方法的特點是,隨著採樣次數的增多,得到的正確結果的概率逐漸加大,如果隨機採樣過程中已經找到了正確結果,該方法可以判別並報告,但在但在放棄隨機採樣,而採用類似全採樣這樣的確定性方法之前,不保證能找到任何結果(包括近似結果)。
舉例說明,有一個有死衚衕但無環路的迷宮,要求從入口走到出口的一條路徑。可以從入口出發,在每個叉路口隨機選擇一個方向前行,到死衚衕則報告失敗並回到入口重新試探,到出口則報告成功。隨著試探次數增多,找到一條入口到出口的路徑的概率增大,但除非全枚舉,即使試10000年,也無法保證找到任何要求的路徑。
20世紀40年代,第二次世界大戰中美國研製原子彈的“曼哈頓計劃”計劃成員S.M.烏拉姆和J.馮·諾伊曼首先提出蒙特卡羅方法(MonteCarlo Method)。該計劃的主持人之一、數學家數學家馮·諾伊曼用馳名世界的賭城——摩納哥的MonteCarlo來命名這種方法,為它蒙上了一層神秘色彩。蒙特卡羅方法(Monte Carlo Method)的創始人主要是四位美國人:Stanislaw Marcin Ulam(烏拉姆,波蘭裔數學家)、Enrico Fermi(恩里科·費米,義大利裔物理學家)、Johnvon Neumann(約翰·馮·諾伊曼,電腦結構奠基人)和Nicholas ConstantineMetropolis(尼古拉斯·康斯坦丁·美特普利斯,希臘裔數學家)。
現代的統計模擬方法最早由數學家烏拉姆提出,被Metropolis(美特普利斯)命名為蒙特卡羅方法,蒙特卡羅是著名的賭場,賭博總是和統計密切關聯的,所以這個命名風趣而貼切,很快被大家廣泛接受。被不過據說費米之前就已經在實驗中使用了,但是沒有發表。烏拉姆(Stanislaw Marcin Ulam)是波蘭裔美籍數學家,早年是研究拓撲的,後因參與曼哈頓工程,興趣遂轉嚮應用數學,他首先提出用蒙特卡羅方法(Monte Carlo Method)解決計算數學中的一些問題,然後又將其應用到解決鏈式反應的理論中去,在美國洛斯阿拉莫斯國家實驗室(Los Alamos NationalLab)研究裂變物質的中子連鎖反應的時候,開始使用統計模擬的方法,併在最早的電腦上進行編程實現,是蒙卡MC方法的奠基人。義大利裔美國人恩里科·費米(Enrico Fermi)是個物理大牛,理論和實驗同時都是大牛,這在物理界很少見,但英年早逝(上帝都嫉妒)。約翰·馮·諾伊曼(John von Neumann)是電腦界的牛頓,發明電腦硬體著名的馮諾依曼架構,也是非常厲害,結果和Fermi一樣英年早逝(被上帝嫉妒死了)。尼古拉斯·美特普利斯(Nicholas Metropolis)是希臘裔美籍數學家、物理學家、電腦科學家,對Monte Carlo方法做的貢獻相當大,1953年他和別人共同提出模擬退火演算法(SimulatedAnnealing),使得Monte Carlo方法得到廣泛應用,Metropolis一生主要的貢獻就是Monte Carlo方法,很專一;他碩士畢業於BSc (1937) and PhD(1941)博士畢業,生於Born: Jun 11, 1915, Chicago,IL,逝於Died: Oct 17, 1999, LosAlamos, NM,活了84歲,是這四個人里唯一長壽的科學家。
蒙特卡羅(Monte Carlo)方法的基本思想很早以前就被人們所發現和利用。在這四人發明現代統計模擬方法,即蒙特卡羅方法(Monte Carlo Method)之前,類似蒙特卡羅方法的演算法就已經存在。早在17世紀,人們就知道用事件發生的“頻率”來決定事件的“概率”。蒙特卡羅方法的源頭,可以追溯到18世紀,布豐當年用於計算π的著名的投針實驗就是蒙特卡羅模擬實驗。1777年,法國數學家布豐(Georges Louis Leclerede Buffon, 1707-1788)提出用投針實驗的方法求圓周率π,共投針2212次,與直線相交的有704次,2212÷704≈30142,得數是圓周率π的近似值,後來他把實驗寫進他的論文《或然性算術嘗試》[4]。這被認為是蒙特卡羅方法的起源。19世紀人們用投針試驗的方法來決定圓周率π。統計採樣的方法其實數學家們很早就知道,但是在電腦出現以前,隨機數生成的成本很高,所以該方法也沒有實用價值。隨著電腦技術在二十世紀後半葉的迅猛發展,隨機模擬技術很快進入實用階段。類比到深度學習,算力對演算法的推動也是非常明顯,令人感嘆!~對那些用確定演算法不可行或不可能解決的問題,蒙特卡羅方法常常為人們帶來希望。
Monte Carlo方法的基本思想很早以前就被人們所發現和利用。早在17世紀,人們就知道用事件發生的“頻率”來決定事件的“概率”。19世紀人們用投針試驗的方法來決定圓周率π。本世紀40年代電子電腦的出現,特別是近年來高速電子電腦的出現,使得用數學方法在電腦上大量、快速地模擬這樣的試驗成為可能。
考慮平面上的一個邊長為1的正方形及其內部的一個形狀不規則的“圖形”,如何求出這個“圖形”的面積呢?Monte Carlo方法是這樣一種“隨機化”的方法:向該正方形“隨機地”投擲N個點,有M個點落於“圖形”內,則該“圖形”的面積近似為M/N。 可用民意測驗來作一個不嚴格的比喻。民意測驗的人不是徵詢每一個登記選民的意見,而是通過對選民進行小規模的抽樣調查來確定可能的優勝者。其基本思想是一樣的。
科技計算中的問題比這要複雜得多。比如金融衍生產品(期權、期貨、掉期等)的定價及交易風險估算,問題的維數(即變數的個數)可能高達數百甚至數千。對這類問題,難度隨維數的增加呈指數增長,這就是所謂的“維數的災難”(Curse of Dimensionality),傳統的數值方法難以對付(即使使用速度最快的電腦)。Monte Carlo方法能很好地用來對付維數的災難,因為該方法的計算複雜性不再依賴於維數。以前那些本來是無法計算的問題現在也能夠計算量。為提高方法的效率,科學家們提出了許多所謂的“方差縮減”技巧。
另一類形式與Monte Carlo方法相似,但理論基礎不同的方法—“擬蒙特卡羅方法”(Quasi-Monte Carlo方法)—近年來也獲得迅速發展。我國數學家華羅庚、王元提出的“華—王”方法即是其中的一例。這種方法的基本思想是“用確定性的超均勻分佈序列(數學上稱為Low Discrepancy Sequences)代替Monte Carlo方法中的隨機數序列。對某些問題該方法的實際速度一般可比Monte Carlo方法提出高數百倍,並可計算精確度。
由概率定義知,某事件的概率可以用大量試驗中該事件發生的頻率來估算,當樣本容量足夠大時,可以認為該事件的發生頻率即為其概率。因此,可以先對影響其可靠度的隨機變數進行大量的隨機抽樣,然後把這些抽樣值一組一組地代入功能函數式,確定結構是否失效,最後從中求得結構的失效概率。蒙特卡羅法正是基於此思路進行分析的。
設有統計獨立的隨機變數Xi(i=1,2,3,…,k),其對應的概率密度函數分別為fx1,fx2,…,fxk,功能函數式為Z=g(x1,x2,…,xk)。
首先根據各隨機變數的相應分佈,產生N組隨機數x1,x2,…,xk值,計算功能函數值 Zi=g(x1,x2,…,xk)(i=1,2,…,N),若其中有L組隨機數對應的功能函數值Zi≤0,則當N→∞時,根據伯努利大數定理及正態隨機變數的特性有:結構失效概率,可靠指標。
從蒙特卡羅方法的思路可看出,該方法迴避了結構可靠度分析中的數學困難,不管狀態函數是否非線性、隨機變數是否非正態,只要模擬的次數足夠多,就可得到一個比較精確的失效概率和可靠度指標。特別在岩土體分析中,變異繫數往往較大,與JC法計算的可靠指標相比,結果更為精確,並且由於思路簡單易於編製程式。
蒙卡法與一般計演算法有很大區別,一般計算方法對於解決多維或因素複雜的問題非常困難,而蒙卡法對於解決這方面的問題卻比較簡單。使用MC方法的特點及其優缺點:
①直接追蹤粒子,物理思路清晰,易於理解。
②採用隨機抽樣的方法,較真切的模擬粒子輸運的過程,反映了統計漲落的規律。
③不受系統多維、多因素等複雜性的限制,是解決複雜系統粒子輸運問題的好方法。
④MC程式結構清晰簡單。
⑤研究人員採用MC方法編寫程式來解決粒子輸運問題,比較容易得到自己想得到的任意中間結果,應用靈活性強。
MC方法主要弱點是收斂速度較慢和誤差的概率性質,其概率誤差正比於,如果單純以增大抽樣粒子個數N來減小誤差,就要增加很大的計算量。
可用民意測驗來作一個不嚴格的比喻。民意測驗的人不是徵詢每一個登記選民的意見,而是通過對選民進行小規模的抽樣調查來確定可能的優勝者。其基本思想是一樣的。科技計算中的問題比這要複雜得多。比如金融衍生產品(期權、期貨、掉期等)的定價及交易風險估算,問題的維數(即變數的個數)可能高達數百甚至數千。對這類問題,難度隨維數的增加呈指數增長,這就是所謂的“維數的災難”(CourseDimensionality),傳統的數值方法難以對付(即使使用速度最快的電腦)。MC方法能很好地用來對付維數的災難,因為該方法的計算複雜性不再依賴於維數。以前那些本來是無法計算的問題現在也能夠計算量。為提高方法的效率,科學家們提出了許多所謂的“方差縮減”技巧。
另一類形式與Monte Carlo方法相似,但理論基礎不同的方法——“擬蒙特卡羅方法”(Quasi-MonteCarlo Method)近年來也獲得迅速發展。我國數學家華羅庚、王元提出的“華-王”方法即是其中的一例。這種方法的基本思想是“用確定性的超均勻分佈序列(數學上稱為LowDiscrepancy Sequences)代替Monte Carlo方法中的隨機數序列。對某些問題該方法的實際速度一般可比Monte Carlo方法提出高數百倍,並可計算精確度。
通常蒙特·卡羅方法通過構造符合一定規則的隨機數來解決數學上的各種問題。對於那些由於計算過於複雜而難以得到解析解或者根本沒有解析解的問題,蒙特·卡羅方法是一種有效的求出數值解的方法。一般蒙特·卡羅方法在數學中最常見的應用就是蒙特·卡羅積分。
蒙特卡羅演算法表示採樣越多,越近似最優解。舉個例子,假如筐里有100個蘋果,讓我每次閉眼拿1個,挑出最大的。於是我隨機拿1個,再隨機拿1個跟它比,留下大的,再隨機拿1個……我每拿一次,留下的蘋果都至少不比上次的小。拿的次數越多,挑出的蘋果就越大,但我除非拿100次,否則無法肯定挑出了最大的。這個挑蘋果的演算法,就屬於蒙特卡羅演算法。告訴我們樣本容量足夠大,則最接近所要求解的概率。
蒙特卡羅方法在金融工程學,巨集觀經濟學,生物醫學,計算物理學(如粒子輸運計算、量子熱力學計算、空氣動力學計算)等領域應用廣泛。
在解決實際問題的時候應用蒙特·卡羅方法主要有兩部分工作:
1. 用蒙特·卡羅方法模擬某一過程時,需要產生各種概率分佈的隨機變數。
2. 用統計方法把模型的數字特征估計出來,從而得到實際問題的數值解。
使用蒙特·卡羅方法進行分子模擬計算是按照以下步驟進行的:
1. 使用隨機數發生器產生一個隨機的分子構型。
2. 對此分子構型的其中粒子坐標做無規則的改變,產生一個新的分子構型。
3. 計算新的分子構型的能量。
4. 比較新的分子構型與改變前的分子構型的能量變化,判斷是否接受該構型。
- 若新的分子構型能量低於原分子構型的能量,則接受新的構型,使用這個構型重覆再做下一次迭代。
- 若新的分子構型能量高於原分子構型的能量,則計算玻爾茲曼因數,並產生一個隨機數。
- 若這個隨機數大於所計算出的玻爾茲曼因數,則放棄這個構型,重新計算。
- 若這個隨機數小於所計算出的玻爾茲曼因數,則接受這個構型,使用這個構型重覆再做下一次迭代。
5. 如此進行迭代計算,直至最後搜索出低於所給能量條件的分子構型結束。
蒙特卡羅方法是以概率統計原理為基礎,模擬事物的形成過程,以達到認識事物特征及其變化規律的方法。這種方法的前提假設是不確定性參數可以用概率分佈來描述。蒙特卡羅方法實施步驟:
1、通過敏感性分析,確定隨機變數;
2、構造隨機變數的概率分佈模型;
3、為各輸入隨機變數抽取隨機數;
4、將抽得的隨機數轉化為各輸入隨機變數的抽樣值;
5、將抽樣值組成一組項目評價基礎數據;
6、根據基礎數據計算出評價指標值;
7、整理模擬結果所得評價指標的期望值、方差、標準差和它的概率分佈及累計概率,繪製累計概率分佈圖,計算項目可行或不可行的概率。
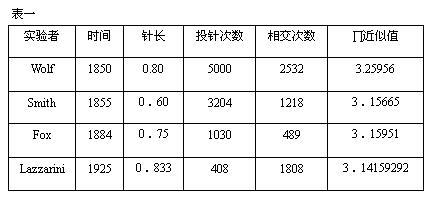
從理論上來說,蒙特卡羅方法需要大量的實驗。實驗次數越多,所得到的結果才越精確。以上Buffon的投針實驗為例、歷史上的記錄如下表1。
從表中數據可以看到,一直到公元20世紀初期,儘管實驗次數數以千計,利用蒙特卡羅方法所得到的圓周率∏值,還是達不到公元5世紀祖沖之的推算精度。這可能是傳統蒙特卡羅方法長期得不到推廣的主要原因。
電腦技術的發展,使得蒙特卡羅方法在最近10年得到快速的普及。現代的蒙特卡羅方法,已經不必親自動手做實驗,而是藉助電腦的高速運轉能力,使得原本費時費力的實驗過程,變成了快速和輕而易舉的事情。它不但用於解決許多複雜的科學方面的問題,也被項目管理人員經常使用。
藉助電腦技術,蒙特卡羅方法實現了兩大優點:
一是簡單,省卻了繁複的數學報導和演算過程,使得一般人也能夠理解和掌握;
二是快速。簡單和快速,是蒙特卡羅方法在現代項目管理中獲得應用的技術基礎。
蒙特卡羅方法有很強的適應性,問題的幾何形狀的複雜性對它的影響不大。該方法的收斂性是指概率意義下的收斂,因此問題維數的增加不會影響它的收斂速度,而且存貯單元也很省,這些是用該方法處理大型複雜問題時的優勢。因此,隨著電子電腦的發展和科學技術問題的日趨複雜,蒙特卡羅方法的應用也越來越廣泛。它不僅較好地解決了多重積分計算、微分方程求解、積分方程求解、特征值計算和非線性方程組求解等高難度和複雜的數學計算問題,而且在統計物理、核物理、真空技術、系統科學 、信息科學 、公用事業、地質、醫學,可靠性及電腦科學等廣泛的領域都得到成功的應用。
項目管理中蒙特卡羅模擬方法的一般步驟是:
1、對每一項活動,輸入最小、最大和最可能估計數據,併為其選擇一種合適的先驗分佈模型;
2、電腦根據上述輸入,利用給定的某種規則,快速實施充分大量的隨機抽樣;
3、對隨機抽樣的數據進行必要的數學計算,求出結果;
4、對求出的結果進行統計學處理,求出最小值、最大值以及數學期望值和單位標準偏差;
5、根據求出的統計學處理數據,讓電腦自動生成概率分佈曲線和累積概率曲線(通常是基於正態分佈的概率累積S曲線);
非權重蒙特卡羅積分,也稱確定性抽樣,是對被積函數變數區間進行隨機均勻抽樣,然後對被抽樣點的函數值求平均,從而可以得到函數積分的近似值。此種方法的正確性是基於概率論的中心極限定理。當抽樣點數為m時,使用此種方法所得近似解的統計誤差恆為 1除於根號M,不隨積分維數的改變而改變。因此當積分維度較高時,蒙特卡羅方法相對於其他數值解法更優。
案例一:蒙特卡羅模型在投資項目決策中的開發應用[1]
一、問題的提出
隨著社會主義市場經濟體制的逐步完善、經濟水平的逐步提高,我國社會經濟活動日趨複雜,越來越多變,其影響越來越廣泛,越來越深遠,不確定性逐漸成為企業決策時所面臨的主要難題。因此,如何在不確定條件下做出投資決策,就成為目前理論和實踐工作者們廣泛關註的一個核心課題。
傳統的投資評價理論——以凈現值法(NPV) 為代表的投資決策分析方法,其根本缺陷在於它們是事先對未來的現金流量做出估計,並假設其為不變或靜態的狀況,無法衡量不確定因素的影響,不能體現遞延決策以應對所帶來的管理彈性。所以,在不確定環境下的投資,用凈現值法評估項目不能體現柔性投資安排決策所體現的價值,無助於項目在決策中迴避風險。在多變的市場環境中,不確定性與競爭者的反應使實際收入與預期收入有所出入, 所以凈現值法(NPV) 適用於常規項目,未來不確定性比較小的項目。
為此理論界對未來投資環境不確定性大的項目提出了實物期權法,但在實踐中應用的還是比較少。實物期權法的應用對企業決策者的綜合素質要求比較高,對企業資源能力要求也比較高。但是實物期權法改變了我國管理者對戰略投資的思維方式。
基於以上的分析,我們得出這樣的結論:傳統的投資決策方法對風險項目和不確定性項目的評價有較多不完善之處,有必要對其改進;實物期權法理論上解決了傳統決策方法對不確定性項目評價的不足,但其應用尚處於體系不成熟階段,在實踐中應用並不廣泛。至此,引入蒙特卡羅模型的理論和其分析方法,此方法特別適用於參數波動性大,且服從某一概率分佈的項目,例如地質勘察、氣田開發等項目。
蒙特卡羅模型是利用電腦進行數值計算的一類特殊風格的方法, 它是把某一現實或抽象系統的某種特征或部分狀態, 用模擬模型的系統來代替或模仿, 使所求問題的解正好是模擬模型的參數或特征量, 再通過統計實驗, 求出模型參數或特征量的估計值, 得出所求問題的近似解。目前評價不確定和風險項目多用敏感性分析和概率分析,但計算上較為複雜,尤其各因素變化可能出現概率的確定比較困難。蒙特卡羅模型解決了這方面的問題,各種因素出現的概率全部由軟體自動給出,通過多次模擬,得出項目是否應該投資。該方法應用面廣, 適應性強。
惠斯通(Weston) 對美國1 000 家大公司所作的統計表明: 在公司管理決策中, 採用隨機模擬方法的頻率占29 % 以上, 遠大於其他數學方法的使用頻率 。特別, 該方法演算法簡單, 但計算量大, 在模擬實際問題時, 要求所建模型必須反覆驗證,這就離不開電腦技術的幫助, 自然可利用任何一門高級語言來實現這種方法。通過一案例具體實現了基於Excel 的Monte Carlo 模擬系統, 由於Microsof tExcel 電子錶格軟體強大的數據分析功能和友好的界面設計能力, 使系統實現起來頗感輕鬆自如。
二、理論和方法
蒙特卡洛模擬早在四十年前就用於求解核物理方面的問題。當管理問題更為複雜時,傳統的數學方法就難以進行了。模擬是將一個真實事物模型化,然後對該模型做各種實驗,模擬也是一個通過實驗和糾正誤差來尋求最佳選擇的數值性求解的過程。模擬作為一種有效的數值處理方法, 計算量大。以前只是停留在理論探討上, 手工是無法完成的。在管理領域由於規律複雜隨機因素多, 很多問題難以用線性數學公式分析和解決, 用模擬則有效得多。在新式的電腦普及後, 用模擬技術來求解管理問題已成為可能。
電腦模擬技術和其它方法相比有以下優點:
1) 成本低、風險小, 在產品未投產, 實際生產未形成就可以對市場進行分析模擬, 極大地減少費用和風險。
2) 環境條件要求低, 工作人員不需要高深的數學能力, 完全依靠電腦進行, 在硬體和軟體日益降價的情況下, 可以成為現實。
3) 可信度高, 常用的統計推理方法需要大量歷史數據(如平均數法、最小二乘法) , 對無歷史資料的場合就無能為力(如新產品) , 而且精度低。
模擬的最大特點是藉助一個隨機數來模模擬實的現實, 隨機數的產生則由電腦來產生。稱為偽隨機數。即:
Rn = F (r - 1 , r - 2 ,……r - k)
在以對象為中心的軟體中, EXCEL 有一個RANE()函數實現偽隨機數功能。RANE( )實際上是一個會自動產生偽隨機數的子程式。用產生的偽隨機數模擬市場購買行為, 得出產品銷售量, 在生產成本相對固定時進而推測出產品的利潤。此方法不用編製複雜的程式, 思路假設為, 作為系統內部是可以控制的, 即企業內部生產成本可以人為控制, 但系統外部因素是不可控制的(消費心理導致的消費行為) , 則生產與銷售就會產生矛盾。生產量小於銷售量, 造成開工不足資源浪費;生產量大於銷售量, 造成產品積壓, 資金占用, 同樣形成資源的浪費。最好生產量等於銷售量, 則資源浪費最小, 自然經濟效益就最高, 實際就是利潤最大化。如果能科學地測算出在什麼情況下利潤最大, 則這時的產量就是最佳產量, 成本也就最低。這就是市場作為導向, 以銷定產的公認市場經濟的準則。實際工作中, 很多產品的消費是具有隨機性的, 主要是一些需求彈性大、價格彈性大、價格低、與日常生活有關的中、小商品, 如副食品、日用消費品、玩具、輕工業產品。對企業而言利潤較高的產品。
從以上分析可以看出, 蒙特卡洛模擬可以動態實現對產品利潤的預測, 從而對產品產量科學控制,實現資源優化, 是一種較好的決策支持方法。
三、蒙特卡羅模型在Excel 表中的應用
某氣田投資項目期投資、壽命期、殘值以及各年的收入、支出,以及應付稅金的稅率、項目的資本成本等都是獨立的隨機變數,他們的概率密度函數如表1所示。
表 各變數對應概率密度函數表
| A | B | C | D | |
| 2 | 概率 | 對應的隨機數 | 可能值 | |
| 3 | 投資Yo | 0.2 | 0 | 450 |
| 4 | 0.5 | 20 | 500 | |
| 5 | 0.3 | 70 | 550 | |
| 6 | 壽命N | 0.5 | 0 | 6 |
| 7 | 0.3 | 50 | 7 | |
| 8 | 0.2 | 80 | 8 | |
| 9 | 殘值F | 0.25 | 0 | 40 |
| 10 | 0.5 | 25 | 50 | |
| 11 | 0.25 | 75 | 60 | |
| 12 | 稅率Te | 0.2 | 0 | 45 |
| 13 | 0.5 | 20 | 48 | |
| 14 | 0.3 | 70 | 51 | |
| 15 | 年收入R | 0.15 | 0 | 700 |
| 16 | 0.3 | 15 | 750 | |
| 17 | 0.4 | 45 | 800 | |
| 18 | 0.15 | 85 | 850 | |
| 19 | 年支出C | 0.2 | 0 | 100 |
| 20 | 0.4 | 20 | 150 | |
| 21 | 0.3 | 60 | 200 | |
| 22 | 0.1 | 90 | 250 | |
| 23 | 資本成本i | 0.1 | 0 | 10 |
| 24 | 0.2 | 10 | 12 | |
| 25 | 0.4 | 30 | 14 | |
| 26 | 0.2 | 70 | 16 | |
| 27 | 0.1 | 90 | 18 |
本案例用windowsXP 中的Excel2003 對該項目進行模擬如下:
1) 在A32 單元格(投資Yo 模擬:隨機數) 輸入:= RANDBETWEEN (0 ,99) ;在B32 單元格(投資Yo模擬:投資) 輸入: = VLOO KUP (A32 , $C $3 : $D$5 ,2) ;
2) 在C32 單元格(壽命N 模擬:隨機數) 輸入: =RANDBETWEEN (0 ,99) ;在D32 單元格(壽命N 模擬: 壽命) 輸入: = VLOO KUP ( C32 , $C $6 : $D$8 ,2) ;
3) E32 ,G32 , I32 , K32 ,M32 單元格分別輸入: =RANDBETWEEN (0 , 99) ; F32 = VLOOPUP ( E32 ,$C $9 : $D $11 , 2) , H32 = VLOOPUP ( G32 , $C$12 : $D $14 ,2) ,J 32 = VLOO KUP ( I32 , $C $15 :$D $18 ,2) ,L32 = VLOO KUP ( K32 , $C $19 : $D$22 ,2) ,
N32 = VLOO KUP(M32 , $C $23 : $D $27 ,2)
4) O32 = (B32 - F32) / D32 , P32 = (J 32 - L32 -O32) * (1 - H32/ 100) + O32 ,Q32 = PV (N32/ 100 ,D32 , - P32) - B32 ;
5) H3 = AVERA GE ( Q32 , Q5031 ) , H4 =STDEV (Q32 ,Q5031) ,H5 = MAX ( Q32 , Q5031 ) , H6 = MIN ( Q32 ,Q5031) ,H7 = H4/ H3 ,H8 = COUN TIF (Q32 :Q5031 ,“ < 0”) / COUN T(Q32 ,Q5031) 。
在Excel 工具表中模擬5000次,結果輸出見下表 :
表 結果輸出表(1)
| A | B | C | D | E | F | G | H | |
| 投資Yo模擬 | 壽命N模擬 | 殘值F模擬 | 稅率Te模擬 | |||||
| 隨機數 | 投資 | 隨機數 | 壽命 | 隨機數 | 殘值 | 隨機數 | 稅率 | |
| 32 | 17 | 450 | 78 | 7 | 51 | 50 | 2 | 45 |
| 33 | 31 | 500 | 84 | 8 | 87 | 60 | 67 | 48 |
| 34 | 22 | 500 | 63 | 7 | 97 | 60 | 88 | 51 |
| 35 | 95 | 550 | 70 | 7 | 40 | 50 | 81 | 51 |
| 36 | 31 | 500 | 96 | 8 | 20 | 40 | 12 | 45 |
| 37 | 16 | 450 | 1 | 6 | 41 | 50 | 66 | 48 |
| 38 | 79 | 550 | 33 | 6 | 87 | 60 | 51 | 48 |
| 39 | 0 | 450 | 97 | 8 | 78 | 60 | 17 | 45 |
| 40 | 35 | 500 | 43 | 6 | 22 | 40 | 5 | 45 |
| 41 | 3 | 450 | 70 | 7 | 52 | 50 | 87 | 51 |
| 42 | 78 | 550 | 39 | 6 | 69 | 50 | 30 | 48 |
| 43 | 20 | 500 | 36 | 6 | 90 | 60 | 2 | 45 |
| 44 | 96 | 550 | 5 | 6 | 92 | 60 | 40 | 48 |
| 45 | 51 | 500 | 36 | 6 | 90 | 60 | 20 | 48 |
| 46 | 58 | 500 | 39 | 6 | 1 | 40 | 11 | 45 |
| 47 | 4 | 450 | 79 | 7 | 22 | 40 | 29 | 48 |
| 48 | 83 | 550 | 36 | 6 | 40 | 50 | 62 | 48 |
| … | … | … | … | … | … | … | … | … |
表 結果輸出表(2)
| I | J | K | L | M | N | |
| 年收入R模擬 | 年支出C模擬 | 資本成本i模擬 | ||||
| 隨機數 | 年收入 | 隨機數 | 年支出 | 隨機數 | 資本成本 | |
| 32 | 12 | 700 | 88 | 200 | 4 | 10 |
| 33 | 11 | 700 | 88 | 200 | 59 | 14 |
| 34 | 3 | 700 | 79 | 200 | 7 | 10 |
| 35 | 68 | 800 | 20 | 150 | 77 | 16 |
| 36 | 23 | 750 | 21 | 150 | 53 | 14 |
| 37 | 98 | 850 | 73 | 200 | 40 | 14 |
| 38 | 37 | 750 | 23 | 150 | 99 | 18 |
| 39 | 72 | 800 | 92 | 250 | 16 | 12 |
| 40 | 81 | 800 | 96 | 250 | 46 | 14 |
| 41 | 32 | 750 | 17 | 100 | 74 | 16 |
| 42 | 70 | 800 | 73 | 200 | 17 | 12 |
| 43 | 39 | 750 | 78 | 200 | 68 | 14 |
| 44 | 12 | 700 | 46 | 150 | 92 | 18 |
| 45 | 79 | 800 | 75 | 200 | 15 | 12 |
| 46 | 10 | 700 | 52 | 150 | 54 | 14 |
| 47 | 45 | 800 | 1 | 100 | 87 | 16 |
| 48 | 75 | 800 | 47 | 150 | 4 | 10 |
| … | … | … | … | … | … | … |
表 結果輸出表(3)
| O | P | Q | |
| 折舊Dt | 各年現金流量Yt | NPV | |
| 32 | 75 | 307175 | 840.3314803 |
| 33 | 76166667 | 348.18 | 856.3672298 |
| 34 | 64128571 | 342.8571 | 1064.716528 |
| 35 | 75 | 374 | 878.0912297 |
| 36 | 55.71429 | 364.7429 | 1114.128559 |
| 37 | 62.185714 | 368.1714 | 986.8844068 |
| 38 | 73.33333 | 355.9 | 883.9767691 |
| 39 | 58.57143 | 299.3714 | 1007.465496 |
| 40 | 83.33333 | 336.5 | 689.9136332 |
| 41 | 83.33333 | 326 | 717.7056104 |
| 42 | 66.66667 | 344 | 964.3241193 |
| 43 | 85 | 35218 | 749.9748285 |
| 44 | 57.14286 | 347.6429 | 1040.798547 |
| 45 | 64.28571 | 276.4286 | 761.5527004 |
| 46 | 76.166667 | 348.8 | 785.2358848 |
| 47 | 48.75 | 335.4 | 1105.87495 |
| 48 | 57.5 | 391.6 | 1200.950194 |
| … | … | … | … |
所得結果如下:
表 凈現值模擬計算結果表
| F | G | H | |
| 2 | 凈現值模擬計算結果 | ||
| 3 | 凈現值期望值 | 952.13017 | |
| 4 | 凈現值標準差 | 198.90501 | |
| 5 | 凈現值最大值 | 1726.9833 | |
| 6 | 凈現值最小值 | 405.54502 | |
| 7 | 變異繫數 | 0.12089053 | |
| 8 | 凈現值為負的概率 | 0 | |
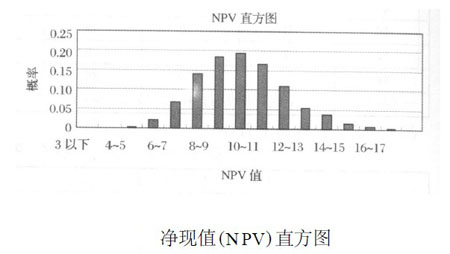
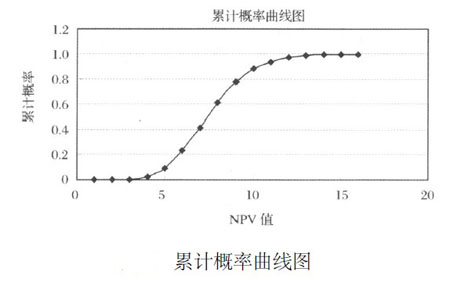
表 凈現值概率分佈統計表
| 凈現值概率分佈統計 | |||
| 系統分組 | 分佈區間 | 概率 | 累計概率 |
| 300 | 3 | 以下0 | 0 |
| 400 | 3~4 | 0 | 0 |
| 500 | 4~5 | 0.0036 | 0.0036 |
| 600 | 5~6 | 0.0244 | 0.028 |
| 700 | 6~7 | 0.062 | 0.09 |
| 800 | 7~8 | 0.1322 | 0.2222 |
| 900 | 8~9 | 0.1898 | 0.412 |
| 1000 | 9~10 | 0.1992 | 0.6112 |
| 1100 | 10~11 | 0.1628 | 0.774 |
| 1200 | 11~12 | 0.1162 | 0.8902 |
| 1300 | 12~13 | 0.0548 | 0.945 |
| 1400 | 13~14 | 0.0338 | 0.9788 |
| 1500 | 14~15 | 0.0132 | 0.992 |
| 1600 | 15~16 | 0.005 | 0.997 |
| 1700 | 16~17 | 0.0018 | 0.9988 |
| 1800 | 17以上 | 0.0012 | 1 |
從分析結果得出,雖然此項目未來的不確定性很大,但由圖可知,此氣田開發項目服從正態分佈,模擬5 000次的結果是凈現值為負的概率為零,並且項目的期望凈現值為952113 萬元,說明項目值得開發。
由以上的案例分析可知,基於蒙特卡羅模擬的風險分析,對於工程實際應用具有較強的參考價值。隨機模擬5 000 次,如果僅靠人的大腦進行計算,這在現實世界中是不可能的,但考慮到系統決策支持功能, 演算法設計為由使用者自己設計方案, 採用人機交互, 這樣可以發揮使用者的經驗判斷;系統實現模擬運算——系統對每一個設定的投資項目期投資、壽命期、殘值以及各年的收入、支出,以及應付稅金的稅率、項目的資本成本等隨機變數及他們的概率密度函數,通過蒙特卡羅模擬方法,得出了項目在不同概率發生的情況下凈現值模擬計算結果。為人們解決不確定性項目的決策提供了簡單的方法,節約了人們的工作量和時間。但是利用蒙特卡羅模型分析問題時,收集數據是非常關鍵的。
- ↑ 蒙特卡羅模型在投資項目決策中的開發應用[J].科技和產業,2009,9(11):119-123
本条目由以下用户参与贡献
蔓草寒烟,Vulture,Zfj3000,funwmy,Angle Roh,Dan,Lemonady,Junly,Yixi,泡芙小姐,KAER,连晓雾,Gaoshan2013,郝樱木,Tracy,Mis铭,林晓辰,LuyinT,Horizon,陈cc.評論(共18條)
謝謝 Junly 的補充,我先用了,回頭看能不能也補充點
添加了新的案例,希望對您有幫助!
有沒有 Excel 檔案可以下載?謝謝
有沒有 EXCEL 檔案可以下載? 如果是用來補強歷史數據的不足,只是模擬消費行為、模擬數據,本身不也需要自行假設?那有是怎麼來的?
大牛,在嗎?想請教一下,此氣田開發項目的項目的期望凈現值為952113 萬元,這個是如何計算的?
你自己把這些數據和公式複製到Excel里算一遍就明白了。








謝謝