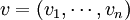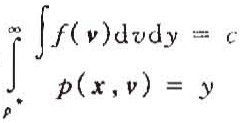投資決策分析
出自 MBA智库百科(https://wiki.mbalib.com/)
投資決策分析(investment decision analysis)
目錄 |
投資決策分析是對各種建設投資方案進行綜合分析。投資是為一定目的而預先墊付資金或實物的行為,又稱為固定資產投資。
投資決策分析包括投資規模決策分析、投資方向決策分析和工程項目投資決策分析。前兩者屬於巨集觀經濟範疇,後者屬於微觀經濟範疇。
(1)投資規模決策分析
社會的發展要求儘可能多地進行固定資產投資。但投資的供給能力受很多因素的制約,主要取決於國民收入的數量及其增長速度,積累基金和消費基金的分配比例,固定資產積累、流動資產積累和社會後備基金的分配比例,固定資產折舊率等。投資規模的決策分析就是以經濟發展戰略為指導,研究投資的供給能力,從而確定固定資產投資的數量、增長速度和戰線的長短。投資是一個較長的過程,在一定期間內要支出大量的勞動力和生產資料而不提供任何有效用的產品或服務,所以必須通過決策分析來確定固定資產投資的合理規模,以保證國民經濟的綜合平衡,人民生活的不斷改善和生產的正常進行,同時也為了保證固定資產投資的經濟效益。
(2)投資方向決策分析
投資方向決策分析就是以經濟發展戰略為指導,根據國民經濟有計劃按比例發展的客觀要求,確定固定資產投資在國民經濟各部門、各地區之間的分配比例。由於投資的分配比例決定著固定資產再生產的比例,從而在很大程度上決定著國民經濟產業結構、工業部門結構和工業佈局的合理性,所以投資方向的決策分析也是保證國民經濟綜合平衡和固定資產投資經濟效益的重要環節。
(3)工程項目投資決策分析
指對於待選工程項目及其各種投資方案進行評價比較,依據項目的可行性和預期的社會經濟效果而決定取捨的選擇過程。各國進行投資決策分析的經濟依據是不一樣的。在蘇聯,由國家頒佈基本建設投資經濟效果的標準計算方法。在西方,生產性項目一般由私人投資,採用財務報表分析法、償還期法和目前被認為是最有效的現金流量貼現方法進行企業財務評價;非生產性的公共工程項目一般由政府投資、評價方法採用成本效益分析或多目標決策。在發展中國家,由於價格失真、政府對私人投資的干預較多等原因,所以廣泛採用基於成本效益分析的各種評價方法。中國近年來引入的工程項目可行性研究方法中,作為投資決策主要依據的國民經濟評價方法就是一種成本效益分析方法。
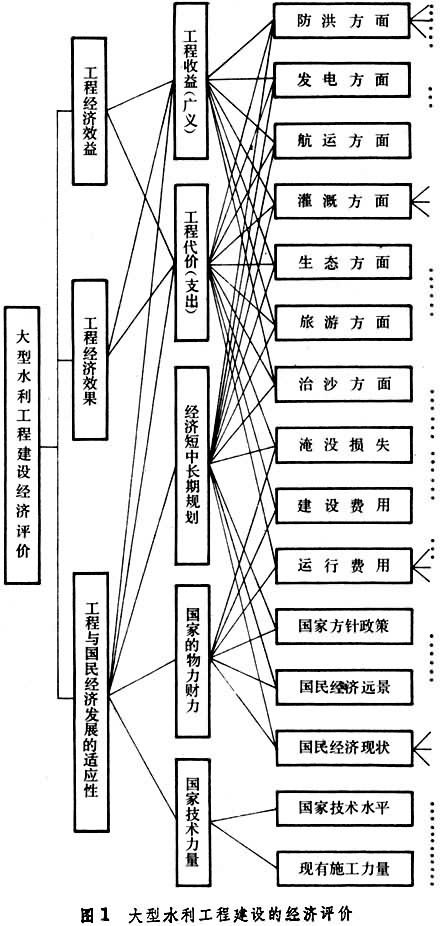
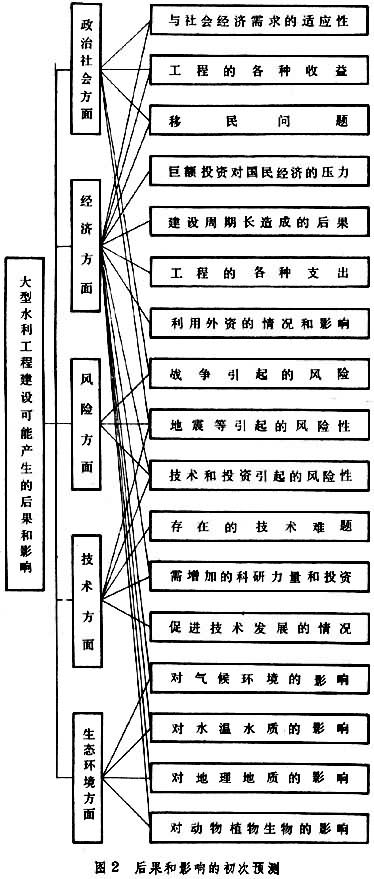
任何工程項目都是一個複雜的大系統,應用系統工程的方法時,首先要從系統整體出發,進行總體效益的分析。例如,對大型水利工程項目進行投資決策分析時,可能涉及防洪、發電、航運、灌溉、水產、旅游、治沙、防鹼、治澇等方面,要從政治、社會、經濟、技術和生態環境諸方面進行綜合評價(圖 1)。對於複雜的大型工程項目,不僅要弄清楚有哪些因素影響工程建設,而且要研究工程建設將會產生哪些後果和影響(圖 2),然後對工程方案進行綜合評價。最後要研究出一套決策方法,協助決策者在綜合評價的基礎上作出抉擇。為瞭解決大型工程建設的決策問題,一般是把定性分析與定量分析結合起來,為此要建立決策模型。
決策模型應滿足以下幾個方面的要求:
①能夠同時接受定性的信息和定量的信息,主觀的信息和客觀的信息;
②儘可能降低對指標評價精度的要求,以適應社會經濟系統的實際情況;
③適應於離散方案集的情況;
④便於集中多種不同的決策觀點,將個體決策與群決策結合起來。一般可採用目標規劃法、組合規劃法、多指標人機對話選優法等方法來建立決策模型。
投資決策分析的案例分析[1]
Markowitz證券組合理論的核心在於,選擇風險最小、收益最大的證券組合,其中收益用均值描述,而風險用方差描述由於越來越多的金融機構採用vaR測量市場風險,使用vaR作為風險限額,特別是監管當局也在使用vaR確定風險資本金,因此許多金融機構及其業務部門在做投資選擇時,往往需要滿足VaR約束.即給定一個VaR.要求確定收益最大的證券組合,並同時滿足vaR約束;或在市場條件變化情況下,在給定的vaR範圍內,獲得一個最優投資重組(重新平衡)策略,使得投資組合收益最大。
1.基於風險價值投資決策問題分析
首先給出相關變數的定義和說明.考慮由n種資產構成的資產集合,這些資產可以是股票、債券、期權等金融資產一個投資組合J由其在這些資產中的頭寸決定:
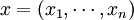
投資組合x在給定風險因數v下的價值為p(x,v),它是關於x和v的一個複雜非線性函數(甚至是不連續的)實際中p(x,v)可以表示為:
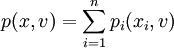
當組合中的資產都是股票時,可以簡化為頭寸與風險因數的線性組合形式:
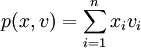
用v0表示t=0時風險因數的價值,t=1時風險因數的行為可由概率密度函數為f(v)的分佈描述,則在t=l時的投資組合的價值均由概率密度函數為尹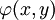 的分佈表示:
的分佈表示:
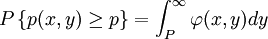
用風險因數的概率密度函數f(v)和投資組合的價值函數p(x,y)表示,就是:
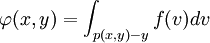
在實際中尋找這一分佈函數極為困難,特別是當投資組合包含數以百計的資產或p(x,y)為非線性形式時但研究關於該分佈函數的逼近過程的文獻還是比較多。
現在給出投資組合x的VaR,用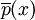 表示t=1時刻投資組合的期望價值:
表示t=1時刻投資組合的期望價值:
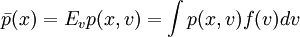
選擇置信水平c,p * 示組合的最小價值:
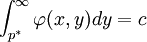 ,
,
則由相對vaR定義:
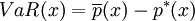
考慮投資組合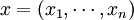 ,其中xi是第i種資產的投資權重,
,其中xi是第i種資產的投資權重,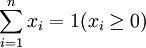 ,在這種情況下,需要解決的是下述問題:。
,在這種情況下,需要解決的是下述問題:。
問題:尋找使vaR
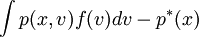
達到最小的投資組合x,它滿足下列條件:
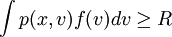 ,
,
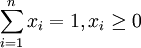
問題求解的典型演算法是梯度法。當p(x,v)關於(x,v)可微,梯度px(x,v)和pv(x,v)滿足Lipshitz條件,且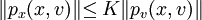 時,有
時,有
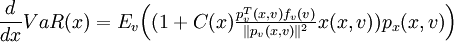
式中: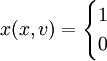 如果
如果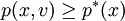 ,否則,
,否則,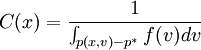
因此,VaR的梯度計算涉及3個變數的估計,即
p * (x)積分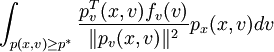 和
和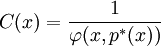 其中
其中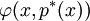 是投資組合的價值分佈函數在y = p * (x)處的密度,它可以在計算VaR時自然求得。
是投資組合的價值分佈函數在y = p * (x)處的密度,它可以在計算VaR時自然求得。
2.基於歷史風險價值的投資決策模型
我們考慮資產組合里所有金融資產為股票的情況,此時證券組合的收益率與組合的權重x成線性關係:。
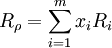 式中:Rρ為證券組合的收益率;Ri為第i種證券的期望收益率;m表示組合里有m種證券。
式中:Rρ為證券組合的收益率;Ri為第i種證券的期望收益率;m表示組合里有m種證券。
關於收益率的歷史數據可以表示為N種場景:
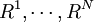 ,其中
,其中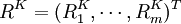 ,指歷史數據中第K時期末組合的收益率場景,而R^K_i指歷蟲數據中K時期末組合中第t種證券的收益率,這裡有兩點必須說明:①這些場景是由歷史數據構成或者由某一概率函數得來的,對問題的說明並不重要,因為數據的由來並不對以下計算造成影響②為了簡單起見,賦予每個場景以相同的權重.實際中,因為較遠的歷史數據對組合的未米預期影響較小,所以比較遠的場景賦予較小的權重,如果要採用不同的權重,下麵的計算方法依然有效。
,指歷史數據中第K時期末組合的收益率場景,而R^K_i指歷蟲數據中K時期末組合中第t種證券的收益率,這裡有兩點必須說明:①這些場景是由歷史數據構成或者由某一概率函數得來的,對問題的說明並不重要,因為數據的由來並不對以下計算造成影響②為了簡單起見,賦予每個場景以相同的權重.實際中,因為較遠的歷史數據對組合的未米預期影響較小,所以比較遠的場景賦予較小的權重,如果要採用不同的權重,下麵的計算方法依然有效。
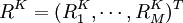 ,
,
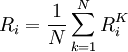 ,
,
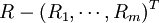 ,
,
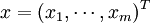
這樣,證券組合x的期望收益為:
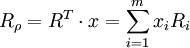
對於場景RK證券組合的收益率為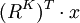 ,一個固定的場景收益率與期望收益之差可表示為
,一個固定的場景收益率與期望收益之差可表示為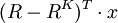 。因此,對具體的場景VaR值小於等於V可表示為:
。因此,對具體的場景VaR值小於等於V可表示為:
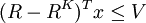
取時間跨度為一周時,收益率指周收益率,置信度c=95%時,則所有場景中的95%都應滿足上述條件。
令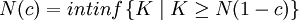 ,
,
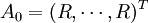 ,
,
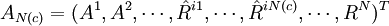 ,
,
式中: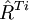 表示不考慮此場景,j=1,…,N(c),因此,給定一個VaR值,要求確定收益最大的證券組合可描述為以下模型。
表示不考慮此場景,j=1,…,N(c),因此,給定一個VaR值,要求確定收益最大的證券組合可描述為以下模型。
模型:尋找使期望收益RTx達到最大的投資組合x,它描述VaR約束條件與財富約束條件:
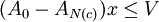 ,
,
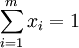 ,
,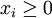
- ↑ 文鳳華 楊曉光 馬超群 巢劍雄 蘭秋軍.基於風險價值的投資決策分析.湖南大學學報(自然科學報).2005年12月第32捲第6期