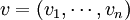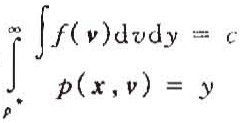投资决策分析
出自 MBA智库百科(https://wiki.mbalib.com/)
投资决策分析(investment decision analysis)
目录 |
投资决策分析是对各种建设投资方案进行综合分析。投资是为一定目的而预先垫付资金或实物的行为,又称为固定资产投资。
投资决策分析包括投资规模决策分析、投资方向决策分析和工程项目投资决策分析。前两者属于宏观经济范畴,后者属于微观经济范畴。
(1)投资规模决策分析
社会的发展要求尽可能多地进行固定资产投资。但投资的供给能力受很多因素的制约,主要取决于国民收入的数量及其增长速度,积累基金和消费基金的分配比例,固定资产积累、流动资产积累和社会后备基金的分配比例,固定资产折旧率等。投资规模的决策分析就是以经济发展战略为指导,研究投资的供给能力,从而确定固定资产投资的数量、增长速度和战线的长短。投资是一个较长的过程,在一定期间内要支出大量的劳动力和生产资料而不提供任何有效用的产品或服务,所以必须通过决策分析来确定固定资产投资的合理规模,以保证国民经济的综合平衡,人民生活的不断改善和生产的正常进行,同时也为了保证固定资产投资的经济效益。
(2)投资方向决策分析
投资方向决策分析就是以经济发展战略为指导,根据国民经济有计划按比例发展的客观要求,确定固定资产投资在国民经济各部门、各地区之间的分配比例。由于投资的分配比例决定着固定资产再生产的比例,从而在很大程度上决定着国民经济产业结构、工业部门结构和工业布局的合理性,所以投资方向的决策分析也是保证国民经济综合平衡和固定资产投资经济效益的重要环节。
(3)工程项目投资决策分析
指对于待选工程项目及其各种投资方案进行评价比较,依据项目的可行性和预期的社会经济效果而决定取舍的选择过程。各国进行投资决策分析的经济依据是不一样的。在苏联,由国家颁布基本建设投资经济效果的标准计算方法。在西方,生产性项目一般由私人投资,采用财务报表分析法、偿还期法和目前被认为是最有效的现金流量贴现方法进行企业财务评价;非生产性的公共工程项目一般由政府投资、评价方法采用成本效益分析或多目标决策。在发展中国家,由于价格失真、政府对私人投资的干预较多等原因,所以广泛采用基于成本效益分析的各种评价方法。中国近年来引入的工程项目可行性研究方法中,作为投资决策主要依据的国民经济评价方法就是一种成本效益分析方法。
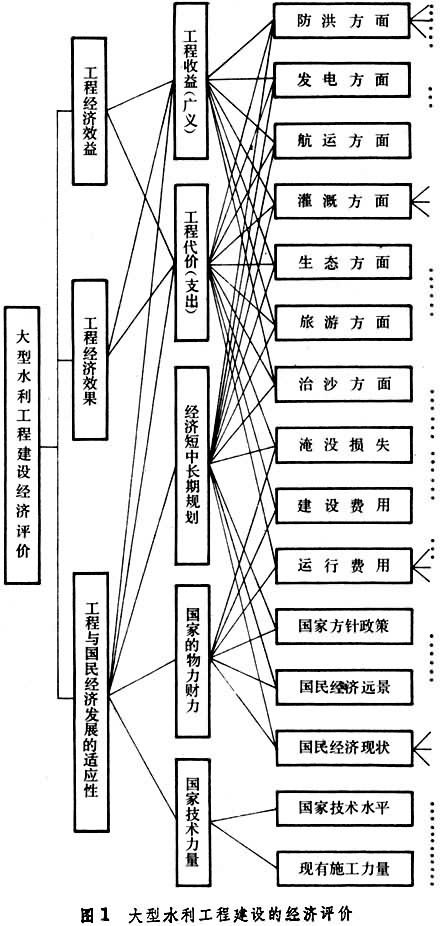
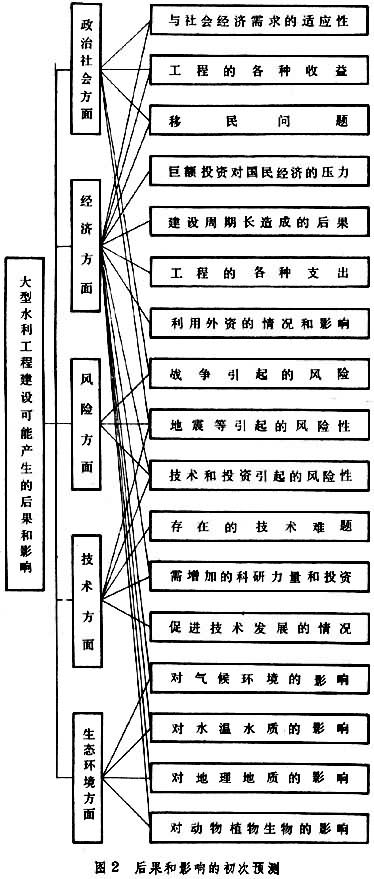
任何工程项目都是一个复杂的大系统,应用系统工程的方法时,首先要从系统整体出发,进行总体效益的分析。例如,对大型水利工程项目进行投资决策分析时,可能涉及防洪、发电、航运、灌溉、水产、旅游、治沙、防碱、治涝等方面,要从政治、社会、经济、技术和生态环境诸方面进行综合评价(图 1)。对于复杂的大型工程项目,不仅要弄清楚有哪些因素影响工程建设,而且要研究工程建设将会产生哪些后果和影响(图 2),然后对工程方案进行综合评价。最后要研究出一套决策方法,协助决策者在综合评价的基础上作出抉择。为了解决大型工程建设的决策问题,一般是把定性分析与定量分析结合起来,为此要建立决策模型。
决策模型应满足以下几个方面的要求:
①能够同时接受定性的信息和定量的信息,主观的信息和客观的信息;
②尽可能降低对指标评价精度的要求,以适应社会经济系统的实际情况;
③适应于离散方案集的情况;
④便于集中多种不同的决策观点,将个体决策与群决策结合起来。一般可采用目标规划法、组合规划法、多指标人机对话选优法等方法来建立决策模型。
投资决策分析的案例分析[1]
Markowitz证券组合理论的核心在于,选择风险最小、收益最大的证券组合,其中收益用均值描述,而风险用方差描述由于越来越多的金融机构采用vaR测量市场风险,使用vaR作为风险限额,特别是监管当局也在使用vaR确定风险资本金,因此许多金融机构及其业务部门在做投资选择时,往往需要满足VaR约束.即给定一个VaR.要求确定收益最大的证券组合,并同时满足vaR约束;或在市场条件变化情况下,在给定的vaR范围内,获得一个最优投资重组(重新平衡)策略,使得投资组合收益最大。
1.基于风险价值投资决策问题分析
首先给出相关变量的定义和说明.考虑由n种资产构成的资产集合,这些资产可以是股票、债券、期权等金融资产一个投资组合J由其在这些资产中的头寸决定:
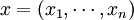
投资组合x在给定风险因子v下的价值为p(x,v),它是关于x和v的一个复杂非线性函数(甚至是不连续的)实际中p(x,v)可以表示为:
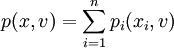
当组合中的资产都是股票时,可以简化为头寸与风险因子的线性组合形式:
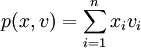
用v0表示t=0时风险因子的价值,t=1时风险因子的行为可由概率密度函数为f(v)的分布描述,则在t=l时的投资组合的价值均由概率密度函数为尹 的分布表示:
的分布表示:
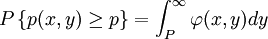
用风险因子的概率密度函数f(v)和投资组合的价值函数p(x,y)表示,就是:
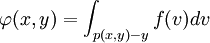
在实际中寻找这一分布函数极为困难,特别是当投资组合包含数以百计的资产或p(x,y)为非线性形式时但研究关于该分布函数的逼近过程的文献还是比较多。
现在给出投资组合x的VaR,用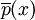 表示t=1时刻投资组合的期望价值:
表示t=1时刻投资组合的期望价值:
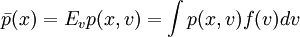
选择置信水平c,p * 示组合的最小价值:
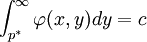 ,
,
则由相对vaR定义:
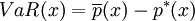
考虑投资组合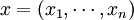 ,其中xi是第i种资产的投资权重,
,其中xi是第i种资产的投资权重,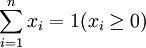 ,在这种情况下,需要解决的是下述问题:。
,在这种情况下,需要解决的是下述问题:。
问题:寻找使vaR
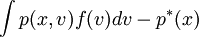
达到最小的投资组合x,它满足下列条件:
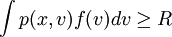 ,
,
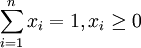
问题求解的典型算法是梯度法。当p(x,v)关于(x,v)可微,梯度px(x,v)和pv(x,v)满足Lipshitz条件,且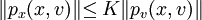 时,有
时,有
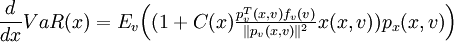
式中: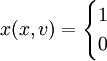 如果
如果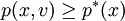 ,否则,
,否则,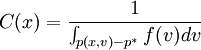
因此,VaR的梯度计算涉及3个变量的估计,即
p * (x)积分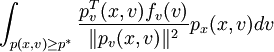 和
和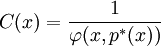 其中
其中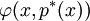 是投资组合的价值分布函数在y = p * (x)处的密度,它可以在计算VaR时自然求得。
是投资组合的价值分布函数在y = p * (x)处的密度,它可以在计算VaR时自然求得。
2.基于历史风险价值的投资决策模型
我们考虑资产组合里所有金融资产为股票的情况,此时证券组合的收益率与组合的权重x成线性关系:。
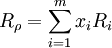 式中:Rρ为证券组合的收益率;Ri为第i种证券的期望收益率;m表示组合里有m种证券。
式中:Rρ为证券组合的收益率;Ri为第i种证券的期望收益率;m表示组合里有m种证券。
关于收益率的历史数据可以表示为N种场景:
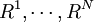 ,其中
,其中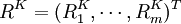 ,指历史数据中第K时期末组合的收益率场景,而R^K_i指历虫数据中K时期末组合中第t种证券的收益率,这里有两点必须说明:①这些场景是由历史数据构成或者由某一概率函数得来的,对问题的说明并不重要,因为数据的由来并不对以下计算造成影响②为了简单起见,赋予每个场景以相同的权重.实际中,因为较远的历史数据对组合的未米预期影响较小,所以比较远的场景赋予较小的权重,如果要采用不同的权重,下面的计算方法依然有效。
,指历史数据中第K时期末组合的收益率场景,而R^K_i指历虫数据中K时期末组合中第t种证券的收益率,这里有两点必须说明:①这些场景是由历史数据构成或者由某一概率函数得来的,对问题的说明并不重要,因为数据的由来并不对以下计算造成影响②为了简单起见,赋予每个场景以相同的权重.实际中,因为较远的历史数据对组合的未米预期影响较小,所以比较远的场景赋予较小的权重,如果要采用不同的权重,下面的计算方法依然有效。
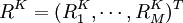 ,
,
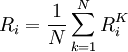 ,
,
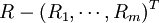 ,
,
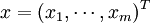
这样,证券组合x的期望收益为:
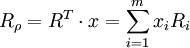
对于场景RK证券组合的收益率为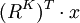 ,一个固定的场景收益率与期望收益之差可表示为
,一个固定的场景收益率与期望收益之差可表示为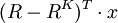 。因此,对具体的场景VaR值小于等于V可表示为:
。因此,对具体的场景VaR值小于等于V可表示为:
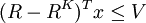
取时间跨度为一周时,收益率指周收益率,置信度c=95%时,则所有场景中的95%都应满足上述条件。
令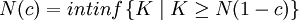 ,
,
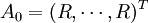 ,
,
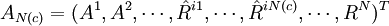 ,
,
式中: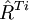 表示不考虑此场景,j=1,…,N(c),因此,给定一个VaR值,要求确定收益最大的证券组合可描述为以下模型。
表示不考虑此场景,j=1,…,N(c),因此,给定一个VaR值,要求确定收益最大的证券组合可描述为以下模型。
模型:寻找使期望收益RTx达到最大的投资组合x,它描述VaR约束条件与财富约束条件:
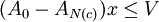 ,
,
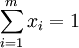 ,
,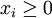
- ↑ 文凤华 杨晓光 马超群 巢剑雄 兰秋军.基于风险价值的投资决策分析.湖南大学学报(自然科学报).2005年12月第32卷第6期