中心極限定理
出自 MBA智库百科(https://wiki.mbalib.com/)
中心極限定理(Central Limit Theorems)
目錄 |
大數定律揭示了大量隨機變數的平均結果,但沒有涉及到隨機變數的分佈的問題。而中心極限定理說明的是在一定條件下,大量獨立隨機變數的平均數是以正態分佈為極限的。
中心極限定理是概率論中最著名的結果之一。它提出,大量的獨立隨機變數之和具有近似於正態的分佈。因此,它不僅提供了計算獨立隨機變數之和的近似概率的簡單方法,而且有助於解釋為什麼有很多自然群體的經驗頻率呈現出鐘形(即正態)曲線這一事實,因此中心極限定理這個結論使正態分佈在數理統計中具有很重要的地位,也使正態分佈有了廣泛的應用。
中心極限定理也有若幹個表現形式,這裡僅介紹其中四個常用定理:
(一)辛欽中心極限定理
設隨機變數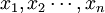 相互獨立,服從同一分佈且有有限的數學期望a和方差σ2,則隨機變數
相互獨立,服從同一分佈且有有限的數學期望a和方差σ2,則隨機變數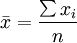 ,在n無限增大時,服從參數為a和
,在n無限增大時,服從參數為a和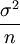 的正態分佈即n→∞時,
的正態分佈即n→∞時,
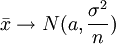
將該定理應用到抽樣調查,就有這樣一個結論:如果抽樣總體的數學期望a和方差σ2是有限的,無論總體服從什麼分佈,從中抽取容量為n的樣本時,只要n足夠大,其樣本平均數的分佈就趨於數學期望為a,方差為σ2 / n的正態分佈。
(二)德莫佛——拉普拉斯中心極限定理
設μn是n次獨立試驗中事件A發生的次數,事件A在每次試驗中發生的概率為P,則當n無限大時,頻率設μn / n趨於服從參數為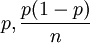 的正態分佈。即:
的正態分佈。即:
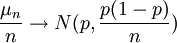
該定理是辛欽中心極限定理的特例。在抽樣調查中,不論總體服從什麼分佈,只要n充分大,那麼頻率就近似服從正態分佈。
(三)李亞普洛夫中心極限定理
設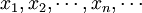 是一個相互獨立的隨機變數序列,它們具有有限的數學期望和方差:
是一個相互獨立的隨機變數序列,它們具有有限的數學期望和方差: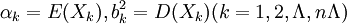 。
。
記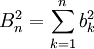 ,如果能選擇這一個正數δ>0,使當n→∞時,
,如果能選擇這一個正數δ>0,使當n→∞時,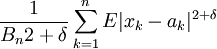 ,則對任意的x有:
,則對任意的x有:
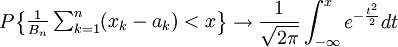
該定理的含義是:如果一個量是由大量相互獨立的隨機因素影響所造成的,而每一個別因素在總影響中所起的作用不很大,則這個量服從或近似服從正態分佈。
(四)林德貝爾格定理
設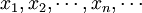 是一個相對獨立的隨機變數序列,它們具有有限的數學期望和方差 滿足林德貝爾格條件,則當n→∞時,對任意的x,有
是一個相對獨立的隨機變數序列,它們具有有限的數學期望和方差 滿足林德貝爾格條件,則當n→∞時,對任意的x,有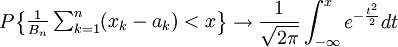 。
。
案例一:中心極限定理在商業管理中的應用[1]
水房擁擠問題:假設西安郵電學院新校區有學生5000人,只有一個開水房,由於每天傍晚打開水的人較多,經常出現同學排長隊的現象,為此校學生會特向後勤集團提議增設水龍頭。假設後勤集團經過調查,發現每個學生在傍晚一般有1%的時間要占用一個水龍頭,現有水龍頭45個,現在總務處遇到的問題是:
(1)未新裝水龍頭前,擁擠的概率是多少?
(2)至少要裝多少個水龍頭,才能以95%以上的概率保證不擁擠?
解:(1)設同一時刻,5000個學生中占用水龍頭的人數為X,則
X~B(5000,0.01)
擁擠的概率是
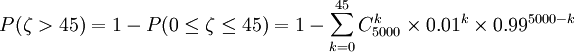
有定理2,n=5000,p=0.01,q=0.99,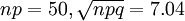
故

即擁擠的概率
P(ζ > 45) = 1 − 0.2389 = 0.7611
(2)欲求m,使得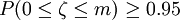
即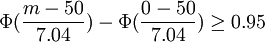
由於
即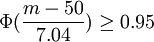
查表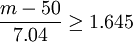
即
需裝62個水龍頭。
問題的變形:
(3)至少安裝多少個水龍頭,才能以99%以上的概率保證不擁擠?
解:欲求m,使得
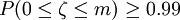
即
由
即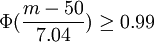
查表
即m≥66.4
故需要裝67個水龍頭。
(4)若條件中已有水龍頭數量改為55個,其餘的條件不變,1,2兩問題結果如何?
解:(1)

(2)同上。
(5)若條件中的每個學生占用由1%提高到1.5%,其餘的條件不變,則(1),
(2)兩問題結果如何?
解:(1)設同一時刻,5000個學生中占用水龍頭的人數為X,則
X-B(5000,0.015)
已知n=5000,p=0.015,q=0.985,np=75,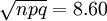
擁擠的概率達

(2)欲求m,使得
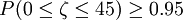
即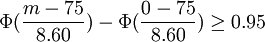
由
即
查表
即m≥89.14
故需裝90個水龍頭。
中心極限定理以嚴格的數學形式闡明瞭在大樣本條件下,不論總體的分佈如何,樣本的均值總是近似地服從正態分佈。如果一個隨機變數能夠分解為獨立同分佈的隨機變數序列之和,則可以直接利用中心極限定理進行解決。總之,恰當地使用中心極限定理解決實際問題有著極其重要意義。
- ↑ 孔祥鳳.中心極限定理在管理中的應用[J].現代商業,2009,(4).
評論(共20條)
比百度好,
肯定比百度好,百度上不過是些阿貓阿狗隨處找來的信息
不錯,如果能夠附加應用例子就更好了
添加了案例,希望對您有幫助!
參考文獻在第幾頁????
您好,參考文獻中的是一篇論文,希望對您有幫助!
爛,很多編輯錯誤,搞得我一時都看不懂了
您好,您能否指出哪些編輯錯誤呢?
MBA智庫百科是可以自由參與的百科,如有發現錯誤和不足,您也可以參與修改編輯,只要通過網頁右上角的創建新帳號,創建用戶名後即可參與,期待您的加入!~
normal approximate binomial distribution centered at n*p with variance n*p*q,rather than p, pq/n
有定理2,n=5000,p=0.01,q=0.985,np=50,\sqrt{npq}=7.04, 這行中“q”應為0.99,寫錯了
有定理2,n=5000,p=0.01,q=0.985,np=50,\sqrt{npq}=7.04, 這行中“q”應為0.99,寫錯了
謝謝指正,已修改!
MBA智庫百科是可以自由參與的百科,如有發現錯誤和不足,您也可以參與修改編輯,點擊條目上方的編輯進入即可參與,期待您的加入!~








我找你好久了,,,,,,,,,,,,,,,,好!