信用組合觀點模型

出自 MBA智库百科(https://wiki.mbalib.com/)

信用組合觀點模型(Credit Portfolio View，CPV)

目錄 1 什麼是信用組合觀點模型[1] 2 信用組合觀點模型的基本原理及框架[2] 3 信用組合觀點模型的優缺點[3] 4 CPV模型與其他信用風險量化模型比較[4] 5 相關條目 6 參考文獻

　　信用組合觀點模型是由麥肯錫公司應用計量經濟學理論和蒙特·卡羅模擬法於1998年開發出的一個多因素信用風險量化模型，它主要用於信貸組合風險的分析。

　　信用組合觀點(Credit Portfolio View)模型是由麥肯錫(Mckinsey)開發的一個多因數模型，可以用於模擬既定巨集觀因素取值下各個信用等級對象之間聯合條件違約分佈和信用轉移概率。在觀測到失業率、GDP增長率、長期利率水平、外匯水平、政府支出和國民儲蓄率等巨集觀經濟因數信息時，計算不同國家、不同行業、不同信用評級的違約和信用潛移概率的分佈函數。此模型假定每個債券的信用評級對整體的信用周期更敏感。

　　Credit Portfolio View將觀測到的違約概率和信用潛移概率與巨集觀經濟因素聯繫起來。當經濟處於衰退期時，各信用主體信用降級和違約概率增加；與此相反，當經濟處於繁榮時期時，各信用主體信用降級和違約概率減少。也就是說信用周期與經濟周期密切相關。假定能夠得到相關的數據，這一框架可以應用到每一個國家，並可用到像製造業、金融業和農業等不同的部門和各種類型的信用個體。

　　1．違約預測模型

　　違約概率為一個Logit函數，其變數為一些巨集觀經濟變數的當前值或滯後值構造的綜合評級指數，可表示為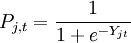：　　(1)

　　其中，P_j,t表示國家或行業j中債券在時期t的條件違約概率，Y_j,t表示由巨集觀經濟變數構造的評級指數。註意上述Logit變換保證了計算得到的違約概率處於0與1之間。

　　某一時期一個國家經濟狀況的巨集觀經濟指數Y_j,t可用下述的多因數模型來表示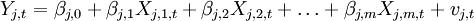：　　(2)

　　其中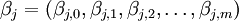，為第j個國家、產業或級別的參數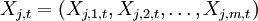；為時期t第j個國家或行業的巨集觀經濟變數；v_j,t表示與巨集觀經濟向量X_j,t獨立的殘差變數，並假設服從正態分佈：v_j,t—N(O,σ_j)，和v_t—N(O,∑_v)，這裡，v_t表示殘差變數v_j,t的向量形式，∑_v表示j×j的方差協方差矩陣。

　　對每一個國家來說，巨集觀經濟變數都是給定的。如果能夠得到足夠的數據，上述模型就可以在國家或產業的水平上進行計算，從而就可以估計出相應的違約概率P_j,t、違約概率指數Y_j,t和相應的參數β_j。

　　實際估計時，一般假設巨集觀經濟變數服從2階自回歸(AR2)過程：X_j,i,t = r_j,i,0 + r_j,i,1X_{j,i,t − 1} + r_j,i,2X_{j,i,t − 2} + e_j,i,t　　(3)

　　其中，X_{j,i,t − 1}，r_j,i,2X_{j,i,t − 2}表示巨集觀經濟變數X_j,t的一階和二階的滯後項；r_j = (r_j,i,0,r_j,i,1,r_j,i,2)表示需要估計的參數；e_j,i,t表示獨立同分佈的殘差項；e_j,i,t-N(O，σ_ej,i,t)和e_t-N(O，∑_e)。其中，e_t表示殘差e_j,i,t的向量形式，∑_e為(j×i)(j×i)的方差協方差矩陣。

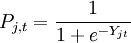
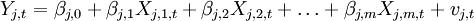
　　為了計算違約概率，需要考慮下麵的幾個方程(4)：X_j,i,t = r_j,i,0 + r_j,i,1X_{j,i,t − 1} + r_j,i,2X_{j,i,t − 2} + e_j,i,t

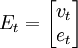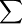　　其中殘差的向量E_t表示為-N(O，)，這裡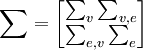,∑_v,e和∑_e,v表示交叉的協方差陣。

　　在計算了(4)的幾個方程後，可以通過以下步驟來計算違約概率：

　　第一步：對協方差矩陣∑進行Cholesky分解，即：∑=AA’　　(5)

　　第二步：產生標準正態分佈的隨機向量Z_t-N(0，I)，然後計算E_t=A’Z_t，所得的結果就是v_j,t和e_j,i,t，代入(4)的估計值就得到了Y_j,t和P_j,t。

　　2．條件轉移矩陣

　　為了推導條件信用轉移矩陣，我們使用根據穆迪(Moody)公司或標準普爾(Standard & Poor)公司的歷史數據計算的信用等級轉移矩陣(無條件的馬爾可夫轉移矩陣)，記做幣M。之所以稱為無條件轉移概率，因為它們是基於20年、跨越好幾個經濟周期和產業的數據之上推導的歷史平均數。

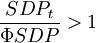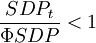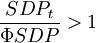　　非投資級的債務人在經濟衰退時期的違約概率平均較高，此時信用降級的概率下降，信用升級的概率上升，在經濟擴張時期，與此相反，即(6)：　　經濟衰退時　　經濟繁榮時 　　其中，SDP_t表示某級別債券的條件違約概率，ΦSDP表示某級別債券的無條件違約概率。Credit Portfolio View利用(6)調整非條件違約概率矩陣得到以經濟狀態為條件的信用轉移矩陣：M_t = M(P_j,t / ΦSDP)　　(7) 　　當經濟衰退時，時，增加了債券信用降級和違約的概率；當經濟繁榮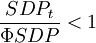，時，降低了債券信用降級和違約的概率。因為可以計算出任何經濟時期的轉移概率矩陣，那麼也就可以得到多期的轉移矩陣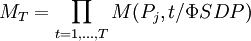：　　(8)

　　對上式模擬很多次，就能得到任何時期，任何評級的條件違約概率的分佈。

　　KMV和Credit Portfolio View都假設違約和轉移概率是隨時間變化的。KMV模型是利用微觀經濟的方法將債券的違約概率和資產的市場價值結合起來。Credit Portfolio View則是利用巨集觀經濟的框架將巨集觀經濟因數和違約概率、信用轉移概率結合起來，它需要每一個國家每一個部門的某些數據。上述模型的一個缺點是對於轉移概率的調整帶有一定的任意性。上述兩種方法也有一定的聯繫，因為公司資產的價值依賴於經濟的狀況。

　　信用組合觀點模型主要適用於投機級債務人，而不太適合於投資級債務人。因為投資級債務人的違約率相對穩定，而投機級債務人的違約率會受周期性巨集觀經濟因素的影響而劇烈變動，所以要根據巨集觀經濟狀況適時調整違約概率及其對應的信用等級轉移矩陣。

　　信用組合觀點模型將巨集觀經濟狀況納入模型中，用於模擬信用事件的信用風險，其優點是顯而易見的。但同時，該模型也存在著一些局限性。

　　(1)該法要求每個國家、甚至每個國家內的每個產業部門都要有完備可靠的違約數據，這顯然是很難實現，退一步來說，即使能夠實現，但如果模型中所包含的行業越多，關於違約事件的信息就會相對變得越少，這也將不利於條件違約概率的確定，並影響模型的應用效果。

　　(2)模型沒有考慮諸如債務的剩餘期限及其對債務償還情況等微觀經濟因素的影響，而是完全依賴巨集觀經濟因素來決定信用等級轉移概率，這有點過於武斷和片面。

　　(3)模型對企業信用等級變化所進行的調整，容易受銀行在信貸方面積累的經驗和對信貸周期的主觀認識等人為因素的影響，從而有可能降低調整後模型的客觀性、可信性。

　　(4)模型有可能受到調整信用等級轉移矩陣的特定程式的限制，而且也無法判定在實踐中是否一定比簡單的貝葉斯模型表現更好。

　　1．現代信用風險內部度量模型

　　銀行內部信用風險度量的依據是對借款人和具體交易類型風險特征進行評估並以此確定銀行可能遭受的損失，進而估計經濟資本。

　　CreditMetrics^TM是銀行業最早使用並且對外公開的信用風險管理模型，是由J．P．摩根銀行(JPM)和一些合作機構1997年推出的信用度量術。基礎是資產組合理論，旨在使信用按市值定價。著眼於流動性非常好的債券市場或債券衍生品市場，因此可以輕易收集廣泛的價格和評級數據。它對貸款和債券在給定的時間單位內(通常為1年)的未來價值變化分佈進行估計，並通過在險價值(Value at Risk，VaR)來衡量風險。這裡VaR用來衡量投資組合風險敞口的程度，是指在正常的市場情況和一定的置信水平下，在給定的時間段內預期可能發生的最大損失。

　　KMV是美國一家開發和出售信用分析軟體以及其他金融信息產品的專業公司，模型因公司而得名。KMV模型的理論基礎是Black-Scholes，Merton以及Hull和White的期權定價理論。該模型認為信用風險產生的動因是發行者的資產價值的變化。

　　從期權與公司資產價值的角度來看，公司的股東持有一份以公司債務為執行價格，以公司資產為標的物的看漲期權。當資產大於負債時，股東則行使該看漲期權，即償還債務，繼續擁有公司；如果資產小於負債，公司破產，公司所有者將公司資產出售給債權的持有人，即債權人擁有公司。所以企業破產的概率由企業的資產和負債共同決定。Merton模型把杠桿企業中的股權看作是一個以企業資產為標的，總負債賬麵價值為執行價格的看漲期權。如果貸款到期時企業市場價值高於其債務，企業有動力還款；當企業價值小於其債務時，企業有違約的選擇權。因此，企業的股權價值可以用Black-Scholes期權定價模型來定價。

　　CreditRisk ⁺ 是由瑞士信貸第一波士頓銀行(CSFB)於1996年在保險精算的基礎上開發的信貸風險管理系統。它假定違約率是隨機的，可以在信用周期內顯著地波動，並且其本身是風險的驅動因素馴。

　　因而，CreditRisk ⁺ 被認為是一種“違約率模型”的代表。與CreditMetrics^TM和KMV都以資產價值作為風險驅動因素不同，它只考慮了違約風險，而沒有對違約的成因做出任何假設：一個債務人或者以概率PA違約，或者以1一PA的概率沒有違約。它假定：(1)對於一筆貸款，在給定期間內的違約概率與其他任何期間的違約概率相同；(2)對於大量的債務人，任何特定債務人的違約概率很小，且在某一特定時期內的違約數與任何其他時期內的違約數相互獨立。

　　1998年McKinsey公司提出的CreditPonfolioView^TM模型(以下稱CPV模型)是一個用於分析貸款組合風險和收益的多因素模型，它根據諸如失業率、GDP增長率、長期利率水平、政府支出等巨集觀因素，運用經濟計量學和蒙特卡羅技術來對每個國家不同行業中不同等級的違約和轉移概率的聯合條件分佈進行模擬。與CreditMetrics^TM應用的轉移概率和違約率不同，CPV模型不是以歷史等級轉移和違約的數據來估計，而是以當期的經濟狀態為條件來計算債務人的等級轉移概率和違約率。模型中的違約概率和轉移概率都與巨集觀經濟狀況緊密相聯。當經濟狀況惡化時，降級和違約增加；反之，則減少。

　　2．現代信用風險度量模型的比較

　　CreditMetrics^TM，KMV，CreditRisk ⁺ 和CPV模型4種方法是當今國際上最具代表性的現代信用風險量化模型。它們建立的基礎和對風險評估的重點都有所不同，為了更好的進行分析，特從以下3個方面進行比較。

　　2．1信用損失的定義及驅動因素

　　根據模型對信用損失的不同定義，可以將模型分為兩類：以貸款的市場價值變化為基礎的模型稱為盯市模型(Mark-to-Market Model)，集中於預測違約損失的風險機制的模型稱為違約模型(Default Model)。盯市模型在計算貸款價值的損失和收益中既考慮了違約因素，同時也考慮了貸款信用等級上升或者下降以及由此發生的信用價差變化等因素。違約模型只考慮兩種狀態，即違約或者不違約。盯市模型和違約模型之間的關鍵差異是盯市模型包括了價差風險。在以上的4個模型中，KMV模型和CreditMetrics^TM模型明顯是盯市模型，CreditRisk ⁺ 模型則是違約模型，而CPV模型既可以當作盯市模型也可以當作違約模型。

　　這些模型的關鍵風險驅動因素似乎不大相同，CreditMetrics^TM模型和KMV模型是以MeHon模型為分析基礎，企業的資產價值和資產價值的波動性是違約風險的關鍵性驅動因素。在CPV模型觀點中，信用風險驅動因素是一些巨集觀因素。在CreditRisk ⁺ 模型中，信用風險的驅動因素則是違約率及其波動性。然而，如果從多因素角度來考慮，4種模型都可以看作有著類似的根源。

　　CPV模型中風險驅動因素有著與CreditMetrics^TM模型和KMV模型在本質上的相似之處。特別是，一套系統的“國家範圍的”巨集觀因素和非系統的巨集觀衝擊驅動著違約風險和借款人之間的違約風險的相關性。在CreditRisk ⁺ 模型中，關鍵的信用風險驅動因素是經濟中可變的違約率均值。違約率均值可以被看作是與巨集觀經濟狀態系統地聯繫在一起，一旦巨集觀經濟惡化，則違約率就可能上升，違約率波動性也一樣。經濟形式的改善則有著相反的效應。

　　2．2信用事件的可變性及相關性

　　在關於信用事件的可變性方面，各個模型之間的關鍵差異在於，是為違約率建立模型，還是為違約分佈函數的概率建立模型。在CreditMetrics^TM模型中，違約率和信用等級轉化概率被模型化為基於歷史數據的固定的或離散的值。在KMV模型中，預期違約率隨著新信息被納入股票價格而發生變化，股票價格變化以及股票價格的波動性稱為KMV模型中預期違約率計量的基礎。在CreditRisk ⁺ 模型中，每筆貸款違約率被看作是可變的，並且服從圍繞某些違約率均值的泊松分佈，因此，違約率均值被模型化為一個服從r分佈的變數。無論是與CreditMetrics^TM模型還是與CPV模型比較，由CreditRisk ⁺ 模型可以產生一種可能有“更厚實的尾部”的損失分佈。在CPV模型中，違約率是一套呈正態分佈的巨集觀因素和衝擊的對數函數，因此，隨著巨集觀經濟的演變，違約率以及信用等級轉換矩陣中概率也會變化。

　　在信用事件的相關性方面，各模型具有不同的相關性結構，KMV模型和CreditMetrics^TM是多變數正態；CPV模型是因素負載；而CreditRisk ⁺ 模型是獨立假定或與預期違約率的相關性。

　　2．3信用風險因數的計算方法

　　CreditMetrics^TM模型考慮可以讓貸款違約損失利發生變化，在該模型為正態分佈的情況下，估計的違約損失率的標準差被納入了VaR的計算，在“實際”分佈的情況下，考慮到貸款價值損失分佈函數尾部的偏斜，因而假定違約損失率服從β分佈，並且貸款的VaR通過蒙特卡羅模擬法來計算。

　　在KMV最簡單的模型中，違約損失率被看作是一個常數。在該模型最新的發展中，也允許回收率遵循β分佈。在CreditRisk ⁺ 模型中損失的嚴重程度被劃分區間並湊成整數，從而得到次級的貸款組合，然後將任何次級貸款組合的損失的嚴重程度視為一個常數。在CPV模型中，違約損失率的估計也是通過蒙特卡羅模擬法進行的。

表1 4種信用風險量化模型的比較

	CreditMetricsTM模型	KMV模型	CreditRisk + 模型	CreditPortifolioViewTM模型
信用損失定義	盯市方法	盯市方法或違約模式	違約模式	盯市方法或違約模式
風險驅動因素	資產價值	資產價值	期望違約率	巨集觀經濟因素
信用事件可變性	不變	可變	可變	可變
信用事件的相關性	多變數正態資產收益	多變數正態資產收益	獨立假設或期望違約率相關	隨因素變化
違約回收率	隨機	常數或隨機	分區域，每一區域為一值	隨機
計算方法	模擬或分析	分析	分析	模擬

　　4個模型在估計VaR和預期損失的計算方法上是不盡相同的。不論是在個別貸款的層次上，還是在貸款組合的層次上，CreditMetrics^TM模型均可以將組合的VaR有邏輯地分析和計量出來。但是隨著貸款組合中貸款數目的增加，這一方法會變得越來越難以處理。結果是，對於大額的組合貸款組合CreditMetrics^TM模型需要運用蒙特卡羅模擬技術來產生一個組合貸款價值的“近似的”總體分佈，並由此計算出VaR。類似地，CPV模型中使用重覆的蒙特卡羅模擬法來生成巨集觀衝擊和貸款組合損失或貸款價值的分佈，從而最終也能算出VaR。向比較而言，CreditRisk ⁺ 模型基於其方便的假定(個別貸款呈泊松分佈，違約率均值呈r分佈，以及假定在貸款組合中貸款損失有固定的回收率)，能夠生成關於損失的概率密度函數的邏輯分析解或閉型解。另外，KMV模型也可以獲得損失函數的邏輯分析解。

• KMV模型
• 信用度量制模型
• 信用風險附加計量模型