Creditmetrics模型
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
Creditmetrics模型(信用計量模型)是J.P.摩根在1997年推出的用於量化信用風險的風險管理產品。與1994年推出的量化市場風險的Riskmetrics一樣,該模型引起了金融機構和監管當局的高度重視,是當今風險管理領域在信用風險量化管理方面邁出的重要一步。
1、信用風險取決於債務人的信用狀況,而企業的信用狀況由被評定的信用等示。因此,信用計量模型認為信用風險可以說直接源自企業信用等級的變化,並假定信用評級體系是有效的,即企業投資失敗、利潤下降、融資渠道枯竭等信用事件對其還款履約能力的影響都能及時恰當地通過其信用等級的變化而表現出來。信用計量模型的基本方法就是信用等級變化分析。轉換矩陣(Transition Matrix一般由信用評級公司提供),即所有不同信用等級的信用工具在一定期限內變化(轉換)到其他信用等級或維持原級別的概率矩陣,成為該模型重要的輸入數據。
2、信用工具(包括債券和貸款等)的市場價值取決於債務發行企業的信用等級,即不同信用等級的信用工具有不同的市場價值,因此,信用等級的變化會帶來信用工具價值的相應變化。根據轉換矩陣所提供的信用工具信用等級變化的概率分佈,同時根據不同信用等級下給定的貼現率就可以計算出該信用工具在各信用等級上的市場價值(價格),從而得到該信用工具市場價值在不同信用風險狀態下的概率分佈。這樣就達到了用傳統的期望和標準差來衡量資產信用風險的目的,也可以在確定的置信水平上找到該信用資產的信用值,從而將Var的方法引入到信用風險管理中來。
3、信用計量模型的一個基本特點就是從資產組合而並不是單一資產的角度來看待信用風險。根據馬柯威茨資產組合管理理論,多樣化的組合投資具有降低非系統性風險的作用,信用風險很大程度上是一種非系統性風險,因此,在很大程度上能被多樣性的組合投資所降低。另一方面,由於經濟體系中共同的因素(系統性因素)的作用,不同信用工具的信用狀況之間存在相互聯繫,由此而產生的系統性風險是不能被分散掉的。這種相互聯繫由其市場價值變化的相關係數(這種相關係數矩陣一般也由信用評級公司提供)表示。由單一的信用工具市場價值的概率分佈推導出整個投資組合的市場價值的概率分佈可以採取馬柯威茨資產組合管理分析法。
4、由於信用計量模型將單一的信用工具放入資產組合中衡量其對整個組合風險狀況的作用,而不是孤立地衡量某一信用工具自身的風險,因而,該模型使用了信用工具邊際風險貢獻這樣的概念來反映單一信用工具對整個組合風險狀況的作用。邊際風險貢獻是指在組合中因增加某一信用工具的一定持有量而增加的整個組合的風險(以組合的標準差表示)。通過對比組合中各信用工具的邊際風險貢獻,進而分析每種信用工具的信用等級、與其他資產的相關係數以及其風險暴露程度等各方面因素,可以很清楚地看出各種信用工具在整個組合的信用風險中的作用,最終為投資者的信貸決策提供科學的量化依據。
(一) 在險價值(VaR)方法:
在險價值模型就是為了度量一項給定的資產或負債在一定時間里和在一定的置信度下其價值最大的損失額。
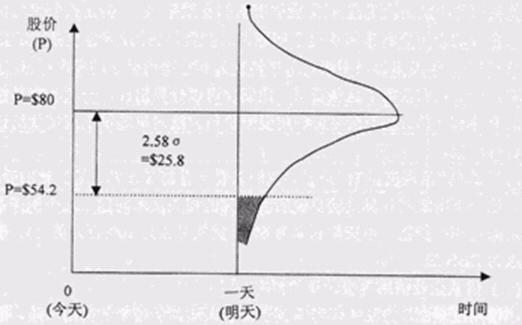
一支交易股票的在險價值
VaR方法度量非交易性金融資產如貸款的在險價值時則會遇到如下問題:
1.因為絕大多數貸款不能直接交易,所以市值P不能夠直接觀察到。
2.由於貸款的市值不能夠觀察,也就無法計算貸款市值的變動率σ。
3.貸款的價值分佈離正態分佈狀偏差較大。
(二)“信用度量制”方法(CreditMetrics)
信用度量制是通過掌握借款企業的資料如:
(1)借款人的信用等級資料
(2)下一年度該信用級別水平轉換為其它信用級別的概率
(3)違約貸款的收復率
計算出非交易性的貸款和債券的市值P和市值變動率σ,從而利用在險價值方法對單筆貸款或貸款組合的在險價值量進行度量的方法。
Creditmetrics模型與KMV模型的比較
KMV模型與creditmetrics模型是目前國際金融界最流行的兩個信用風險管理模型。兩者都為銀行和其它金融機構在進行貸款等授信業務時衡量授信對象的信用狀況,分析所面臨的信用風險,防止集中授信,進而為實現投資分散化和具體的授信決策提供量化的、更加科學的依據,為以主觀性和藝術性為特征的傳統信用分析方法提供了很好的補償。然而,從上述的介紹和分析中,我們又可以明顯地看到這兩個模型在建模的基本思路上又相當大的差異,這些差異還主要表現在以下幾個方面。
1、KMV模型對企業信用風險的衡量指標edf主要來自於對該企業股票市場價格變化的有關數據的分析,而creditmetrics模型對企業信用風險的衡量來自於對該企業信用評級變化及其概率的歷史數據的分析。這是兩者最根本的區別之一。
2、由於KMV模型採用的是企業股票市場價格分析方法,這使得該模型可以隨時根據該企業股票市場價格的變化來更新模型的輸入數據,得出及時反映市場預期和企業信用狀況變化的新的edf值。因此,kmv模型被認為是一種動態模型,可以及時反映信用風險水平的變化。然而,creditmetrics採用的是企業信用評級指標分析法。企業信用評級,無論是內部評級還是外部評級,都不可能象股票市場價格一樣是動態變化的,而是在相當長的一段時間內保持靜態特征。這有可能使得該模型的分析結果不能及時反映企業信用狀況的變化。
3 、同時,也正是因為kmv模型所提供的edf指標來自於對股票市場價格實時行情的分析,而股票市場的實時行情不僅反映了該企業歷史的和當前的發展狀況,更重要的是反映了市場中的投資者對於該企業未來發展的綜合預期,所以,該模型被認為是一種向前看(forward-looking)的方法,edf指標中包含了市場投資者對該企業信用狀況未來發展趨勢的判斷。這與creditmetrics模型採用的主要依賴信用狀況變化的歷史數據的向後看(backward-looking)的方法有根本性的差別。kmv的這種向前看的分析方法在一定程度上剋服了依賴歷史數據向後看的數理統計模型的“歷來可以在未來複制其自身”的缺陷。
4 、KMV模型所提供的edf指標在本質上是一種對風險的基數衡量法,而creditmetrics所採用的與信用評級分析法則是一種序數衡量法,兩者完全不同。以基數法來衡量風險最大的特點在於不僅可以反映不同企業風險水平的高低順序,而且可以反映風險水平差異的程度,因而更加準確。這也更加有利於對貸款的定價。而序數衡量法只能反映企業間信用風險的高低順序,如bbb級高於bb級,卻不能明確說明高到什麼程度。
5、creditmetrics採用的是組合投資的分析方法,註重直接分析企業間信用狀況變化的相關關係,因而更加與現代組合投資管理理論相吻合。而kmv則是從單個授信企業在股票市場上的價格變化信息入手,著重分析該企業體現在股價變化信息中的自身信用狀況,對企業信用變化的相關性沒有給予足夠的分析。
案例一:基於CreditMetrics模型的商業銀行信用風險應用[1]
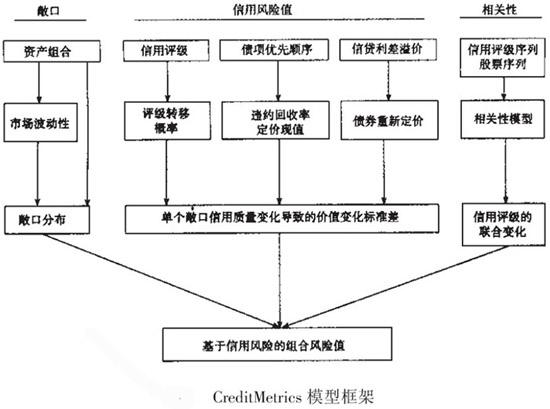
一、CreditMetrics模型的基本框架
對於CreditMetrics模型而言,影響信貸資產價值的因素即有違約事件,也有信貸資產質量的變化。為獲得所有信貸資產的潛在變化信息,CreditMetrics模型採取了盯市(Marked-to-Market)的方法來計算信用風險值。該模型構造了一個模擬信貸資產所有潛在變化以及違約波動的組合計量框架。圖2給出了模型的框架,從CreditMetrics模型技術框架看,該模型主要包括三個關鍵環節:
1.敞口或內部頭寸
頭寸數據通常都保存在金融機構一系列的系統當中,包括投資組合數據、交易賬簿數據以及表外項目數據等。只要頭寸數據的基礎是一致的,CreditMetrics就能區分出不同投資種類之間的風險差別。
2.信用事件所導致的單個敞口的價值波動
信用事件包括違約事件以及評級變動。在計算整個組合的信用風險之前,需要先計算單個頭寸的信用風險。計算的風險應能囊括信貸資產在所有各種可能的評級狀態下(包括違約)的價值分佈。
3.不同信貸資產彼此變化的相關性
CreditMetrics最終的目的是要計算整個信貸組合的信用風險,為此必須要估計不同資產之間的變化相關性,包括違約的相關性和評級轉移的相關性。
在估計組合的信貸資產風險值方面,相關性估計至關重要。
二、CreditMetrics模型信用度量方法
CreditMetrics模型度量是以信用評級轉移為基礎的,而信用評級並不只是由CreditMetrics集團提供的,可由用戶獨立開發,也可以從信用評級機構取得。典型的轉移計算是:在一年的時間內,以標準普爾的評級AAA、AA、A、BBB、BB、B和CCC為基礎,計算從一個評級轉移到另一個評級的轉移概率。除了以上7個信用評級外,還考慮表示“違約”的吸收狀況D,共計8種狀態。根據已知歷史數據估計的轉移概率,用公司的債券市場或股票市場數據替代公司資產價值直接導出評級分類的相關性,CreditMetrics計算貸款的組合的價值遠期分佈,直接估計一般信用損失分佈對應某個置信水平分位數作為資產信用風險值。
1.單一債券或貸款情況
CreditMetrics模型信用度量方法是以信用評級為基礎,通過求單項貸款價值概率分佈來確定單項貸款的風險。這個概率分佈的特點在於它完全基於信用轉移分析,即在既定時間內(一般取一年)一種信用質量變為另一種信用質量的概率,用它來度量將來(比如說一年以後)貸款資產組合的價值分佈,模型強調資產組合價值變化與信用評級轉移相關。假設一筆固定利率、不可提前償還的中長期貸款。該筆貸款是等額償還,直到最後一次償還時結清貸款本息。在不可提前償還假定條件下,根據普通年金現值一般公式,可推導出償還貸款額現值計算的基本模型:
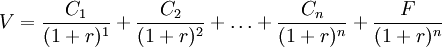
其中:V——債券價值;
C——每年的利息;
M——到期的本金;
r——貼現率(報酬率);
n——債券到期前的年數。
CreditMetrics模型的基礎是在給定的時間段內估計貸款或債券產品將來價值變化的分佈狀況,價值變化與債務人信用質量轉移(信用評級是上升,是下降,還是違約)相關。設信貸資產或債券價值6的均值為μ,方差為σ,則: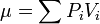
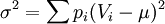
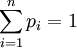
2.組合債券或貸款情況
(1)公司價值模型
下麵介紹信用計量模型所用的公司價值的基本原則——閾值方法。按照默頓模型,公司資產價值遵循標準幾何布朗運動,在時刻的公司價值服從對數正態分佈,並可表示為:
![V_t=V_0exp[(\mu-\frac{\sigma^2}{2}t+\sigma\sqrt{t}Z_t)]](/w/images/math/9/4/c/94c5a50b7d76d10c727a42e948e912c4.png)
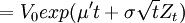
如果P_{Def}表示債務人違約概率,違約時資產價值為V_{Def},則有:
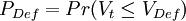 ……式中Zt − N(0,1),t時間預期限值服從對數分佈。
……式中Zt − N(0,1),t時間預期限值服從對數分佈。
E(Vt) = V0exp(ut)
當滿足以下條件時,違約就會發生:
![P_{Def}=Pr[\frac{ln\frac{V_{Def}}{V_0}-(\mu-\frac{\sigma^2}{2})}{\sigma\sqrt{t}}]\ge Z_t=Pr[Z_t\le\frac{ln\frac{V_{Def}}{V_0}+(\mu-\frac{\sigma^2}{2})}{\sigma\sqrt{t}}]=N(-d_2)](/w/images/math/8/a/6/8a691f946243ee107c8ff3263ee43db9.png)
其中N(g)是一個標準累積正態分佈,設d2為違約距離,則:
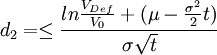
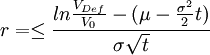
(2)聯合評級概率的推導
為了在聯合概率中考慮相關性,利用上面計算每筆貸款或新發行債券的閾值,再根據二元正態分佈計算出聯合概率。我們以初始評級為BBB和A級的公司為例,假設每個公司的資產價值正規化後對數收益rBBB和rA服從標準正態分佈,則聯合正態分佈的密度函數為:
![f(r_{BBB},r_A,\rho)=\frac{1}{2\pi\sqrt{1-\rho^2}}exp[\frac{-(r^2_A+r^2_{BBB}-2r_A r_{BBB})}{2(1-\rho^2)}]](/w/images/math/e/1/8/e1833854ad565e04a8e684ff29d91ef4.png)
為了推導每對資產最終評級的聯合概率,要完成下麵雙重積分計算:
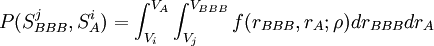 。
。
式中,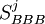 和
和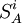 代表開始評級為BBB和A級公司的最終評級,分別為第/與第0級的狀態。
代表開始評級為BBB和A級公司的最終評級,分別為第/與第0級的狀態。
(3)聯合違約概率的推導
債務人1 和債務人2的違約事件分別為Def1和Def2,資產收益相關性是ρ,考慮兩個債務人違約概率分別為P_1(Def_1)和P_2(Def_2),則P1(Def1,Def2)是違約的聯合概率。假定資產收益率相關性ρ已知,表示為兩種資產標準化的對數收益服從聯合正態分佈,則
![f(r_{BBB},r_A;\rho)=\frac{1}{2\pi\sqrt{1-\rho^2}}exp[\frac{-1}{2(1-\rho^2)}(r^2_{BBB}-2\rho\gamma_{BBB}r_A+r^2_{BBB})]](/w/images/math/7/d/a/7da38c3f092ba3f6fa521dc71aa4d9a0.png)
違約相關性表示為
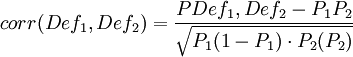
根據莫頓模型,兩個債務人違約的聯合概率是:
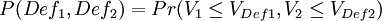
式中V_1和V_2為兩個債務人在時間的資產價值,7V_{Def1}是V_{Def2}引發違約的關鍵值。上式表達式等於:
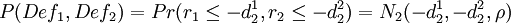
註:r1和r2表示債務人1和債務人2標準資產收益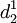 和
和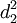 分別為違約距離,N2(x,y,ρ)表示兩變數的標準正態累積函數,ρ是x和y之間的相關係數。
分別為違約距離,N2(x,y,ρ)表示兩變數的標準正態累積函數,ρ是x和y之間的相關係數。
三、基於CreditMetrics模型的信貸資產風險值的計算實例
1.單一貸款或債券情況下的信用風險估值我們運用上述CreditMetrics模型方法計算單一情況下的信貸資產的風險值。下麵以一筆年利率為6%,金額為10000元,期限為5年,高級未擔保的BBB級不可提前償還的中長期貸款為例來計算CreditMetrics模型的信貸資產風險值。
第一步,確立轉移矩陣。轉移矩陣意味著一年內從一個信用等級轉變為另一個信用等級的概率,穆迪和標準普爾等級均有這樣的數據積累(見表1)。
表1 不同級別客戶一年期信用轉移矩陣(%)
| 始評級 | 年末評級 | |||||||
| AAA | AA | A | BBB | BB | B | CCC | 違約 | |
| AAA | 90.81 | 8.33 | 0.68 | 0.06 | 0.12 | 0.00 | 0.00 | 0.00 |
| AA | 0.70 | 90.65 | 7.79 | 0.64 | 0.06 | 0.14 | 0.02 | 0.00 |
| A | 0.09 | 2.27 | 91.05 | 5.52 | 0.74 | 0.26 | 0.01 | 0.06 |
| BBB | 0.02 | 0.33 | 5.95 | 86.93 | 5.30 | 1.17 | 0.12 | 0.18 |
| B+ | 0.03 | 0.14 | 0.67 | 7.73 | 80.53 | 8.84 | 1.00 | 1.06 |
| B | 0.00 | 0.11 | 0.24 | 0.43 | 6.48 | 83.46 | 4.07 | 5.20 |
| CCC | 0.22 | 0.00 | 0.22 | 1.30 | 2.38 | 11.24 | 64.86 | 19.79 |
與一年期轉移矩陣相對應,還有多年期累計平均違約率統計數據(見表2)
表2 不同級別客戶多年累計平均違約率(%)
| 期限 | 1 | 2 | 3 | 4 | 5 | 7 | 10 | 15 |
| AAA | 0.00 | 0.00 | 0.07 | 0.15 | 0.24 | 0.66 | 1.40 | 1.40 |
| AA | 0.00 | 0.02 | 0.12 | 0.25 | 0.43 | 0.89 | 1.29 | 1.48 |
| A | 0.06 | 0.16 | 0.27 | 0.44 | 0.67 | 1.12 | 2.17 | 3.00 |
| BBB | 0.18 | 0.44 | 0.72 | 1.27 | 1.78 | 2.99 | 4.34 | 4.70 |
| BB | 1.06 | 3.48 | 6.12 | 8.68 | 10.97 | 14.46 | 17.73 | 19.91 |
| B | 5.20 | 11.00 | 15.95 | 19.4 | 21.88 | 25.14 | 29.02 | 30.65 |
| CCC | 19.79 | 26.92 | 31.63 | 35.97 | 40.15 | 42.64 | 45.1 | 45.10 |
第二步,確立時間段。CreditMetrics模型中時間選取通常定為一年,這是出於會計數據和財務報告得到的頻率而定的。
第三步,確立遠期定價模型。信貸資產的估計可以從與貸款發行方評級對應的信貸資產得出。每個信用級別一年遠期零曲線見表3。
表3 每個信用等級的一年遠期零曲線(%)
| 範疇 | 一年 | 二年 | 三年 | 四年 |
| AAA | 3.6 | 4.17 | 4.73 | 5.12 |
| AA | 6.65 | 4.22 | 4.78 | 5.17 |
| A | 3.72 | 4.32 | 4.93 | 5.32 |
| BBB | 4.1 | 4.67 | 5.25 | 5.63 |
| BB | 5.55 | 6.02 | 6.78 | 7.27 |
| B | 6.05 | 7.02 | 8.03 | 8.52 |
| CCC | 15.03 | 15.05 | 14.03 | 13.52 |
如果一年後借款人仍是BBB級,一年後的信貸資產價格為:
 (元)。
(元)。
如果對每一級別重覆同樣計算,可以得到一年後不同級別貸款的價值,見表4。
表4 各信用級別的一年遠期價值
| 年末評級 | 價值 |
| AAA | 10935.29 |
| AA | 10917.24 |
| A | 10864.3 |
| BBB | 10753.09 |
| BB | 10200.64 |
| B | 9808.59 |
| CCC | 8362.34 |
| 違約 | 5113 |
第四步,得出將來組合價值變化的分佈。如果發生違約,根據優先償還程度,投資者可以得到部分清償,本例題中,高級末擔保貸款的清償率約為51.13%,10000元的清償額為5113美元。信貸資產質量變化產生的一年期的債券價值變化的分佈(見表5)。
表5 一年後該筆貸款的價值及變化
| 年末評級 | 評級變化的概率p(%) | 貸款價值(元) | 價值變化ΔV |
| AAA | 0.02 | 10935.29 | 182.2 |
| AA | 0.33 | 10917.24 | 164.15 |
| A | 5.95 | 10864.3 | 111.21 |
| BBB | 86.93 | 10753.09 | 0 |
| BB | 5.3 | 10200.64 | -552.45 |
| B | 1.17 | 9808.59 | -944.5 |
| CCC | 0.12 | 8362.34 | -2390.75 |
| 違約 | 0.18 | 5113 | -5640.09 |
假設該筆BBB級貸款價值V服從正態分佈,設貸款價值的均值為\mu,標準差為σ,則:
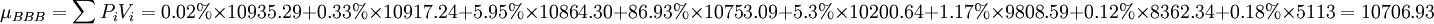 (元)。
(元)。
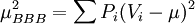
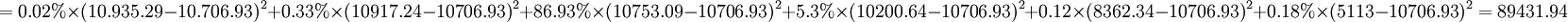
μBBB = 299.05
我們可得出888貸款的價值表,見表6。
表6 該筆貸款的信用風險估值計算表
第一年末信用評級 信用評級概率(%) 貸款價值(元) 概率、加權價值(元) 價值與均值的偏離(元) 概率加權的偏離的平方 AAA 0.02 10935.29 2 228.36 10.43 AA 0.33 10917.24 36 210.31 145.6 A 5.95 10864.3 646 157.37 1473.54 BBB 86.93 10753.09 9348 46.16 1852.26 BB 5.3 10200.64 541 -506.29 13585.47 B 1.17 9808.59 115 -898.34 9442.07 CCC 0.12 8362.34 10 -2344.59 6596.52 違約 0.18 5113 9 -5593.93 56325.7
因此,在正態分佈下,該筆BBB級貸款的信用風險估值如下:
99%置信度的VaR=2.33\times299=697(元)
95%置信度的VaR=1.65\times299=493(元)
計算結果表明,在貸款價值為正態分佈的假設條件下,該筆貸款有1%的可能性在第二年的損失超過697元,有5%的可能性在第二年的損失超過493元。反過來說,該筆貸款在第二年的損失有99%的可能性保證不超過697元,有95%的可能性保證不超過493元。
2.組合貸款或債券情況下的信用風險估值
為簡單起見,假設一個銀行的企業貸款或債券組合只包含兩筆貸款或債券,該組合一筆貸款或債券如上例所示BBB級貸款,第二筆貸款或債券假設為A級的貸款。下麵以上述兩筆貸款來計算組合情況下的信用風險估值問題。
具體步驟為:
(1)推導每一個評級分類的資產收益的閾值
(2)估計每對債務人資產收益之間的相關性
(3)估算組合價值
(4)確定組合未來價值的置信水平分位數
假設第二筆貸款的最初評級為A級,年利率為5%,金額為10000元,期限為5年高級未擔保的不可提前償還貸款,一年後該貸款價格為:。
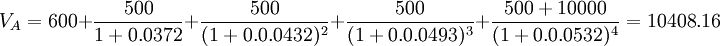 (元)。
(元)。
計算出A級貸款價值分佈,計算結果見表7。
表7 第二筆貸款的價值分佈
| 年末評級 | 貸款價值(元) | 轉移概率 |
| AAA | 10477.66 | 0.09 |
| AA | 10460.02 | 2.27 |
| A | 10408.16 | 91.05 |
| BBB | 10299.66 | 5.52 |
| BB | 9759.27 | 0.74 |
| B | 9375.56 | 0.26 |
| CCC | 7950.18 | 0.01 |
| 違約 | 5113 | 0.06 |
在聯合概率中考慮相關性,利用上面方法計算每個貸款或債券的閥值(見表8),然後根據二元正態分佈計算出聯合概率。同理,假定每個公司的資產價值的正規化對數收益服從正態分佈,對於BBB級和A級這樣兩個債務人來說,假設兩筆貸款回報率的相關性已知,記為ρ,收益率為rBBB和rA,考慮它們的聯合態分佈,其一般密度函數為:
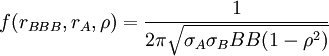
=![exp(-(r^2_A+r^2_{BBB}-2\rho r_A r_{BBB})/[2(1-\rho^2)])](/w/images/math/2/1/c/21caaf95a61c7445c362d51b934c73fe.png)
表8 BBB級和A級兩個債務人的評級轉移概率和信貸質量閥值
| 一年內評級 | BBB級債務人 | A級債務人 | ||
| 概率(%) | 閥值(Z) | 概率(%) | 閥值(Z) | |
| AAA | 0.02 | +∞ | 0.09 | +∞ |
| AA | 0.33 | 3.54 | 2.27 | 3.12 |
| A | 5.95 | 2.7 | 91.05 | 1.98 |
| BBB | 86.93 | 1.53 | 5.52 | -1.51 |
| BB | 5.3 | -1.49 | 0.74 | -2.3 |
| B | 1.17 | -2.18 | 0.26 | -2.72 |
| CCC | 0.12 | -2.75 | 0.01 | 13.19 |
| 違約 | 0.18 | -2.91 | 0.06 | -3.24 |
計算兩筆貸款(BBB級貸款和A級貸款)組合的年末價值見表9。
表9 二筆貸款組合年末價值
| AAA | AA | A | BBB | BB | B | CCC | D | |
| AAA | 21412.95 | 21395.31 | 21343.45 | 21234.95 | 20694.85 | 20310.85 | 18885.47 | 16048.29 |
| AA | 21394.9 | 21377.26 | 21325.4 | 21216.9 | 20676.8 | 20292.8 | 18867.42 | 16030.24 |
| A | 21341.96 | 21324.32 | 21272.46 | 21163.96 | 20623.86 | 20239.86 | 18814.48 | 15977.3 |
| BBB | 21230.75 | 21213.11 | 21161.25 | 21052.75 | 20512.65 | 20128.65 | 18703.27 | 15866.09 |
| BB | 20678.3 | 20660.66 | 20608.8 | 20500.3 | 19960.2 | 19576.2 | 18150.82 | 15313.64 |
| B | 20286.25 | 20268.61 | 20216.75 | 20108.25 | 19568.15 | 19184.15 | 17758.77 | 14921.59 |
| CCC | 18840 | 18822.36 | 18770.5 | 18662 | 19121.9 | 17737.9 | 16312.52 | 13475.34 |
| 違約 | 15590.66 | 15573.02 | 15521.6 | 15415.66 | 14872.56 | 14488.56 | 13063.18 | 10226 |
聯合評級概率的計算。例如,假設資產相關性為20%%,最終評級為BBB_{BBB}和A_A的聯合概率,兩者都維持現有評級不變的概率為:
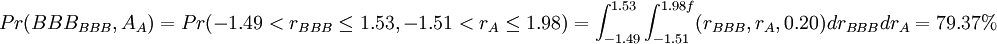
運用聯合違約概率計算聯合違約事件的相關性,我們有:
![\rho(D_{BBB},D_A)=\frac{P(D_{BBB},D_A)-P(D_{BBB})P(D_A)}{\sqrt{P(D_{BBB})[1-P(D_{BBB})]P(D_A)[1-P(D_A)]}}](/w/images/math/4/e/6/4e6ab0e18cf88a2694a0b92cea647caa.png) 。
。
下麵我們假設兩個債券發行公司的資產收益相關性為ρ = 0.40從表7中可知,BBB級和A級的違約概率分別是P(DBBB = 0.18%和P(DA) = 0.06%和,聯合違約概率為:
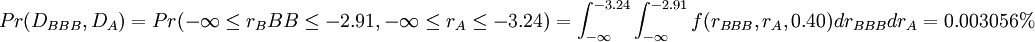
同理,第二筆A級貸款價值的均值為μA標準差σA,則 :
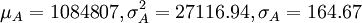
綜上,該兩筆貸款組合的均值為:
μP = μBBB = 10706.93 + 10848.07 = 21555
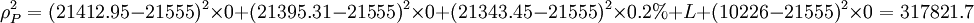
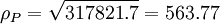
因此,在正態分佈下,該組合貸款的信用風險估值如下:
99%置信度的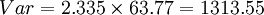 (元)
(元)
95%置信度的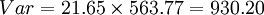 (元)
(元)
CreditMetrics模型的出現標志著風險估值和管理工作在精確性及主動性方面取得了巨大進展,信貸資產或債券的組合風險估值對信用評級更加敏感。該模型主要應用:
一是該模型以分析性框架為基礎,可計算組合價值的波動率和預期損失,也可計算組合內債務人的邊際風險貢獻及組合的多樣化效應。
二是運用蒙特卡羅模擬方法可以進一步估計資產組合的遠期價值分佈,從而確定信貸資產的信用風險值。
三是CreditMetrics的輸出報告在風險管理以及建立對沖策略方面有著非常重要的應用,金融機構能夠評估總體的風險規模,針對可能的不利情況設立相應的資本緩衝,以確保自己能夠在遭受不利的信貸事件時還能繼續生存下去所需的緩衝資本。
- ↑ 李興法,王慶石.基於CreditMetrics模型的商業銀行信用風險應用研究[J].財經問題研究,2006,(12)








本文的definition通俗易懂,感謝各位的編輯。