轉移概率矩陣
出自 MBA智库百科(https://wiki.mbalib.com/)
轉移概率矩陣(Transition Probability Matrix)
目錄 |
轉移概率矩陣:矩陣各元素都是非負的,並且各行元素之和等於1,各元素用概率表示,在一定條件下是互相轉移的,故稱為轉移概率矩陣。如用於市場決策時,矩陣中的元素是市場或顧客的保留、獲得或失去的概率。P(k)表示k步轉移概率矩陣。
轉移概率矩陣有以下特征:
①,0≤Pij≤1
②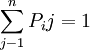 ,即矩陣中每一行轉移概率之和等於1。
,即矩陣中每一行轉移概率之和等於1。
所謂矩陣,是指許多個數組成的一個數表。每個數稱為矩陣的元素。矩陣的表示方法是用括弧將矩陣中的元素括起來,以表示它是一個整體。如A就是一個矩陣。
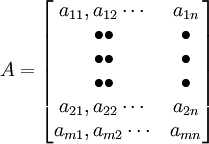
這是一個由m行n列的數構成的矩陣, 表示位於矩陣中第i行與第j列交叉點上的元素, 矩陣中的行數與列數可以相等,也可以不等。當它們相等時,矩陣就是一個方陣。
由轉移概率組成的矩陣就是轉移概率矩陣。也就是說構成轉移概率矩陣的元素是一個個的轉移概率。
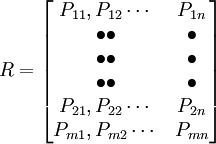
轉移概率與轉移概率矩陣[1]
假定某大學有1萬學生,每人每月用1支牙膏,並且只使用“中華”牙膏與“黑妹”牙膏兩者之一。根據本月(12月)調查,有3000人使用黑妹牙膏,7000人使用中華牙膏。又據調查,使用黑妹牙膏的3000人中,有60%的人下月將繼續使用黑妹牙膏,40%的人將改用中華牙膏; 使用中華牙膏的7000人中, 有70%的人下月將繼續使用中華牙膏,30%的人將改用黑妹牙膏。據此,可以得到如表-1所示的統計表。
表-1 兩種牙膏之間的轉移概率
擬用 黑妹牙膏 中華牙膏 現用 黑妹牙膏 60% 40% 中華牙膏 30% 70%
上表中的4個概率就稱為狀態的轉移概率,而這四個轉移概率組成的矩陣
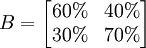
稱為轉移概率矩陣。可以看出, 轉移概率矩陣的一個特點是其各行元素之和為1。 在本例中,其經濟意義是:現在使用某種牙膏的人與將來使用各種品牌牙膏的人數百分比之和為1。
2. 用轉移概率矩陣預測市場占有率的變化
有了轉移概率矩陣,就可以預測,到下個月(1月份)使用黑妹牙膏和中華牙膏的人數,計算過程如下:
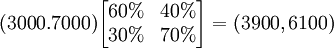
即:1月份使用黑妹牙膏的人數將為3900,而使用中華牙膏的人數將為6100。
假定轉移概率矩陣不變,還可以繼續預測到2月份的情況為:
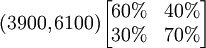
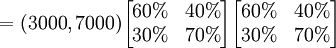
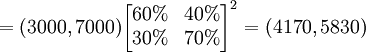
這裡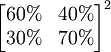 稱為二步轉移矩陣,也即由12月份的情況通過2步轉移到2月份的情況。二步轉移概率矩陣正好是一步轉移概率矩陣的平方。一般地, k步轉移概率矩陣
稱為二步轉移矩陣,也即由12月份的情況通過2步轉移到2月份的情況。二步轉移概率矩陣正好是一步轉移概率矩陣的平方。一般地, k步轉移概率矩陣
正好是一步轉移概率矩陣的k次方。可以證明,k步轉移概率矩陣中,各行元素之和也都為1。
案例一: 用轉移概率矩陣預測市場占有率的變化[1]
有了轉移概率矩陣,就可以預測,到下個月(1月份)使用黑妹牙膏和中華牙膏的人數,計算過程如下:
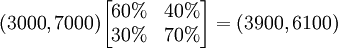
即:1月份使用黑妹牙膏的人數將為3900,而使用中華牙膏的人數將為6100。 假定轉移概率矩陣不變,還可以繼續預測到2月份的情況為:
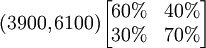
=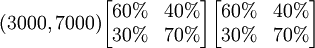
=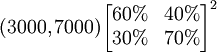
=(4170,5830)
這裡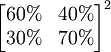
稱為二步轉移矩陣,也即由12月份的情況通過2步轉移到2月份的情況。二步轉移概率矩陣正好是一步轉移概率矩陣的平方。一般地, k步轉移概率矩陣正好是一步轉移概率矩陣的k次方。可以證明,k步轉移概率矩陣中,各行元素之和也都為1。
評論(共16條)
表1中的70%和30%位置反了!
應沒錯,表1左欄的數據表示“現用”,而右欄的數據表“擬用”。
表1中的70%和30%位置反了!
表1中的70%和30%位置反了!
感謝您的指正,經再次驗證,已對數據進行修改。
只有結果啊,算的過程是什麼,就是那個矩陣平方和第一月份結果的運算過程是什麼
3000乘上60%再加上7000乘上30%就等於3900囖
還是有疑問 轉移矩陣的獲得是通過市場調查所得還是也可以由前後相連的兩個時間序列數據所獲得呢?? 還有 不是說馬爾科夫模型一般只適用於短期的趨勢分析與預測嗎??
謝謝,但是想知道矩陣的冪有沒有簡單演算法
用matlab
謝謝,但是想知道矩陣的冪有沒有簡單演算法
用matlab計算








只有結果啊,算的過程是什麼,就是那個矩陣平方和第一月份結果的運算過程是什麼