转移概率矩阵
出自 MBA智库百科(https://wiki.mbalib.com/)
转移概率矩阵(Transition Probability Matrix)
目录 |
转移概率矩阵:矩阵各元素都是非负的,并且各行元素之和等于1,各元素用概率表示,在一定条件下是互相转移的,故称为转移概率矩阵。如用于市场决策时,矩阵中的元素是市场或顾客的保留、获得或失去的概率。P(k)表示k步转移概率矩阵。
转移概率矩阵有以下特征:
①,0≤Pij≤1
②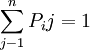 ,即矩阵中每一行转移概率之和等于1。
,即矩阵中每一行转移概率之和等于1。
所谓矩阵,是指许多个数组成的一个数表。每个数称为矩阵的元素。矩阵的表示方法是用括号将矩阵中的元素括起来,以表示它是一个整体。如A就是一个矩阵。
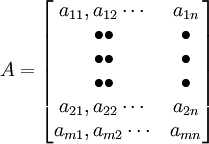
这是一个由m行n列的数构成的矩阵, 表示位于矩阵中第i行与第j列交叉点上的元素, 矩阵中的行数与列数可以相等,也可以不等。当它们相等时,矩阵就是一个方阵。
由转移概率组成的矩阵就是转移概率矩阵。也就是说构成转移概率矩阵的元素是一个个的转移概率。
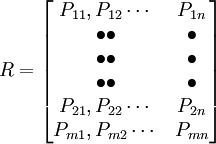
转移概率与转移概率矩阵[1]
假定某大学有1万学生,每人每月用1支牙膏,并且只使用“中华”牙膏与“黑妹”牙膏两者之一。根据本月(12月)调查,有3000人使用黑妹牙膏,7000人使用中华牙膏。又据调查,使用黑妹牙膏的3000人中,有60%的人下月将继续使用黑妹牙膏,40%的人将改用中华牙膏; 使用中华牙膏的7000人中, 有70%的人下月将继续使用中华牙膏,30%的人将改用黑妹牙膏。据此,可以得到如表-1所示的统计表。
表-1 两种牙膏之间的转移概率
拟用 黑妹牙膏 中华牙膏 现用 黑妹牙膏 60% 40% 中华牙膏 30% 70%
上表中的4个概率就称为状态的转移概率,而这四个转移概率组成的矩阵
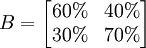
称为转移概率矩阵。可以看出, 转移概率矩阵的一个特点是其各行元素之和为1。 在本例中,其经济意义是:现在使用某种牙膏的人与将来使用各种品牌牙膏的人数百分比之和为1。
2. 用转移概率矩阵预测市场占有率的变化
有了转移概率矩阵,就可以预测,到下个月(1月份)使用黑妹牙膏和中华牙膏的人数,计算过程如下:
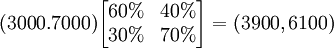
即:1月份使用黑妹牙膏的人数将为3900,而使用中华牙膏的人数将为6100。
假定转移概率矩阵不变,还可以继续预测到2月份的情况为:
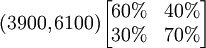
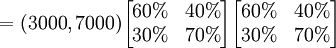
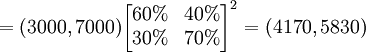
这里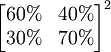 称为二步转移矩阵,也即由12月份的情况通过2步转移到2月份的情况。二步转移概率矩阵正好是一步转移概率矩阵的平方。一般地, k步转移概率矩阵
称为二步转移矩阵,也即由12月份的情况通过2步转移到2月份的情况。二步转移概率矩阵正好是一步转移概率矩阵的平方。一般地, k步转移概率矩阵
正好是一步转移概率矩阵的k次方。可以证明,k步转移概率矩阵中,各行元素之和也都为1。
案例一: 用转移概率矩阵预测市场占有率的变化[1]
有了转移概率矩阵,就可以预测,到下个月(1月份)使用黑妹牙膏和中华牙膏的人数,计算过程如下:
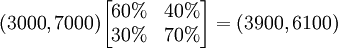
即:1月份使用黑妹牙膏的人数将为3900,而使用中华牙膏的人数将为6100。 假定转移概率矩阵不变,还可以继续预测到2月份的情况为:
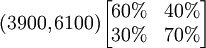
=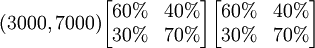
=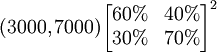
=(4170,5830)
这里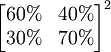
称为二步转移矩阵,也即由12月份的情况通过2步转移到2月份的情况。二步转移概率矩阵正好是一步转移概率矩阵的平方。一般地, k步转移概率矩阵正好是一步转移概率矩阵的k次方。可以证明,k步转移概率矩阵中,各行元素之和也都为1。
评论(共16条)
表1中的70%和30%位置反了!
应没错,表1左栏的数据表示“现用”,而右栏的数据表“拟用”。
表1中的70%和30%位置反了!
表1中的70%和30%位置反了!
感谢您的指正,经再次验证,已对数据进行修改。
只有结果啊,算的过程是什么,就是那个矩阵平方和第一月份结果的运算过程是什么
3000乘上60%再加上7000乘上30%就等于3900囖
还是有疑问 转移矩阵的获得是通过市场调查所得还是也可以由前后相连的两个时间序列数据所获得呢?? 还有 不是说马尔科夫模型一般只适用于短期的趋势分析与预测吗??
谢谢,但是想知道矩阵的幂有没有简单算法
用matlab
谢谢,但是想知道矩阵的幂有没有简单算法
用matlab计算








只有结果啊,算的过程是什么,就是那个矩阵平方和第一月份结果的运算过程是什么