損失函數
出自 MBA智库百科(https://wiki.mbalib.com/)
損失函數(Loss Function)
目錄 |
損失函數(loss function)或代價函數(cost function)是將隨機事件或其有關隨機變數的取值映射為非負實數以表示該隨機事件的“風險”或“損失”的函數。在應用中,損失函數通常作為學習準則與優化問題相聯繫,即通過最小化損失函數求解和評估模型。例如在統計學和機器學習中被用於模型的參數估計(parametric estimation) ,在巨集觀經濟學中被用於風險管理(risk management)和決策 ,在控制理論中被應用於最優控制理論(optimal control theory)。
損失函數是指一種將一個事件(在一個樣本空間中的一個元素)映射到一個表達與其事件相關的經濟成本或機會成本的實數上的一種函數,較常運用在統計學,統計決策理論和經濟學中。損失函數參數的真值為(θ),決策的結果為d ,兩者的不一致會帶來一定的損失,這種損失是一個隨機變數,用L(θ,d)表示。
常見的損失函數有L(θ,d) = c(θ − d)2(稱為二次損失函數)和L(θ,d) = c | θ − d | (稱為絕對損失函數)。
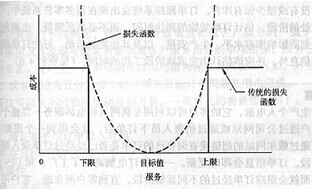
損失函數是描述系統在不同參數(parameter)值之下的損失。要應用損失的函數,其損失必須是通過某種媒介可以衡量的。
損失函數在實踐中最重要的運用,在於協助我們通過過程的改善而持續減少目標值的變異,並非僅僅追求符合邏輯。
現在舉個例子:某個工廠人員的產出,以每小時多少元來計算,而損失函數所顯示的,是產出以室內通風條件而改變的情形。廠內工作的每個人,都有自己的損失函數。為了簡化說明,假設每個人的損失函數均為一條拋物線,其底部一點代表產出值最大時的通風條件,把所有人員的損失函數進行疊加,公司整體的損失函數也必然是一條拋物線。如果通風條件偏離這個最佳水準,就會有額外損失發生。當該拋物線與橫軸相切時,切點的左右各有一小段與橫軸幾近重合。也就是說,由最適點偏離一小短距離,損失小到可以忽略不計。因此,當室內通風條件稍稍偏離均衡點,發生的損失可以忽略不計。但是遠離均衡點時,總是有人必須支付這損失。如果我們能夠導出有具體數字的損失函數,我們就可以計算出最優均衡點,在均衡點中最適合的通風條件如何,以及達到要求的費用支出是多少。
隨著服務偏離目標值,損失會遞增。遞增速度如下:
L=k(y-m)2
L——以美元表示的單位損失(懲罰成本)
y——質量變數的值
m——質量變數y的目標值
k——常數,取決於質量變數在財務上的重要性。
某匹薩外賣店承諾在接到訂單30分鐘內送貨。如果超過承諾時間10分鐘,那麼將賠償金額3美元。送貨成本大概是2美元,但是,隨著送貨時間的推遲,送貨成本將以0.15美元/分鐘的速度下降。實際送貨時間應偏離目標送貨時間多長,能使成本最低?
總成本(N)=送貨成本(J)+賠償成本(L)
設實際送貨時間為y
送貨成本J=2-0.15(y-30)
賠償成本L=k(y-30)2
N=L+J=k(y-30)2+[2-0.15(y-30)]
首先求出k,再求出Min(N)。如何求k?
L=k(y-30)2
3=k(10-0)2

Min(N)=Min{0.03(y-30)2+[2-0.15(y-30)]}
求導,得出y-30=2.5,即實際送貨時間不偏離目標時間2.5分鐘以上。