ARIMA模型
出自 MBA智库百科(https://wiki.mbalib.com/)
自回歸移動平均模型(Autoregressive Integrated Moving Average Model,簡記ARIMA)
目錄 |
ARIMA模型全稱為自回歸移動平均模型(Autoregressive Integrated Moving Average Model,簡記ARIMA),是由博克思(Box)和詹金斯(Jenkins)於70年代初提出的一著名時間序列預測方法,所以又稱為box-jenkins模型、博克思-詹金斯法。其中ARIMA(p,d,q)稱為差分自回歸移動平均模型,AR是自回歸, p為自回歸項; MA為移動平均,q為移動平均項數,d為時間序列成為平穩時所做的差分次數。
ARIMA模型的基本思想是:將預測對象隨時間推移而形成的數據序列視為一個隨機序列,用一定的數學模型來近似描述這個序列。這個模型一旦被識別後就可以從時間序列的過去值及現在值來預測未來值。現代統計方法、計量經濟模型在某種程度上已經能夠幫助企業對未來進行預測。
(一)根據時間序列的散點圖、自相關函數和偏自相關函數圖以ADF單位根檢驗其方差、趨勢及其季節性變化規律,對序列的平穩性進行識別。一般來講,經濟運行的時間序列都不是平穩序列。
(二)對非平穩序列進行平穩化處理。如果數據序列是非平穩的,並存在一定的增長或下降趨勢,則需要對數據進行差分處理,如果數據存在異方差,則需對數據進行技術處理,直到處理後的數據的自相關函數值和偏相關函數值無顯著地異於零。
(三)根據時間序列模型的識別規則,建立相應的模型。若平穩序列的偏相關函數是截尾的,而自相關函數是拖尾的,可斷定序列適合AR模型;若平穩序列的偏相關函數是拖尾的,而自相關函數是截尾的,則可斷定序列適合MA模型;若平穩序列的偏相關函數和自相關函數均是拖尾的,則序列適合ARMA模型。
(四)進行參數估計,檢驗是否具有統計意義。
(五)進行假設檢驗,診斷殘差序列是否為白雜訊。
(六)利用已通過檢驗的模型進行預測分析。
| Glossary of statistical terms | |
|---|---|
| Language | Description |
| English | Box-Jenkins model |
| French | modèle de Box-Jenkins |
| German | Box-Jenkins-Modell |
| Dutch | Box-Jenkins-model |
| Italian | modello Box-Jenkins |
| Spanish | modelo de Box-Jenkins |
| Catalan | model de Box-Jenkins |
| Romanian | modelul Box-Jenkins |
| Finnish | Boxin-Jenkinsin mallit |
| Hungarian | Box-Jenkins-modell |
| Turkish | Box-Jenkins modeli |
| Estonian | Box-Jenkinsi mudel |
| Lithuanian | Box ir Jenkins modelis ; Bokso ir Dženkinso modelis |
| Slovenian | Box-Jenkinsova model |
| Polish | model Boxa-Jenkinsa |
| Russian | Модель Бокса-Дженкинса |
| Ukrainian | модель Бокса - Дженкінса |
| Farsi | modele Box-Jenkins |
| Persian-Farsi | مدل باکس-جنکينز |
| Arabic | نموذج بوكس - جنكز |
| Afrikaans | Box-Jenkins-model |
| Chinese | 博克斯―詹金斯模型 |
2008年。海關稅收預算計劃8400億元.比2007年實際完成數增加10.8%,比2007年預算數增加22.1%。為了對2008年江門海關稅收總體形勢進行把握,筆者嘗試利用SAS統計分析軟體的時間序列預測模塊建立ARIMA模型,對2008年江門海關稅收總值進行預測。從預測結果來看,預測模型擬合度較高,預測值也切合實際情況,預測模型具有一定的應用價值。現將預測的方法、原理以及影響稅收工作的相關因素分析。
一、ARlMA模型原理
ARIMA模型全稱為自回歸移動平均模型(Autoregressive Integrated Moving Average Model,簡記ARIMA)。是由博克思(Box)fFfl詹金斯(Jenkins)於70年代初提出的一著名時問序列預測方法,所以又稱為box--jenkins模型、博克思一詹金斯法。其中ARIMA(p,d.q)稱為差分自回歸移動平均模型,AR是自回歸,P為自回歸項;MA為移動平均,q為移動平均項數,d為時間序列成為平穩時所做的差分次數。ARIMA模型可分為3種:(1)自回歸模型(簡稱AR模型);(2)滑動平均模型(簡稱MA模型);(3)自回歸滑動平均混合模型(簡稱ARIMA模型)。
ARIMA模型的基本思想是:將預測對象隨時問推移而形成的數據序列視為—個隨機序列.以時間序列的自相關分析為基礎.用一定的數學模型來近似描述這個序列。這個模型一旦被識別後就可以從時間序列的過去值及現在值來預測未來值。ARlMA模型在經濟預測過程中既考慮了經濟現象在時間序列上的依存性,又考慮了隨機波動的干擾性,對於經濟運行短期趨勢的預測準確率較高,是近年應用比較廣泛的方法之一。
二、應用ARIMA模型進行預測
每月稅收數據.可以看作是隨著時間的推移而形成的一個隨機時間序列,通過對該時間序列上稅款值的隨機性、平穩性以及季節性等因素的分析,將這些單月稅收值之間所具有的相關性或依存關係用數學模型描述出來,從而達到利用過去及現在的稅收值信息來預測未來稅收情況的目的。
(一)對序列取對數和作差分處理,形成穩定隨機序列
ARIMA模型建模的基本條件是要求待預測的數列滿足平穩的條件,即個體值要圍繞序列均值上下波動,不能有明顯的上升或下降趨勢,如果出現上升或下降趨勢,需要對原始序列進行差分平穩化處理。
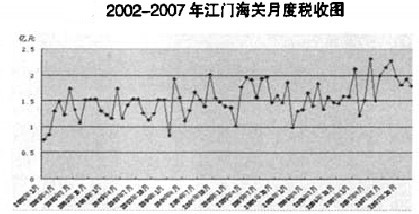
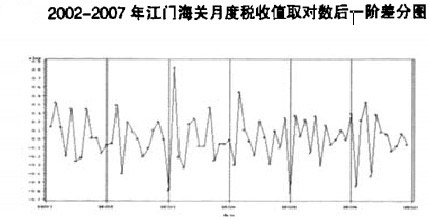
從上圖可看出,江門海關自2002年以來的實際入庫稅收值數列波動性較明顯,且呈現出一定的上升趨勢,不能直接用ARIMA模型進行建模。取對數可以消除數據波動變大趨勢,對數列進行一階差分,可以消除數據增長趨勢性和季節性。從下圖可以看出,預測數列取對數並作一階差分後的圖形顯示基本消除了長期趨勢性的影響,趨於平穩化,滿足ARIMA模型建模的基本要求。
(二)模型參數的估計
時間序列預測模塊的自相關分析包括對自相關係數和偏相關係數的分析,通過對比分析從而實現對時間序列特性的識別。從計算結果可知,自相關函數1步截尾,偏自相關函數2步截尾,白相關函數通過白雜訊檢驗。根據變換數列的自相關函數和偏自相關函數的特點,並經過反覆測試,對ARIMA模型的參數進行估計.三個參數定為d=l,p=2和q=l。
對參數進行檢驗。從檢驗結果可知,參數估計全部通過顯著性檢驗.擬合優度統計量表中給出了殘差序列的方差(0.063367)和標準誤差(0.251729),以及按AIC和SBC標準計算的統計量(9.496798)和(18.54752),這兩個值都較小,表明對預測模型擬合得較好。從殘差的自相關檢驗結果數據中.可以得知殘差通過白雜訊顯著性檢驗。預測模型最終形式為:(14-0.98284B)(1+0.56103B-2)Z=(1-0.34111B)(1+B)u其中,Z=logX。B為後移運算元,u為隨機干擾項(三)應用模型預測。
利用上面確定的模型進行預測。預測模型x.-J 2007年稅收的擬合值是21.75億元,跟實際稅收值22.58億元比較,誤差為3.7%,表明預測模型擬合度較高,預測模型具有一定的應用fir值。把預測模型向前推12個月進行預測,得到2008年各月稅收數據,全年累計稅收預計均值為23.5億元,實際稅收值會圍繞此值上下波動。需要說明的是,由於利用模型向前預測1一12月的數據,預測時間越長,難度越大,預測精度也下降,若到年中再次預測時,預測精度將會進一步提高。
這個稅收預測值是基於當前海關監管水平、稅收徵管水平不變或提高的基礎上,挖掘稅收樣本數據自身涵蓋的信息.利用數理統計分析方法,建立預測模型得出的理論預測值,一旦實際外部環境和條件發生變化,例如國家實施巨集觀調控、人民幣升值過快、匯率大幅變動、對外經濟政策的變化等,將對稅收預測結果生一定的影響。
三、其他可能對2008年稅收工作產生影響的主要因素
(一)個別商品稅收變化影響巨大
2007年占關區稅收總值80%前20位大類稅源商品,與2006年占關區稅收總值80%前20位大類稅源商品相比,新增了大豆、印刷和裝訂機械及零件、棉紗線,少了空氣調節器、初級形狀的聚丙烯和初級形狀的聚乙烯.新增的三項商品稅收總值為3.1億元。占關區稅收總值13.8%,其中,大豆2007年稅款高達2.6億元,2006年僅為15萬元,影響巨大。另外,煤和鋼材的稅收值大幅增長。液化石油氣、紡織品(包括服裝和紡織紗線)、紙及紙板(未切成形的)稅收下降幅度較大。
主要稅源商品的不穩定,為關區稅收工作增加了難度。
(二)本地企業異地納稅仍保持較大規模
據統計,2007年江門關區企業在異地進口異地報關應稅貨值85.2億元人民幣,比2006年增長13.6%,應徵稅收為9.2億元,較2006年增長7.4%.占江門區同期應徵稅收總額的四成多。
從口岸分佈來看,大部分本地企業異地納稅進口行為分佈在廣州口岸。在廣州口岸納稅4.7億元,下降占異地納稅總值的51.1%。另外。在黃埔口岸納稅1.7億元,下降4.8%;在拱北口岸納稅1.3億元,增加3倍從商品來看,異地納稅進口的商品主要是廢塑料、廢五金、木漿、冰乙酸、正丁醇、脂肪醇、凍豬雜碎、IEl挖掘機、初級形狀聚乙烯等商品,稅款均超過千萬元,部分商品曾經在本關區口岸大量進口。廢塑料進口3億元,下降10.9%;廢五金進口1.2億元,增長87.6%;木漿進口7783萬元,增長17.2%;冰乙酸進口6593萬元,下降19.4%;正丁醇進口3498萬元,增長3.5倍;脂肪醇進口3366萬元。32.3%;凍豬雜碎進口3313萬元,增長2.3倍;舊挖掘機進口3101萬元,下降1.7%;初級形狀聚乙烯進口2539萬元,下降54%。其中正丁醇、凍豬雜碎和廢五金進口增長迅猛。
(三)主要納稅大戶變化較大
2007年占關區稅收總值60%前20位納稅企業,與2006年占關區稅收總值60%前20位納稅企業相比,有12家企業新上榜,更新率為60%。新增的2家納稅企業嘉吉投資(中國)有限公司和北京華特安科經貿有限公司共納稅3.4億元,占關區稅收總值的15%。影響巨大。而海洋石油陽江實業有限公司的納稅額從2006年的1.4億元下降到2783萬元,該企業的稅款下fl手x,l 2007年關區稅收工作帶來了較大的影響。主要納稅大戶的不穩定,加大了2008年關區稅收工作的不確定性。
(四)加工貿易內銷補稅和出口徵稅的影響
2007年,江門關區一般貿易應徵稅收為21.5億元,增長26.5%;加工貿易內銷補稅(不含後續補稅)為7909萬元,增長11.3%;後續補稅為594萬元,增長49.3%。2007年江門關區出口商品徵稅160萬元,增長1.8倍。江門關區的稅收以一般貿易進口徵稅為主,但由於加工貿易進出口值占關區進出口總值的比重超過一半.因而加強加工貿易內銷徵稅工作,充分挖掘加貿內銷補稅潛力,可以為關區稅收總量增長提供支持。雖然當前出口徵稅占關區稅收總值的比重非常少,但由於國家不斷調整外貿政策,2008年出口需要征收關稅商品涉及300多個稅號,而且相當多的商品出口關稅率高達15—20%,預計江門關區出口關稅將會保持大幅增長態勢,為關區稅收總量增長提供補充。
綜合來看,只要大類稅源商品如己內酰胺、大豆、煤、鋼材和廢紙等保持2007年的進口規模,其他稅源商品進口沒有大幅下降,2008年的稅收總額就能夠保持甚至超過2007年的稅收水平,如果液化石油氣、紡織品和紙及紙板恢復2006年的進口水平,同時將本關區企業從異地報關引導回本關區報關,今年稅收總額將比2007年小幅增長。結合應用前面的時間序列模型的預測結果,綜合多方面因素,預計全年累計稅收均值為23.5億元。
案例二:基於ARIMA模型的備件消耗預測方法[1]
一、引言
隨著技術的進步和軍事的變革,快速響應戰場需求是裝備戰鬥力的重要指標之一。要快速響應戰場需求就要有強有力的後勤保障和支持,部隊需要保證有一定數量備件。而實際中卻常常由於沒有足夠的備件導致裝備不能快速形成戰鬥力。由於造成備件短缺的重要原因是使用的備件需求預測方法和模型不夠精確[2],故嘗試用差分自回歸滑動平均模型,即ARIMA(p,d,q)模型,對備件消耗進行預測。
1備件消耗預測的ARIMA(p,d,q)模型求和自回歸滑動平均模型(AutoregressiveIntegrated Moving Average Model,簡稱ARIMA),由Box和Jenkins於70年代初提出的時間序列預測方法,又稱為B-J模型、博克思-詹金斯法[3]。其中ARIMA(p,d,q)稱為差分自回歸滑動平均模型,AR是自回歸,MA為滑動平均,p、q分別為對應的階數,d為時間序列成為平穩時所做的差分次數。
1.基本思路
首先需要明確建立模型的前提是在預測的這段時間內,影響該類備件消耗量的主要因素不發生大變故。在此前提下,將備件消耗的歷史統計數據視為一個時間序列,即為一組依賴於時間t的隨機變數序列。這些變數間有依存性和相關性,並表現出一定的規律性,如能根據這些消耗數據建立儘可能合理的統計模型,就能用這些模型來解釋數據的規律性,就可利用已得到的備件消耗數據來預測未來消耗數據,也就能得出備件需求做好的備件供應。
2.模型描述
備件消耗預測ARIMA(p,d,q)模型實質是先對非平穩的備件消耗歷史數據Yt進行d(d=0,1,dots,n)次差分處理得到新的平穩的數據序列Xt,將Xt擬合ARMA(p,q)模型,然後再將原d次差分還原,便可以得到Y_t的預測數據。其中,ARMA(p,q)的一般表達式為:
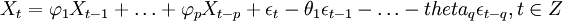 (1)
(1)
式中,前半部分為自回歸部分,非負整數p為自回歸階數,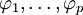 為自回歸繫數,後半部分為滑動平均部分,非負整數q為滑動平均階數,
為自回歸繫數,後半部分為滑動平均部分,非負整數q為滑動平均階數,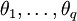 為滑動平均繫數;Xt為備件消耗數據相關序列,εt為WN(0,σ2)。
為滑動平均繫數;Xt為備件消耗數據相關序列,εt為WN(0,σ2)。
當q=0時,該模型成為AR(p)模型: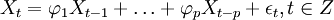 (2)
(2)
當p=0時,該模型成為MA(q)模型: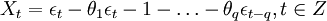 (3)
(3)
3.備件消耗預測建模流程
通過建立ARIMA(p,d,q)模型進行備件消耗預測的基本流程,如下圖。
(1)獲取數據併進行預處理.收集裝備使用階段某備件消耗的數據序列,記為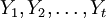 。利用游程檢驗法[4]來判斷該序列是否為平穩序列,如為非平穩序列,用差分的方法,即:
。利用游程檢驗法[4]來判斷該序列是否為平穩序列,如為非平穩序列,用差分的方法,即: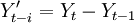 ,對序列進行平穩化預處理,每次差分後數據進行游程檢驗,直到差分所得數據可以通過平穩性檢驗,記為d次差分,得到新的平穩序列
,對序列進行平穩化預處理,每次差分後數據進行游程檢驗,直到差分所得數據可以通過平穩性檢驗,記為d次差分,得到新的平穩序列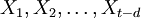 。
。
取前N組(或全部)數據作為觀測數據,進行零均值化處理,即: ,得到一組預處理後的新序列
,得到一組預處理後的新序列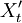 。
。
(2)ARMA模型的識別
通過計算預處理後的序列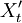 的自相關函數(ACF)
的自相關函數(ACF)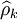 和偏自相關函數(PACF)
和偏自相關函數(PACF)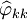 來進行模型識別。具體的計算公式為:
來進行模型識別。具體的計算公式為:
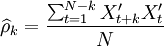 (4)
(4)
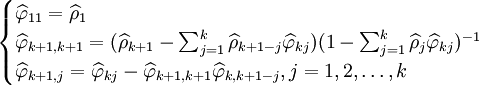 。
。
根據上述計算結果,並依據表1的模型識別原則,可以確定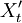 符合的模型。
符合的模型。
ARMA(p,q)模型識別原則
| 模型 | AR(p) | MA(q) | ARMA(p.q) |
| 自相關函數 | 拖尾,指數衰減或振蕩 | 有限長度,截尾(q步) | 拖尾,指數衰減或振蕩 |
| 偏自相關函數 | 有限長度,截尾(p步) | 拖尾,指數衰減或振蕩 | 拖尾,指數衰減或振蕩 |
(3)參數估計和模型定階
參數估計和模型定階是建立備件消耗預測模型的重要內容,二者相互影響。
在上述模型識別的基礎上,利用樣本矩估計法、最小二乘估計法或極大似然估計法等對ARMA(p,q)的未知參數,即自回歸繫數、滑動平均繫數以及白雜訊方差進行估計,得出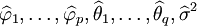 。
。
利用AIC、BIC準則進行模型定階。具體步驟[5]。
(4)模型檢驗
首先要檢驗所建立模型是否能滿足平穩性和可逆性,既要求下式(6)、式(7)根在單位圓外,具體公式如下:
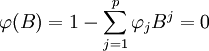 (6)
(6)
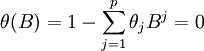 (7)
(7)
再進一步判斷上述模型的殘差序列是否為白雜訊,如果不是,則需要重新進行模型識別,如果是,則通過檢驗,得出軟體可靠性預測模型:
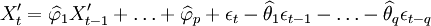 (8)
(8)
(5)備件消耗量預測
根據上述預測模型,依據一步預測的方法對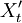 進行預測,並考慮前面所進行的d次差分,還原為備件消耗數據Yt的預測結果,根據該預測結果來進行備件的配置。
進行預測,並考慮前面所進行的d次差分,還原為備件消耗數據Yt的預測結果,根據該預測結果來進行備件的配置。
二、案例應用
1.原始數據及預處理
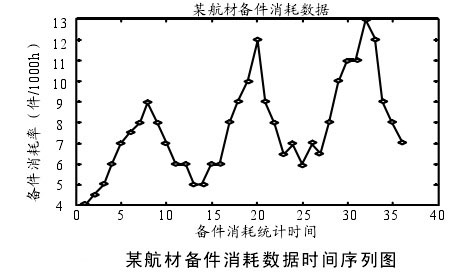
以航空兵場站某種航材備件3年的消耗率(件/1000h)[6]來進行分析和預測。取前30組數據建立模型,並用後面的幾組數據對模型進行預測驗證。
3年的原始數據的時間序列如下圖,是有關備件消耗統計時間(2001年1月到2003年12月)-備件消耗率(件/1000h)的某航材備件消耗數據。
從上圖中可以看出,數據有明顯遞增的趨勢,為非平穩序列。嘗試進行一次差分對數據進行平穩化處理,結果表明仍未平穩,然後再做一次差分,再對進行2次差分後的數據進行游程檢驗[4],可以通過檢驗,故接受數據具有平穩性的原假設。可得出d等於2,並將數據進行零均值化,下麵進一步確定ARMA(p,q)模型。
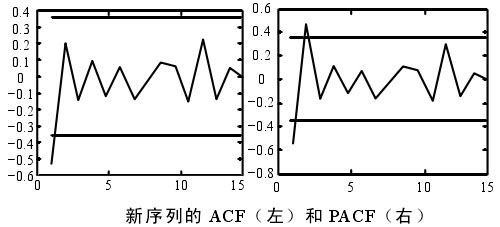
2.建立模型併進行參數估計
計算零均值化後序列的自相關函數(ACF)和偏自相關函數(PACF),結果如下圖。其中,上下兩條線為置信區間(±1.96/ )。由圖可以看出0≤p≤3,0≤q≤2。嘗試建立ARMA(p,q)模型。
)。由圖可以看出0≤p≤3,0≤q≤2。嘗試建立ARMA(p,q)模型。
對p、q可能的組合進行參數估計,並利用AIC準則進行定階,並對估計出的參數進行平穩性和可逆性檢驗,結果表明都在單位圓外,可以初步確定滿足要求的最佳模型為ARMA(3,1)模型,即:
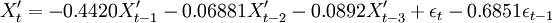 (9)
(9)
式(9)中{εt}為WN(0,1.0943)。
3.白雜訊檢驗
對已經通過平穩性和可逆性檢驗的模型(9)進行白雜訊檢驗(4≤m≤6),檢驗結果如圖4。
由上圖中檢驗結果可看出,對應於上面m的值,都有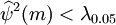 (m),可通過白雜訊檢驗,模型合理。
(m),可通過白雜訊檢驗,模型合理。
4.預測及結果分析
根據模型(9),用一步預測的方法對後4組數據進行預測,並與移動平均法進行對比,如表2。對預測結果進行多角度評價,具體選用的指標包括:平均絕對誤差:
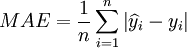 (10)
(10)
平均相對誤差:
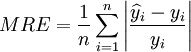 (11)
(11)
預測均方差:
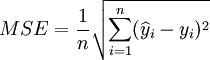 (12)
(12)
其中,y_i為備件消耗序列的實際數據,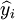 為模型預測數據。
為模型預測數據。
預測結果對比
| 時間 | 真實值 | 移動平均法[5] | ARIMA模型 | ||||||
| 預測值 | MAE | MRE | MSE | 預測值 | MAE | MRE | MSE | ||
| 2003.09 | 12 | 7.2447 | 2.0621 | 21.83% | 1.3524 | 13.4777 | 0.6922 | 6.93% | 0.4298 |
| 2003.10 | 9 | 8.7642 | 9.8088 | ||||||
| 2003.11 | 8 | 8.8250 | 7.7322 | ||||||
| 2003.12 | 7 | 9.4324 | 6.7857 | ||||||
註釋:[5]是[7]
由上表預測結果及各項評價指標的對比可知,ARIMA模型預測結果明顯優於移動平均法,從平均相對誤差上來看,ARIMA模型為6.93%,比移動平均法提高了將近15%,且預測的均方差也較小,僅0.4298。由此可見:該模型能較準確地預測出備件消耗的變化趨勢,可為備件消耗量的預測提供依據。
另由於ARIMA模型建立在歷史數據的基礎上,故搜集的歷史數據越多,模型越準確。
該建模方法能綜合反映裝備使用的實際情況,具有很好的模型適應性。模型具有較高的預測準確度,且有較成熟的軟體支持(SPSS、Matlab等),易於推廣,可進行備件消耗預測,確定備件需求。
- ↑ 賈治宇,康銳.基於ARIMA模型的備件消耗預測方法[J].兵工自動化,2009,28(6)
- ↑ Hua-kai Chiou,Gwo-Hshiung.Grey Prediction Model Forthe Planning Material of Equipment Spare parts in Navy ofTaiwan[C].Proceedings of World Automation Congress,2004(17):315-320
- ↑ George E.P.Box,Gwilym M.Jenkins.時間序列分析-預測與控制[M].北京:中國統計出版社,1997:101-149
- ↑ 4.0 4.1 張樹京,齊立心.時間序列分析簡明教程[M].北京:北方交通大學出版社,2003:24-59
- ↑ 王煒炘,杜金觀,伍尤桂,等.應用時間序列分析[M].桂林:廣西師範大學出版社,1999:102-183
- ↑ 左召軍,鐘新輝.航材消耗的時間序列分析[J].長沙:航空職業技術學院學報,2004,4(3):29-32
- ↑ Craig C,Sherbrooke.Optimal Inventory Modeling of Systems:Multi-Echelon Techniques[M].Boston:Kluwer Academic Pub,2004
本条目由以下用户参与贡献
蔓草寒烟,苦行者,Vulture,Angle Roh,funwmy,Zfj3000,Cabbage,Dan,Guaigui,Fghghg,Yixi,咪小鸭,Breakinen,连晓雾,y桑,nonameh.評論(共16條)
案例預測精度不高 另外對於季節性arima模型也無介紹,acf、pacf也無圖可參考,可以改進 當然,有個參考已經是很好的了,謝謝編輯人員!
博主,你d=2,二階差分,應該是二階導,你怎麼模型公式寫的是一階導’
沒有錯啊,它先做一次差分,再進行2次差分後,對數據進行游程檢驗檢驗得出,d=2,然後才用數據進行零均值化的求導。










太不專業了,怎麼連個數學公式都沒有明確寫出來。文字表述再多也不行啊。