最小二乘估計
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
(重定向自最小二乘估计法)
最小二乘估計 (least-squares estimation)是一個經濟術語。
目錄 |
[編輯]
最小二乘估計是高斯,C.F.(Gauss,Carl Friedrich) 在1974年提出的參數估計法，其特點是演算法簡單，不必知道被估計量及量測量有關的統計信息。
設第i次量測Zi為
Zi = HiX + Vi
式中：Zi為mi維向量；Hi、Vi為第i次量測的量測矩陣和隨機量測雜訊。
描述r次量測的量測方程為
Z = HX + V
式中：Z、V為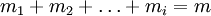
維向量，H為m×n矩陣。
[編輯]
最小二乘估計指標是，使各次量測Zi與由估計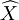
確定的量測的估計
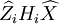均方和最小，即
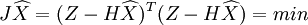
X的最小二乘估計為
[編輯]
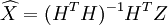
最小二乘估計的性質是，若量測雜訊V是均值為零，方差為R的隨機向量，則
（1）最小二乘估計是無偏估計，即
![E[\widehat{X}]=X](/w/images/math/a/7/a/a7a62fa4f3edfa81fdef7db236525b5e.png)
或
![E[\widehat{X}]=0](/w/images/math/0/4/2/0425de94e0a12f98f65e0e3ed447f2ca.png)
式中：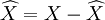
為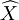的估計誤差。
（2）最小二乘估計的均方誤差陣為
![E[\widehat{X}\widehat{X}^T]=(H^TH)^{-1}H^TRH(H^TH)^{-1}](/w/images/math/4/f/7/4f707c1a960e53daaa5af6268d0ca51a.png)
評論(共4條)
121.34.145.* 在 2017年6月5日 11:16 發表
最小二乘估計是高斯在1975年提出的參數估計法--->不要誤導好吧，此高斯非彼高斯呀！1794年德國數學家C.F.高斯在解決行星軌道猜測問題時首先提出最小二乘法。
120.42.91.* 在 2017年6月6日 09:28 發表
121.34.145.* 在 2017年6月5日 11:16 發表
最小二乘估計是高斯在1975年提出的參數估計法--->不要誤導好吧，此高斯非彼高斯呀！1794年德國數學家C.F.高斯在解決行星軌道猜測問題時首先提出最小二乘法。
應該是重定向錯誤了，確實不是同一個，俺順手改了
講的不是很通俗易懂 可以結合圖來說明最小二乘法的用法呵