最小二乘估计
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
最小二乘估计 (least-squares estimation)是一个经济术语。
目录 |
[编辑]
最小二乘估计是高斯,C.F.(Gauss,Carl Friedrich) 在1974年提出的参数估计法，其特点是算法简单，不必知道被估计量及量测量有关的统计信息。
设第i次量测Zi为
Zi = HiX + Vi
式中：Zi为mi维向量；Hi、Vi为第i次量测的量测矩阵和随机量测噪声。
描述r次量测的量测方程为
Z = HX + V
式中：Z、V为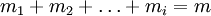
维向量，H为m×n矩阵。
[编辑]
最小二乘估计指标是，使各次量测Zi与由估计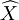
确定的量测的估计
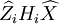均方和最小，即
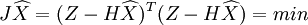
X的最小二乘估计为
[编辑]
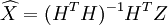
最小二乘估计的性质是，若量测噪声V是均值为零，方差为R的随机向量，则
（1）最小二乘估计是无偏估计，即
![E[\widehat{X}]=X](/w/images/math/a/7/a/a7a62fa4f3edfa81fdef7db236525b5e.png)
或
![E[\widehat{X}]=0](/w/images/math/0/4/2/0425de94e0a12f98f65e0e3ed447f2ca.png)
式中：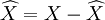
为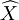的估计误差。
（2）最小二乘估计的均方误差阵为
![E[\widehat{X}\widehat{X}^T]=(H^TH)^{-1}H^TRH(H^TH)^{-1}](/w/images/math/4/f/7/4f707c1a960e53daaa5af6268d0ca51a.png)
评论(共4条)
121.34.145.* 在 2017年6月5日 11:16 发表
最小二乘估计是高斯在1975年提出的参数估计法--->不要误导好吧，此高斯非彼高斯呀！1794年德国数学家C.F.高斯在解决行星轨道猜测问题时首先提出最小二乘法。
120.42.91.* 在 2017年6月6日 09:28 发表
121.34.145.* 在 2017年6月5日 11:16 发表
最小二乘估计是高斯在1975年提出的参数估计法--->不要误导好吧，此高斯非彼高斯呀！1794年德国数学家C.F.高斯在解决行星轨道猜测问题时首先提出最小二乘法。
应该是重定向错误了，确实不是同一个，俺顺手改了
讲的不是很通俗易懂 可以结合图来说明最小二乘法的用法呵