标准误差
出自 MBA智库百科(https://wiki.mbalib.com/)
标准误差(Standard error),也称均方根误差(Root mean squared error)
目录 |
标准误差是指在抽样试验(或重复的等精度测量)中,常用到样本平均数的标准差。注意:标准差与标准误差是两个不同的概念[1]。
标准误差是当前应用最广泛、最基本的一种随机误差的表示方法,当标准误差求得后,平均误差和极限差即可求得 故国际上普遍采用标准误差作为实验结果质量的数字指标,同时按国际计量局建议,不确定度用标准差σ表征(或方差σ2表征)。由此可知,标准误差在数据处理上的作用十分重要[2]。
设n个测量值的误差为E1、E2……En,则这组测量值的标准差σ等于:
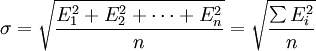
其中,E = Xi − T,式中:E-误差;Xi-测定值;T-真实值。
由于被测量的真值是未知数,各测量值的误差也都不知道,因此不能按上式求得标准误差。测量时能够得到的是算术平均值,它最接近真值(N),而且也容易算出测量值和算术平均值之差,称为残差(记为v)。理论分析表明可以用残差v表示有限次(n次)观测中的某一次测量结果的标准差σ,其计算公式为:
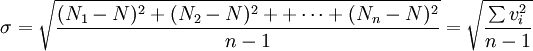
对于一组等精度测量(n次测量)数据的算术平均值,其误差应该更小些。理论分析表明,它的算术平均值的标准误差。有的书中或计算器上用符号s表示):
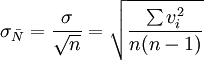
需要注意的是,标准误差不是测量值的实际误差,也不是误差范围,它只是对一组测量数据可靠性的估计。标准误差小,测量的可靠性大一些,反之,测量就不大可靠。进一步的分析表明,根据偶然误差的高斯理论,当一组测量值的标准误差为σ时,则其中的任何一个测量值的误差Ei有68.3%的可能性是在(-σ,+σ)区间内。
世界上多数国家的物理实验和正式的科学实验报告都是用标准误差评价数据的,现在稍好一些的计算器都有计算标准误差的功能,因此,了解标准误差是必要的。
标准误与标准差的区别[1]
标准差与标准误的意义、作用和使用范围均不同。标准差(亦称单数标准差)一般用s表示,是表示个体间变异大小的指标,反映了整个样本对样本平均数的离散程度,是数据精密度的衡量指标;而标准误一般用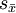 表示,反映样本平均数对总体平均数的变异程度,从而反映抽样误差的大小,是量度结果精密度的指标。
表示,反映样本平均数对总体平均数的变异程度,从而反映抽样误差的大小,是量度结果精密度的指标。
随着样本数(或测量次数)n的增大,标准差趋向某个稳定值,即样本标准差s越接近总体标准差σ,而标准误则随着样本数(或测量次数)n的增大逐渐减小,即样本平均数越接近总体平均数μ;故在实验中也经常采用适当增加样本数(或测量次数)n减小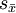 的方法来减小实验误差,但样本数太大意义也不大。标准差是最常用的统计量,一般用于表示一组样本变量的分散程度;标准误一般用于统计推断中,主要包括假设检验和参数估计,如样本平均数的假设检验、参数的区间估计与点估计等。
的方法来减小实验误差,但样本数太大意义也不大。标准差是最常用的统计量,一般用于表示一组样本变量的分散程度;标准误一般用于统计推断中,主要包括假设检验和参数估计,如样本平均数的假设检验、参数的区间估计与点估计等。
标准差与标准误既有明显区别,又密切相关:标准误是标准差的1/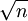 ;二者都是衡量样本变量(观测值)随机性的指标,只是从不同角度来反映误差;二者在统计推断和误差分析中都有重要的应用。
;二者都是衡量样本变量(观测值)随机性的指标,只是从不同角度来反映误差;二者在统计推断和误差分析中都有重要的应用。








这是标准差standard variation而不是standard error