点估计
出自 MBA智库百科(https://wiki.mbalib.com/)
点估计(Point estimation)
目录 |
点估计也称定值估计,它是以抽样得到的样本指标作为总体指标的估计量,并以样本指标的实际值直接作为总体未知参数的估计值的一种推断方法。
点估计的方法有矩估计法、顺序统计量法、最大似然法、最小二乘法等。这里仅介绍最为简单、直观又常用的矩估计法。
在统计学中,矩是指以期望为基础而定义的数字特征,一般分为原点矩和中心矩。
设X为随机变量,对任意正整数k,称E(Xk)为随机变量X的k阶原点矩,记为:
- mk = E(Xk)
- 当k=1时,
- m1 = E(X) = μ
可见一阶原点矩为随机变量X的数学期望。
我们把Ck = E[X − E(X)]k称为以E(X)为中心的k阶中心矩。
显然,当k=2时,
C2 = E[X − E(X)]2 = σ2
可见二阶中心矩为随机变量X的方差。
例1:已知某种灯泡的寿命X~N(μ,σ2),其中,μ,σ2都是未知的,今随机取得4只灯泡,测得寿命(单位:小时)为1502,1453,1367,1650,试估计μ和σ。
解:因为μ是全体灯泡的平均寿命, 为样本的平均寿命,很自然地会想到用
为样本的平均寿命,很自然地会想到用 去估计μ;同理用S去估计 。由于
去估计μ;同理用S去估计 。由于
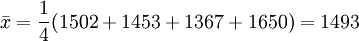
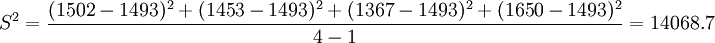
- S=118.61
故μ及σ的估计值分别为1493小时及118.61小时。
矩估计法简便、直观,比较常用,但是矩估计法也有其局限性。首先,它要求总体的k阶原点矩存在,若不存在则无法估计;其次,矩估计法不能充分地利用估计时已掌握的有关总体分布形式的信息。
通常设θ为总体X的待估计参数,一般用样本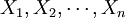 构成一个统计量
构成一个统计量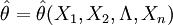 来估计θ则称
来估计θ则称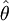 为θ的估计量。对于样本的一组数值
为θ的估计量。对于样本的一组数值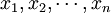 ,估计量
,估计量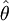 的值
的值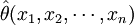 称θ的估计值。于是点估计即是寻求一个作为待估计参数θ的估计量
称θ的估计值。于是点估计即是寻求一个作为待估计参数θ的估计量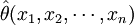 的问题。但是必须注意,对于样本的不同数值,估计值是不相同的。
的问题。但是必须注意,对于样本的不同数值,估计值是不相同的。
如在例中,我们分别用样本平均数和样本修正方差来估计总体数学期望和总体均方差,即有:
其对应于给定的估计值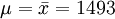 小时,
小时,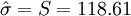 小时。[1]
小时。[1]
样本统计量,如样本均值 ,样本标准差S,样本成数如何用于对相应总体参数μ、σ和p的点估计值。直观上,这些样本统计量对相应总体参数的点估计值是很有吸引力的。然而,在用一个样本统计量作为点估计量之前,统计学应检验说明这些样本统计量是否具有某些与好的点估计量相联系的性质。本节我们讨论好的点估计量的性质:无偏性、有效性和一致性。
由于有许多不同的样本统计量用作总体不同参数的点估计量,本节我们采用如下的一般记号。
- θ——所感兴趣的总体参数
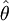 ——样本统计量或θ的点估计量
——样本统计量或θ的点估计量
θ代表一总体的参数,如总体均值、总体标准差和总体比率等等;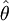 代表相应的样本统计量,如样本均值、样本标准差和样本比率。
代表相应的样本统计量,如样本均值、样本标准差和样本比率。
1、无偏性
如果样本统计量的数学期望等于所估计的总体参数的值,该样本统计量称作总体参数的无偏估计量。无偏性的定义如下:
如果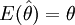
则称样本统计量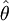 是总体参数θ的无偏估计。
是总体参数θ的无偏估计。
式中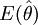 ——样本统计量
——样本统计量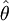 的数学期望
的数学期望
因此,样本无偏统计量的所有可能值的期望值或均值等于被估计的总体参数。
2、有效性
假定含n个元素的一个简单随机样本用于给出同一总体参数的两个不同的无偏点估计量。这时,我们偏好于用标准差较小的点估计量,因为它给出的估计值与总体参数更接近。有较小标准差的点估计量称作比其他点估计量有更好的相对效率。
3、一致性
与一个好的点估计相联系的第三个性质为一致性。粗略地讲,如果当样本容量更大时,点估计量的值更接近于总体参数,该点估计量是一致的。换言之,大样本比小样本趋于接进一个更好的点估计。注意到对样本均值 ,我们证明标准差
,我们证明标准差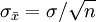 。由于
。由于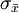 与样本容量相关,较大的样本容量得到的\sigma_{\bar{x}}的值更小,我们得出大样本容量趋于给出的点估计更接近于总体均值μ。在这个意义上,我们可以说样本均值是总体均值μ的一个一致估计量。
与样本容量相关,较大的样本容量得到的\sigma_{\bar{x}}的值更小,我们得出大样本容量趋于给出的点估计更接近于总体均值μ。在这个意义上,我们可以说样本均值是总体均值μ的一个一致估计量。
但由于在实际抽样调查中一次只是随机抽取一个样本,导致估计值会因样本的不同而不同,甚至产生很大的差异。所以说,点估计是一种的估计或推断,其缺点是既没有解决参数估计的精确问题,也没有考虑估计的可靠性程度,只有区间估计才能解决这两个问题。不过,由于点估计直观、简单,对于那些要求不太高的判断和分析,可以使用此种方法。
- ↑ 王淑珍,赵邦宏等.第四章 抽样推断 资产评估统计与预测.中国财政经济出版社,2001.第85页
评论(共9条)
例1中的总体样本标准差是不是计算错误啊!
例题是参考《资产评估统计与预测》的,在参考文献中有提示,您可以参考。
例1中的总体样本标准差是不是计算错误啊!
不是计算错误 是样本的方差计算与总体方差计算略有不同 总体是除以n 样本则是除以n-1
灯泡的那个问题,下面的分母应该是N,而不是N-1/。
有提供相关参考文献,您可以参考一下~
發問也要先思考一下吼
灯泡的那个问题,下面的分母应该是N,而不是N-1/。
no mistake, for population, we use N to calcilate, but for the sample, we use n-1 to get its sample variance
例1中的总体样本标准差是不是计算错误啊!
没有错误,自由度是n-1
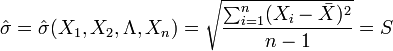








例1中的总体样本标准差是不是计算错误啊!