抽样指标
出自 MBA智库百科(https://wiki.mbalib.com/)
抽样指标(Sampling indicator)
目录 |
抽样指标又称“样本指标”、“样本统计量”,由样本总体各单位标志值计算出来反映样本特征,用来估计全及指标的综合指标。统计量是样本变量的函数,用来估计总体参数,因此与总体参数相对应,统计量有样本平均数(或抽样成数)、样本标准差(或样本方差 )。
对于一个问题全及总体是唯一确定的,所以全及指标也是唯一确定的,全及指标也称为参数,它是待估计的数。而统计量则是随机变量,它的取值随样本的不同而发生变化。
抽样指标是用来估计全及指标的,因此和全及指标相对应,有抽样平均数 ,抽样成数p,及样本标准差 σi,样本方差
,抽样成数p,及样本标准差 σi,样本方差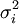 等等。
等等。
1、样本平均数及样本方差(样本标准差)。
设样本有n个变量:x1、x2、…、xn。则抽样平均数为:
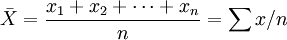
样本方差: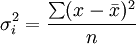
样本标准差: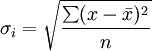
2、样本成数及样本成数标准差。
设样本n个单位中有n1个单位具有某种属性,n0 个单位不具有某种属性,n1 + n2 = n,p为样本中具有某种属性的单位数所占的比重,q为不具有某种属性的单位数所占的比重,则抽样成数为:
p = n1 / n q = n0 / n = (n − n1) / n = 1 − p
同理,样本成数标准差为:
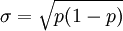








为什么样本方差不是除以n-1??