點估計
出自 MBA智库百科(https://wiki.mbalib.com/)
點估計(Point estimation)
目錄 |
點估計也稱定值估計,它是以抽樣得到的樣本指標作為總體指標的估計量,並以樣本指標的實際值直接作為總體未知參數的估計值的一種推斷方法。
點估計的方法有矩估計法、順序統計量法、最大似然法、最小二乘法等。這裡僅介紹最為簡單、直觀又常用的矩估計法。
在統計學中,矩是指以期望為基礎而定義的數字特征,一般分為原點矩和中心矩。
設X為隨機變數,對任意正整數k,稱E(Xk)為隨機變數X的k階原點矩,記為:
- mk = E(Xk)
- 當k=1時,
- m1 = E(X) = μ
可見一階原點矩為隨機變數X的數學期望。
我們把Ck = E[X − E(X)]k稱為以E(X)為中心的k階中心矩。
顯然,當k=2時,
C2 = E[X − E(X)]2 = σ2
可見二階中心矩為隨機變數X的方差。
例1:已知某種燈泡的壽命X~N(μ,σ2),其中,μ,σ2都是未知的,今隨機取得4只燈泡,測得壽命(單位:小時)為1502,1453,1367,1650,試估計μ和σ。
解:因為μ是全體燈泡的平均壽命, 為樣本的平均壽命,很自然地會想到用
為樣本的平均壽命,很自然地會想到用 去估計μ;同理用S去估計 。由於
去估計μ;同理用S去估計 。由於
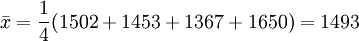
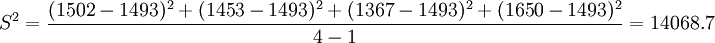
- S=118.61
故μ及σ的估計值分別為1493小時及118.61小時。
矩估計法簡便、直觀,比較常用,但是矩估計法也有其局限性。首先,它要求總體的k階原點矩存在,若不存在則無法估計;其次,矩估計法不能充分地利用估計時已掌握的有關總體分佈形式的信息。
通常設θ為總體X的待估計參數,一般用樣本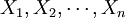 構成一個統計量
構成一個統計量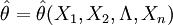 來估計θ則稱
來估計θ則稱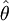 為θ的估計量。對於樣本的一組數值
為θ的估計量。對於樣本的一組數值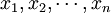 ,估計量
,估計量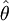 的值
的值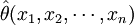 稱θ的估計值。於是點估計即是尋求一個作為待估計參數θ的估計量
稱θ的估計值。於是點估計即是尋求一個作為待估計參數θ的估計量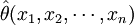 的問題。但是必須註意,對於樣本的不同數值,估計值是不相同的。
的問題。但是必須註意,對於樣本的不同數值,估計值是不相同的。
如在例中,我們分別用樣本平均數和樣本修正方差來估計總體數學期望和總體均方差,即有:
其對應於給定的估計值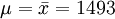 小時,
小時,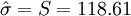 小時。[1]
小時。[1]
樣本統計量,如樣本均值 ,樣本標準差S,樣本成數如何用於對相應總體參數μ、σ和p的點估計值。直觀上,這些樣本統計量對相應總體參數的點估計值是很有吸引力的。然而,在用一個樣本統計量作為點估計量之前,統計學應檢驗說明這些樣本統計量是否具有某些與好的點估計量相聯繫的性質。本節我們討論好的點估計量的性質:無偏性、有效性和一致性。
由於有許多不同的樣本統計量用作總體不同參數的點估計量,本節我們採用如下的一般記號。
- θ——所感興趣的總體參數
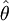 ——樣本統計量或θ的點估計量
——樣本統計量或θ的點估計量
θ代表一總體的參數,如總體均值、總體標準差和總體比率等等;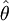 代表相應的樣本統計量,如樣本均值、樣本標準差和樣本比率。
代表相應的樣本統計量,如樣本均值、樣本標準差和樣本比率。
1、無偏性
如果樣本統計量的數學期望等於所估計的總體參數的值,該樣本統計量稱作總體參數的無偏估計量。無偏性的定義如下:
如果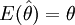
則稱樣本統計量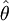 是總體參數θ的無偏估計。
是總體參數θ的無偏估計。
式中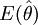 ——樣本統計量
——樣本統計量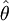 的數學期望
的數學期望
因此,樣本無偏統計量的所有可能值的期望值或均值等於被估計的總體參數。
2、有效性
假定含n個元素的一個簡單隨機樣本用於給出同一總體參數的兩個不同的無偏點估計量。這時,我們偏好於用標準差較小的點估計量,因為它給出的估計值與總體參數更接近。有較小標準差的點估計量稱作比其他點估計量有更好的相對效率。
3、一致性
與一個好的點估計相聯繫的第三個性質為一致性。粗略地講,如果當樣本容量更大時,點估計量的值更接近於總體參數,該點估計量是一致的。換言之,大樣本比小樣本趨於接進一個更好的點估計。註意到對樣本均值 ,我們證明標準差
,我們證明標準差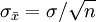 。由於
。由於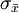 與樣本容量相關,較大的樣本容量得到的\sigma_{\bar{x}}的值更小,我們得出大樣本容量趨於給出的點估計更接近於總體均值μ。在這個意義上,我們可以說樣本均值是總體均值μ的一個一致估計量。
與樣本容量相關,較大的樣本容量得到的\sigma_{\bar{x}}的值更小,我們得出大樣本容量趨於給出的點估計更接近於總體均值μ。在這個意義上,我們可以說樣本均值是總體均值μ的一個一致估計量。
但由於在實際抽樣調查中一次只是隨機抽取一個樣本,導致估計值會因樣本的不同而不同,甚至產生很大的差異。所以說,點估計是一種的估計或推斷,其缺點是既沒有解決參數估計的精確問題,也沒有考慮估計的可靠性程度,只有區間估計才能解決這兩個問題。不過,由於點估計直觀、簡單,對於那些要求不太高的判斷和分析,可以使用此種方法。
- ↑ 王淑珍,趙邦巨集等.第四章 抽樣推斷 資產評估統計與預測.中國財政經濟出版社,2001.第85頁
評論(共9條)
例1中的總體樣本標準差是不是計算錯誤啊!
例題是參考《資產評估統計與預測》的,在參考文獻中有提示,您可以參考。
例1中的總體樣本標準差是不是計算錯誤啊!
不是計算錯誤 是樣本的方差計算與總體方差計算略有不同 總體是除以n 樣本則是除以n-1
燈泡的那個問題,下麵的分母應該是N,而不是N-1/。
有提供相關參考文獻,您可以參考一下~
發問也要先思考一下吼
燈泡的那個問題,下麵的分母應該是N,而不是N-1/。
no mistake, for population, we use N to calcilate, but for the sample, we use n-1 to get its sample variance
例1中的總體樣本標準差是不是計算錯誤啊!
沒有錯誤,自由度是n-1
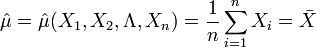
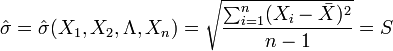








例1中的總體樣本標準差是不是計算錯誤啊!