順序統計量法
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
定義:設 是總體ζ的樣本,將其按大小排列為
是總體ζ的樣本,將其按大小排列為
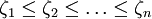
稱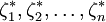 為順序統計量。
為順序統計量。
明顯地,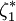 與
與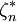 分別是樣本
分別是樣本 的最小值與最大值。稱
的最小值與最大值。稱
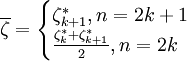
為樣本中位數。
樣本中位數的取值規則是:將樣本值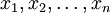 從小至大排成
從小至大排成
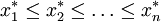
當n=2k+1時,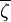 取居中的數據
取居中的數據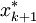 為其觀測值;當n=2k時,
為其觀測值;當n=2k時,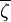 取居中的兩個數據的平均值
取居中的兩個數據的平均值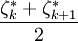 為其觀測值.中位數
為其觀測值.中位數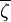 帶來了總體ζ取值的平均數的信息,因此用
帶來了總體ζ取值的平均數的信息,因此用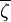 估計總體ζ的數學期望是合適的.
估計總體ζ的數學期望是合適的.
用樣本中位數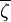 估計總體ζ的數學期望的方法稱數學期望的順序統計量估計法.
估計總體ζ的數學期望的方法稱數學期望的順序統計量估計法.
順序統計量估計法的優點是計算簡便,且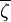 不易受個別異常數據的影響.如果一組樣本值某一數據異常(如過於小或過於大),則這個異常數據可能是總體ζ的隨機性造成的,也可能是受外來干擾造成的(如工作人員粗心,記錄錯誤),當原因屬於後者,用樣本平均值
不易受個別異常數據的影響.如果一組樣本值某一數據異常(如過於小或過於大),則這個異常數據可能是總體ζ的隨機性造成的,也可能是受外來干擾造成的(如工作人員粗心,記錄錯誤),當原因屬於後者,用樣本平均值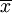 估計E(x)顯然受到影響,但用樣本中位數
估計E(x)顯然受到影響,但用樣本中位數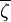 估計E(x)時,由於一個(甚至幾個)異常的數據不易改變中位數眚取值,所以估計值不易受到影響.
估計E(x)時,由於一個(甚至幾個)異常的數據不易改變中位數眚取值,所以估計值不易受到影響.
即稱R=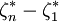 為樣本極差.
為樣本極差.
由於樣本極差帶來總體眚取值離散程度的信息,因此可以用R作為對總體ζ的標準差σ的估計(R與σ量綱相同).用樣本極差對總體ζ的標準差作估計的方法稱為極差估計法.
極差估計法的優點是計算簡便,但不如用S可靠,n越大兩者可靠的程度差別越大,這時一般不用極差估計







