顺序统计量法
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
定义:设 是总体ζ的样本,将其按大小排列为
是总体ζ的样本,将其按大小排列为
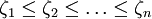
称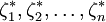 为顺序统计量。
为顺序统计量。
明显地,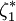 与
与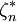 分别是样本
分别是样本 的最小值与最大值。称
的最小值与最大值。称
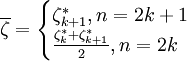
为样本中位数。
样本中位数的取值规则是:将样本值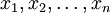 从小至大排成
从小至大排成
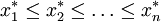
当n=2k+1时,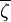 取居中的数据
取居中的数据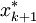 为其观测值;当n=2k时,
为其观测值;当n=2k时,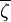 取居中的两个数据的平均值
取居中的两个数据的平均值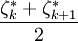 为其观测值.中位数
为其观测值.中位数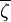 带来了总体ζ取值的平均数的信息,因此用
带来了总体ζ取值的平均数的信息,因此用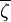 估计总体ζ的数学期望是合适的.
估计总体ζ的数学期望是合适的.
用样本中位数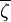 估计总体ζ的数学期望的方法称数学期望的顺序统计量估计法.
估计总体ζ的数学期望的方法称数学期望的顺序统计量估计法.
顺序统计量估计法的优点是计算简便,且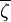 不易受个别异常数据的影响.如果一组样本值某一数据异常(如过于小或过于大),则这个异常数据可能是总体ζ的随机性造成的,也可能是受外来干扰造成的(如工作人员粗心,记录错误),当原因属于后者,用样本平均值
不易受个别异常数据的影响.如果一组样本值某一数据异常(如过于小或过于大),则这个异常数据可能是总体ζ的随机性造成的,也可能是受外来干扰造成的(如工作人员粗心,记录错误),当原因属于后者,用样本平均值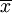 估计E(x)显然受到影响,但用样本中位数
估计E(x)显然受到影响,但用样本中位数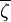 估计E(x)时,由于一个(甚至几个)异常的数据不易改变中位数眚取值,所以估计值不易受到影响.
估计E(x)时,由于一个(甚至几个)异常的数据不易改变中位数眚取值,所以估计值不易受到影响.
即称R=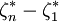 为样本极差.
为样本极差.
由于样本极差带来总体眚取值离散程度的信息,因此可以用R作为对总体ζ的标准差σ的估计(R与σ量纲相同).用样本极差对总体ζ的标准差作估计的方法称为极差估计法.
极差估计法的优点是计算简便,但不如用S可靠,n越大两者可靠的程度差别越大,这时一般不用极差估计







