質量屋
出自 MBA智库百科(https://wiki.mbalib.com/)
質量屋(the House of Quality)
目錄 |
質量屋是由美國學者J.R.Hauser與D.C1ausing於1988年提出。“質量屋”是質量功能配置(QFD)的核心。
質量屋是一種確定顧客需求和相應產品或服務性能之間聯繫的圖示方法。
質量屋(the House of Quality)一直是產品開發中連接用戶需求與產品屬性的經典工具。例如在一個相機產品開中,市場研究得到了用戶對產品的若幹需求,如,質量輕、使用方便、可靠、容易拿穩等等。通過市場人員與設計人員共同工作,確定實現不同需求可行的方式。這個過程同時排除掉了一些目前技術無法實現的需求,就像選擇傢具。一個完整的質量屋,還包括競爭對手表現、技術指標之間的關係、技術指標重要性得分等信息。
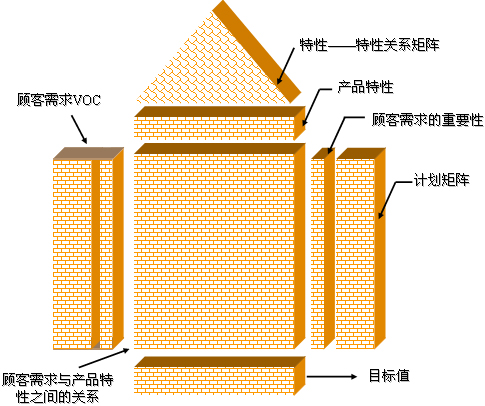
圖1 質量屋圖示
質量屋雖然是一個經典工具,但也只是一個基礎工具,對複雜產品設計體系仍有局限。例如,該工具對於住宅產品來說並不是一個完美的工具。因為住宅產品不是一個簡單屬性的疊加,而是一個綜合的解決方案。人們對房屋產品的整體的需求感受,驅動著人們對房屋各空間需求及其權衡取捨。這樣,在住宅需求與住宅產品之間包含兩層映射關係,一方面是整體的映射,另一方面是每個空間屬性之間的映射。
以用戶為中心的產品開發,建立在利用專業研究技術探求消費者心靈深處需求的基礎上。這種需求是高度凝煉的,是一定時期內產品需要的原始驅動力。如果說研究用戶的消費需求是對飄散的心靈電波的捕捉,建立營銷語言和設計語言之間有效的對接,才能破譯消費者心靈深處的密碼,從而最終使需求信息在產品開發中發揮真正作用。
質量屋是一種直觀的矩陣框架表達形式,是QFD方法的工具。建立質量屋的基本框架,給以輸入信息,通過分析評價得到輸出信息,從而實現一種需求轉換。通常的質量屋如圖1所示,其由以下幾個廣義矩陣部分組成:WHATS矩陣,表示需求什麼;HOWS矩陣,表示針對需求怎樣雲做;相關關係矩陣,表示WHATS項的相關關係;HOWS的相互關係矩陣,表示HOWS陣內各項目的關聯關係;評價矩陣,表示HOWS項的組織度或技術成本評價情況;競爭性或可競爭力或可行性分析比較。質量屋建立完成後,通過定性和定量分析得到輸出項——HOWS項,即完成了“需求什麼”到“怎樣去做”的轉換。
質量屋(HOQ)是驅動整個QFD(質量功能展開)過程的核心,它是一個大型的矩陣,由7個不同的部分組成(圖1)。這7個組成部分分別是:
(1)顧客需求(customer requirements)。即VOC,通常它們可用親密度圖和樹圖表示。不同的產品有不同的顧客需求。例如,對於汽車來說,顧客需求可能是車門容易開啟;對於銀行來說,顧客需求可能是取款不用排隊等。QFD就是用來部署(deploy)VOC的,而不是用來收集VOC的。收集VOC則是另一個相對獨立的過程。
(2)產品特性(product features)。它們也可以用親密度圖和樹圖表示。產品特性是我們用以滿足顧客需求的手段,產品特性也因產品不同而有差異。如對於車門,產品特性可能是關門所需的力量;對於割草機,產品特性可能是轉動軸所需的推力。產品特性必須用標準化的表述。QFD中是利用顧客需求來產生產品特性的。
(3)顧客需求的重要性(importance of customer requirements)。我們不僅需要知道顧客需求些什麼,還要知道這些需求對於顧客的重要程度。
(4)計劃矩陣(planning matrix)。該矩陣包含一個對主要競爭對手產品的競爭性分析。矩陣中包括3列,分別代表對於現有產品所需的改進(改進率)、改進後可能增加的銷售量(銷售點)以及每個顧客需求的得分。
(5)顧客需求與產品特性之間的關係。這是矩陣的本體(中間部分),表示產品特性對各個顧客需求的貢獻和影響程度。
(6)特性與特性之間的關係。一般地,一個特性的改變往往影響另一個特性。通常這種影響是負向的,即一個特性的改進往往導致另一個特性變壞。該特性關係圖使我們能辨別這些特性之間的影響,以求得折衷方案。
工程一一般的產品開發過程包括規劃階段、綜合設計階段、工藝階段和生產計劃階段。在應用QFD方法時要先建立各階段的質量屋,再進行需求變換,最後形成明確的生產要求,從而完成產品開發的質量功能配置的全過程。
QFD是一個跨專業的團隊過程;
QFD是一種思想,一種產品開發和質量保證的方法論。它要求我們產品開發直接面向顧客需求,在產品設計階段考慮工藝和製造問題,而質量屋則是在產品開發中具體實現這種方法論的工具 ;
QFD是一個非常結構化(structured)的、矩陣驅動(matrix-driven)的過程,其運行包括4個階段:
- 將顧客需求(customer requirements)轉化產品特性(performance measures)
- 將產品特性轉化成零件特性(features and technology)
- 將零件特性轉化成關鍵工藝操作(parts specification)
- 將關鍵工藝操作轉化成生產要求(manufacturing processes)。
以下對各階段質量屋的建立作論述以便於對質量屋概念的理解和對QFD系統的認識。
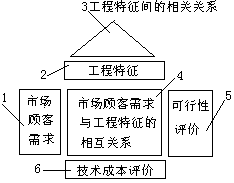
(1)產品規劃階段的質量屋 產品規劃階段的質量屋的構成形式如圖2所示,其由下述幾個部分組成。
圖2 產品規劃階段的質量屋
第一部分是一個若幹行一列的列陣,此列陣所反映的內容是市場顧客對產品的各種需求,(WHATS項)。這些市場顧客需求是通過對市場和顧客的需求將按過程驅動產品的QFD過程展開。市場顧客的需求是各種各樣的,此項矩陣的建立應儘量充分、準確和合理,否則後續的所有需求變換工作者可能相對於真實的市場顧客需求而失真。就顧客的要求而言,亦有主次、輕重之分,QFD方法中對此的處理是:對市場顧客的各項需求給以權重因數以便進行排序,定義權重因數的總和為100%。註意,這裡有顧客對象的權重區分,例如有主要客戶對象和一般客戶對象之分,顯然不同客戶需求的重要程度是不同的。也有同類市場顧客對產品的諸多質量功能要求排序時要註意避免重大的疏漏,亦要避免產品的冗餘功能。這不工作是QFD實施成功的關鍵。
第二部分是一個一行若幹列的行矩陣,是用來描述對應於市場顧客需求的工程特征要求,即有什麼樣的市場顧客需求就應有什麼樣的工程特征要求來對應保證。這種對應是多相關性的,市場顧客的某種需求可能對應著若幹項工程特征要求,若幹種工程特征要求有機結合才能滿足某種市場顧客需求項。反過來講,某種工程特征也可以同時滿足若幹項市場顧客的需求。工程特征要求是市場顧客需求的映射變換結果。
在以下論述中將會看到,這一階段的工程特征要求將作為下一階段質量屋的WHATS項。
第三部分稱為質量屋的屋頂,在數學上是一個三角形矩陣,它表示的是工程特征之間的相關關係。從辯證法的觀點來看,實現一個產品的諸多質量功能需求對應著諸多工程特征,各種市場顧客的質量功能需求之間有著相互關聯影響,從而各種工程特征之間亦有著相互關聯影響,某一種工程特征的改變會影響到其它工程特征跟著變化。為簡化問題起見,在QFD技術中以三種形式來定性地描述工程特征之間的相關影響關係,即正相關(向相同方向變化)、不相關和負相關(向相反方向變化)。對相關程度還可以進一步地細分為強相關、一般相關和弱相關幾種關係,並給以標度值來表達相關程度。據此可以對工程特征進行分析研究,發現各種工程特征之間可能存在的矛盾,由此重新進行設計,避免矛盾的產生。
第四部分是一個關係矩陣,該矩陣的行數與第一部分相同,列數與第二部分相同。表示各個工程特征項與各個幣場顧客需求項的相互關係。各個項之間的錯綜複雜關係可以定量地給以分值來表示。一般分:強相關給九分,可理解成為了滿足某種市揚顧客需求必需具備某種工程特征要求;一般相關給三分,可理解成為了滿足某種市場顧客需求可以採用不同的工程特征與之對應;弱相關給一分,表示兩項之間的關聯關係很弱。利用關係矩陣可以明確工程特征與市場顧客需求間的對應關係。
第五部分是一個產品可行性評價矩陣,又稱為市場評估矩陣,其行數與市場顧客需求矩陣相同,列數可以是一列,其中的內容表示要開發的產品針對各項市場顧客需求的競爭能力估價值。同時引人若幹個市場上同類產品作為競爭對象進行比較,以判斷產品的市場競爭力,由此在產品開發初期找出不足之處以進行調整改進。 第六部分是產品規劃階段的技術和成本評估矩陣,其行列數與工程特征矩陣相對應,其中要建立的內容是各項工程特征的技術和成本評價數據,同時也建立若幹個同類產品的相對應的數據信息進行分析對比,找出不足之處,提出改進措施。
這六個部分的矩陣構造完成後便形成了產品規劃階段的質量屋,這個質量屋的基本輸入是市場顧客需求,針對需求的對策是一組工程特征需求,從而進行了需求變換。通過變換將市場顧客對產品的相對離散和模糊的需求變換為明確的工程特征要求。
在這一過程中會不可避免地產生各種矛盾衝突。例如有市場顧客對產品的各種要求的衝突,如質量和成本的衝突,功能間的衝突等;有工程特征間技術上的矛盾關係;還有與同類產品對比而產生的競爭力和技術成本的不協調問題等等。這些矛盾衝突是需要解決的,決定產品規劃階段質量屋的輸出工作就是利用質量屋這種形式化的工具進行迭代分析來解決上述的矛盾衝突。對複雜的問題可以採用電腦輔助QFD過程。產品規劃階段質量屋的最終輸出是工程特征要求列陣,通過實現工程特征要求來保證市場顧客的需求。
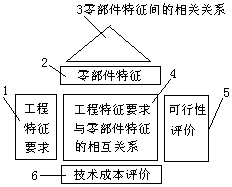
(2)零部件設計階段的質量屋 工程特征需求的實現是由綜合設計來保證的,在QFD方法中則還要建立體現綜合設計內容的零部件設計階段的質量屋。 該階段質量屋的構成形式與產品規劃階段的質量屋是類同的,如圖3所示。
圖3 零部件設計階段的質量屋
此階段質量屬的輸入項(WHATS項)是產品的工程特征要求列陣(卜一階段質量侵中力行矩陣,此處表示成列陣形式)。實現工程特征要求的對策是若幹項零部件特征(HOWS項),以矩陣2來表示。矩陣3表示的是各種零部件特征間的相關性。同樣,在工程特征要求矩陣和零部件特征矩陣之間存在的關係矩陣4表示相互關係。矩陣5是可行性評價矩陣,表示零部件特征對應於工程特征要求的可行性評價。矩陣6是技術評價矩陣,針對各項零部件特征進行技術和成本分析。
通過零部件設計階段的質量屋的建立和分析,可以找出實現工程特征要求的難點和薄弱環節,重新進行有關零部件特征的方案設計。
零部件設計階段的質量屋的最終輸出是能保證實現工程特征要求的零部件特征要求。
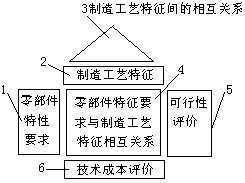
(3)工藝規劃階段的質量屋產品的零部件特征要求明確後,可以據此進行零部件的詳細設計。為實現零部件特征要求,則要進行工藝規劃設計,在QFD方法進程中對應的是工藝規劃階段質量屋的建立。該階段的質量屋的內容如圖4所示,質量屋的輸入是零部件特征要求(質量屋的WHATS項)。輸出是製造工藝特征要求(HOWS項)。通過這一過程完成產品的零部件設計要求向工藝流程設計的轉換。
圖4 工藝規劃階段的質量屋
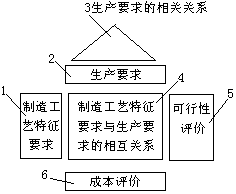
(4)生產計劃階段的質量屋工藝規劃階段質量屋的輸出是製造工藝特征要求。為滿足這些要求,要有生產計劃安排以形成明確的生產要求。對應地建立QFD的生產計劃階段的質量屋,其形式如圖5所示。此階段質量屋的輸入是產品的製造工藝特征要求,為實現製造工藝特征要求則要有明確的生產計劃安排,在生產計劃安排中包含諸多的生產要求。按這些要求就可以去組織產品的具體生產了。生產計劃階段質量屋的輸出就是生產要求信息。
圖5 生產計劃階段的質量屋
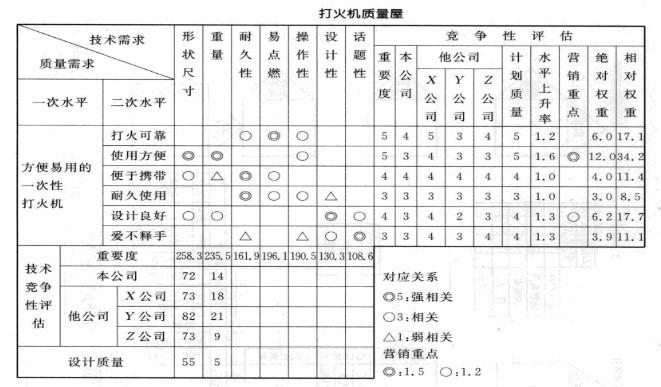
案例一:打火機質量屋實例[1]
打火機是吸煙人士隨身必帶的物品之一。雖然昂貴.做工考究的名牌打火機因為體現出了一個人的身份和品味而備受青睞。但是方便易用的一次性打火機也因為其便宜.式樣繁多的特性而受到人們的歡迎。然而。生產一次性打火機卻面臨很多問題。比如人們一般要求一次性打火機耐用(至少用光氣體前不會壞);在任何環境下都容易點著;最好樣式也多一些。能夠引起別人的註意。但具體生產的時候。一來不清楚各個顧客要求和生產有什麼聯繫。二來各個指標的權重分配也成問題。因此。在進行一次性打火機的設計和生產過程里。使用了以質量屋矩陣為核心的QFD。最終。顧客的需求轉變成產品的技術特性。併在生產過程中得到很好的支撐。
本例中。我們詳細描述瞭如何構造打火機的質量屋。
- (1)顧客需求
①顧客需求的獲取
能否及時地獲取顧客需求即顧客的聲音(Voice 0f Customer,VOC)以及所獲取的顧客需求是否全面、詳盡、真實。是成功實施和應用QFD的基礎。我們必須科學地選擇所要調查的對象.調查的方法以及後面的分析方法。這樣,在調查完成之後。我們才能最忠實地保持顧客聲音的原貌。
對於一次性打火機的用戶資料的收集。首先。我們考慮到一次性打火機的使用者(吸煙人士)一般都是中青年的男性。也就是15~35歲的男子。這個階段的男子考慮打火機的方便使用,款式時尚、更換容易、價格低廉等特性的多些。因此是一次性打火機的主要消費者。那麼調查的時候。就要儘可能的在這個年齡範圍內進行。至於職業.地域分佈倒是可以考慮的少些。
另外。在進行調查的時候。考慮到地域可能分佈較廣。可以採用郵寄問卷的方法。雖然該方法可能回收期長些。回收率也不是太高。但其低廉的費用還是比較適合大範圍的調查的。下表是設計的調查用表樣例。
通過以上的調查。將會得到很龐大的顧客需求的資料。由於調查對象的文字描述的模糊性和語言風格的特異性。有必要對上述資料進行整理和分析。提取出相同的元素或項目。
②顧客需求的分析和整理
收集到的顧客需求是各種各樣的。有要求.意見.抱怨.評價和希望。有關於質量的。有涉及功能的。還有涉及價格的。所以必須對從用戶那裡收集到的情報進行分類.整理。通過對調查信息的分析與整理。形成QFD配置所需的顧客需求信息及形式。一般我們通過下麵幾個步驟來實現這個轉化過程。
③概括合併顧客需求
顧客對其需求的描述經常很長。為了便於在QFD矩陣中輸入。必須對它們進行概括。在用簡潔明瞭的語言概括顧客需求後。應將表達同一含義或相似含義的顧客需求進行合併。一般來說。總顧客需求數目最好控制在25個以下。最多不要超過50個。
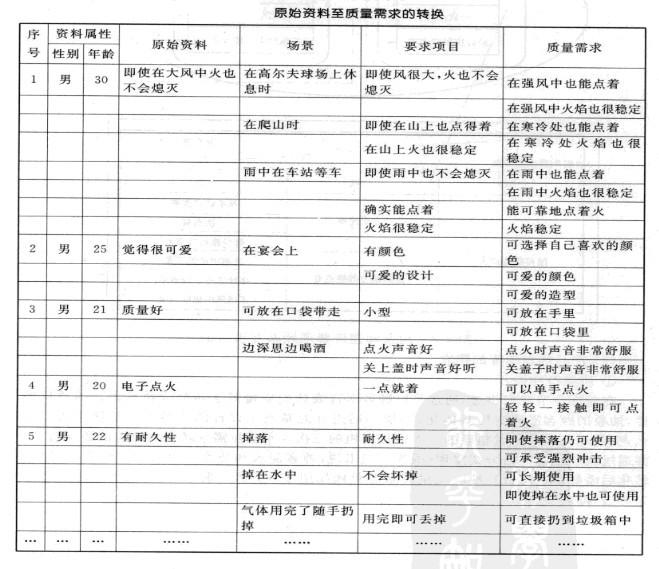
a.將原始資料變換成顧客的質量需求一般。先將原始資料變換成為要求項目。然後再將要求項目轉換為質量需求。註意在第一步變換中。最好能在不同的場景下考慮以便引出比較具體的要求項目。而在由要求項目向質量需求轉換時。要註意語言的簡潔.形象.具體和準確。每一項質量需求不要包含兩個以上方面的內容。
在本例中。我們將收集的資料進行適當排列。並針對每一個調查對象。進行一定的換位思考和場景聯想。力爭真正理解調查對象的需求。最後對得出的要求項目和質量需求進行整理。原始資料至質量需求的轉換如下表所示。
b.質量需求的分類與展開
上述整理後的顧客需求是隨意排列的。且存在重覆和條理性不強等問題。對它們合理的分類有助於QFD矩陣的方便構造。我們採用第三章講過的親和圖法對顧客需求進行分類。
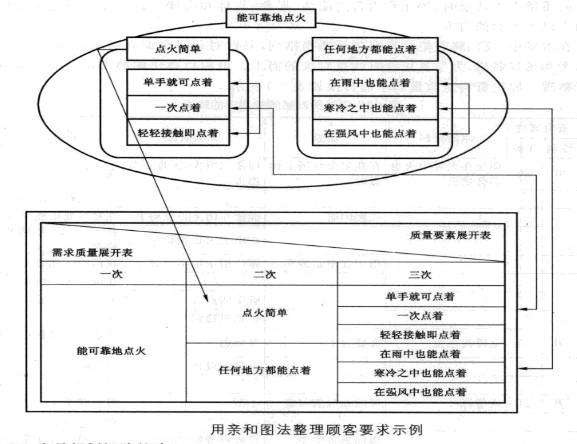
以“能可靠地點火”這一質量需求為例。列示了其中隱含的下層水平質量需求。用親和圖法整理顧客需求示例如圖4—8所示。
- (2)產品規劃矩陣的建立
①質量特性展開
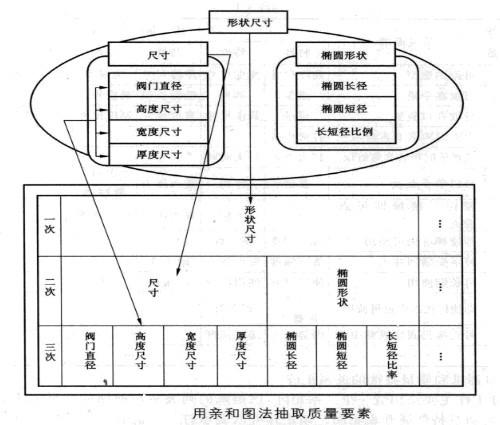
在前面章節我們講過。通過將以顧客語言表達的質量需求轉換成技術語言的質量特性。抽象的顧客需要變得具體化。並能夠通過在此基礎上設計的產品得以最終實現。那麼。我們也可以把經過整理的一次性打火機的三次水平質量需求轉化為對應的質量特性。並通過親和圖法進行分類整理(因為一般來說。顧客需求和技術需求之間存在著交叉性。轉化後需要整理綜合)。抽取質量要素的示例如下圖所示。最終。我們也可以得到一個矩陣表。即如下表。
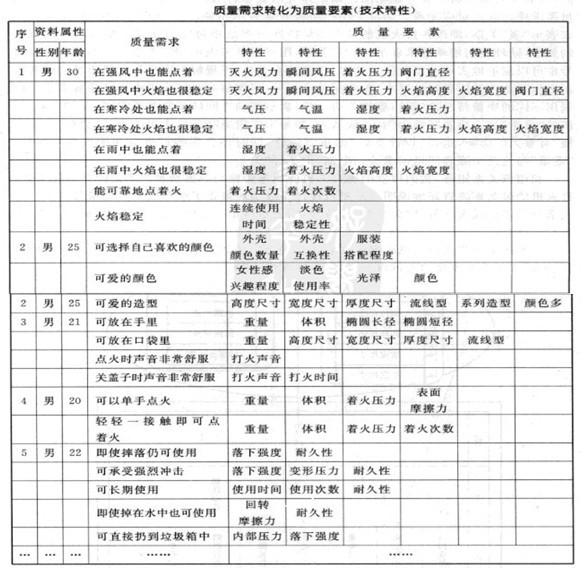
②質量需求和質量特性的關係矩陣
這部分工作主要是構造一個關係矩陣。該矩陣的列表頭與前面的質量需求展開表相同。行表頭與質量特性展開表相同。該矩陣可以表示打火機的各個質量特性項與各個質量需求項之間的對應關係。通常採用一組符號來表示相關程度的差異。例如。用雙圓圈來表示“強”關係。即改善打火機的某個質量特性與滿足相對應的顧客質量需求有比較強的關係。同理我們用單圓來表示“中等”關係。用三角形來表示“弱”關係。一組相關程度符號也可以定量地表示一組分值。這裡。強相關給五分。可理解為滿足打火機市場的顧客需求必須具備這種質量特性要求;中等相關給三分。可理解為對打火機市場的顧客需求可以採用不同的質量特性來滿足;弱相關給一分。表示兩項之間的關聯關係很弱。例如以打火機的“重量”這一質量特性為例。一般認為。如果採取措施降低打火機的重量。會對“使用方便”有重大的影響。也是“設計良好”的重要條件。同時還會影響打火機的便攜性。因此。“重量”與這兩個顧客質量需求分別呈強、中、弱的關係。
利用該關係矩陣。我們可以明確打火機的質量特性與顧客質量需求之間的對應關係。打火機的關係矩陣直觀地說明瞭質量特性是否適當地覆蓋了顧客需求。如果關係矩陣中關係符號很少或大部分是“關係微弱”符號。則表示質量特性沒有足夠地滿足顧客需求。應對它進行修改。
按上述步驟構造打火機質量屋如表4-11所示。在質量設計中。質量要素很多的情況下。可以選擇重要度高的進行重點設計。如本例中的“形狀尺寸”和“重量”。
案例二:基於質量屋矩陣的產品模塊劃分方法[2]
基於HOQ矩陣的兩階段分組方法,根據HOQ圖中的用戶需求與工程性能關係矩陣以及工程性能之間的互相關矩陣的不同特點,採用不同的分組策略,實現對用戶需求以及產品工程性能的分組,從而實現產品的模塊劃分以及對HOQ矩陣的分解。
- 1.用戶需求與工程性能的HOQ圖的建立
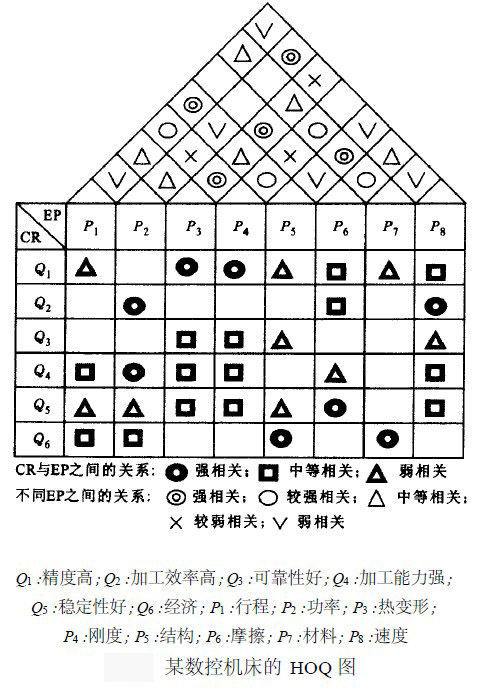
HOQ圖一般由7個部分組成,本文對其進行了簡化,僅對其中的用戶需求(CR)與工程性能(EP)的關係矩陣R,以及工程性能(EP)之間互相關矩陣C的組成進行討論.R中的關係繫數rij表示了用戶需求Qi與工程性能Pj之間關係的強度,若Qi與Pj之間沒有聯繫,則相應項保持空項,即表示rij = 0.相似地對於C,用互相關係數cij表示Pi與Pj之間關係的強度.目前,有多種確定rij和cij值的方法,如層次分析法(AHP)等.下圖所示是一個經過簡化的某機床用戶需求與工程性能的HOQ圖。
- 2.基於互相關矩陣的工程性能EP的分組
HOQ的EP互相關矩陣反映了工程性能彼此之間的耦合關係或約束關係,對EP分組就是在EP互相關矩陣的基礎上,將EP分解為彼此間具有緊密聯繫,而各組間具有較少耦合的幾組。可以採用元素間的距離d或元素的相似度s作為對元素分組的標準,並將距離較短或相似度較大的2個元素歸為一組.根據EP的互相關矩陣按以下方法得到EP的距離矩陣。
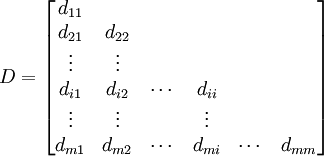
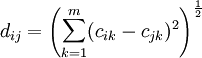 (
(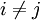 )
)
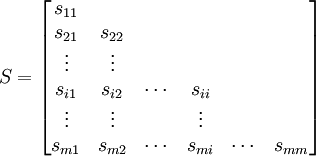
式中:dii = 0(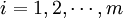 ).cik、cjk是EP互相關矩陣的元素,即Pk與Pi、Pj的互相關係數.由於D為一對稱矩陣,因此式中僅列出了其下三角的元素.由D可以得到EP的相似度矩陣。
).cik、cjk是EP互相關矩陣的元素,即Pk與Pi、Pj的互相關係數.由於D為一對稱矩陣,因此式中僅列出了其下三角的元素.由D可以得到EP的相似度矩陣。
 (
( )
)
式中:sij = max(sij)(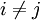 )。對EP的分組可採用傳統的層次分組演算法,如SL(Single Linkage)、AL(Average Linkage)、CL(Complete Linkage)等.MMC(Min-Max Cut)是Ding等所提出的一種用於圖像劃分和數據融合的方法,該方法可將圖像劃分問題轉換為對Fiedler特征值及其對應的特征向量的求解.本文將最大-最小(MMC)方法用於實現對EP的分組,在對EP分組時,必須遵守以下原則:①不同組之間元素的距離應儘可能大或它們的相似度應儘可能小;②同一組元素之間的距離應儘可能小或它們的相似度儘可能大.採用相似度作為EP分組的依據.假設有
)。對EP的分組可採用傳統的層次分組演算法,如SL(Single Linkage)、AL(Average Linkage)、CL(Complete Linkage)等.MMC(Min-Max Cut)是Ding等所提出的一種用於圖像劃分和數據融合的方法,該方法可將圖像劃分問題轉換為對Fiedler特征值及其對應的特征向量的求解.本文將最大-最小(MMC)方法用於實現對EP的分組,在對EP分組時,必須遵守以下原則:①不同組之間元素的距離應儘可能大或它們的相似度應儘可能小;②同一組元素之間的距離應儘可能小或它們的相似度儘可能大.採用相似度作為EP分組的依據.假設有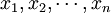 共n個元素,將其分為兩大組(C1和C2),則條件①為
共n個元素,將其分為兩大組(C1和C2),則條件①為
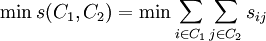
條件②為
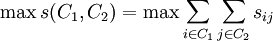
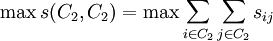
式中:sij是元素xi和xj的相似度.根據MMC方法,以上兩個條件可轉化為如下的目標函數。
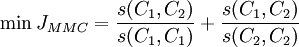 (1)
(1)
式(1)可通過下式求得最小值:
(W − S)q = λWq (2)
式中:W是一對角陣,其元素為| wii = | ∑ | sij |
| j |
 ,若某個分量qi > 0,則它所對應的項xi屬於C1組,否則xi屬於C2組.由此可將元素分為兩組,如果要繼續分組,可選擇其中一組作為分組對象,選擇的原則是具有最大平均距離的組,即使目標函數
,若某個分量qi > 0,則它所對應的項xi屬於C1組,否則xi屬於C2組.由此可將元素分為兩組,如果要繼續分組,可選擇其中一組作為分組對象,選擇的原則是具有最大平均距離的組,即使目標函數
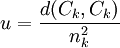
最大的Ck組為下一個分組對象,其中
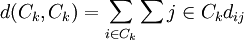
式中: nk是Ck中元素的個數. 再按max-min方法對其進行分組,由此可以得到多個分組方案.以平均損失度作為評判各分組方案優劣的依據,即
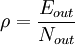
式中:Eout為C中位於各方塊陣外的所有相關係數cij之和;Nout為C中位於各方塊陣外所有單元的個數,即
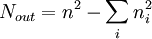
為使ρ為最小時所對應的分組情況為最優分組方
案,可將EP分為p組,分別為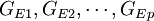 。
。
- 3.CR與EP的關係矩陣分解
對EP分組的基礎上, 按照以下2個原則對CR與EP的關係矩陣R進行分解:①惟一原則; ②滿意度最大原則. 原則①表示每個CR與EP只惟一地屬於某一模塊,原則②要求分解得到模塊的r元素總和為最大. 因此,首先將R轉化為CR與工程性能組GE的關係矩陣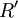 ,其元素
,其元素
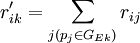
如下表所示,將對R的分解問題轉化為在同時滿足原則①和②的條件下,根據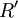 將CR劃分為p組的問題.
將CR劃分為p組的問題.
- 用戶需求與工程性能組的
 矩陣
矩陣
| 用戶需求 | 工程性能組 | |||||
|---|---|---|---|---|---|---|
| GE1 | GE2 |  | GEk |  | GEp | |
| Q1 | 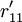 | 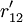 |  | 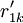 |  | 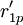
|
| Q2 | 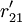 | 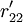 |  | 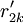 |  | 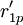
|
 |  |  |  | 
| ||
| Qi | 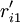 | 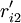 |  | 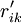 |  | 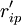
|
 |  |  |  | 
| ||
| Qm | 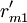 | 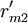 |  | 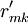 |  | 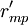
|
定義變數
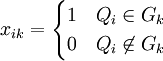 (3)
(3)
按照原則①,xik應滿足關係
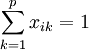 (
(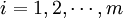 ) (4)
) (4)
提出目標函數
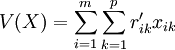 (5)
(5)
原則②可轉化為maxV(X),則對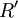 (即對R)的分解可轉換為在滿足約束式(3)、(4)的條件下,使式(5)最大化的優化問題,即一個帶約束的0-1整型優化問題.因此,可採用多種方法,如窮舉法、遺傳演算法等,來求解該優化問題。
(即對R)的分解可轉換為在滿足約束式(3)、(4)的條件下,使式(5)最大化的優化問題,即一個帶約束的0-1整型優化問題.因此,可採用多種方法,如窮舉法、遺傳演算法等,來求解該優化問題。
- 4.應用實例
以上圖所示的某數控機床的用戶需求與工程性能HOQ圖為例,用戶需求CR與工程性能EP之間的關係用弱(1),中等(3),強(9)來表示,工程性能EP之間的關係用弱(011),較弱(013),中等(015),較強(017),強(019)來表示.由此得到與EP有關的矩陣為。
C=
D=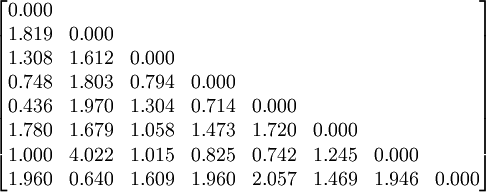
S=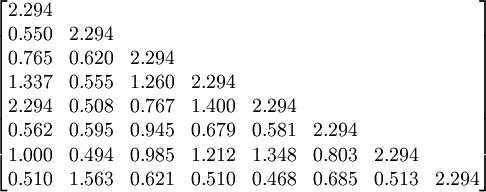
式(2)的次小特征值為01568,它所對應的特征向量(Fiedler向量)為(01285,-01596,010361,01212,01303,-01126,01195,-01609),因此可將EP分為GE1 = (P1,P3,P4,P5,P7),GE2 = (P2,P6,P8),Nout=30,ρ1 = 0.247。由於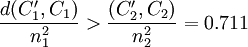
因此選擇P_2、P_6和P_8分為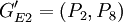 ,
,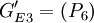 兩組,此時\Nout=3,ρ2 = 0.241。由於
兩組,此時\Nout=3,ρ2 = 0.241。由於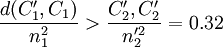 ,因此選擇P_1、P_3、P_4、P_5、和P_7、作為下一組分組對象,可分為G^\prime_{E1}=(P_1,P_5),
,因此選擇P_1、P_3、P_4、P_5、和P_7、作為下一組分組對象,可分為G^\prime_{E1}=(P_1,P_5),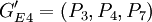 ,此時Nout=46,\rho_3=0.343.由於
,此時Nout=46,\rho_3=0.343.由於
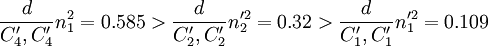 。
。
因此再次選擇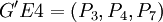 作為分組對象,可將其分為
作為分組對象,可將其分為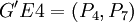 和
和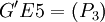 ,此時Nout=50,ρ4 = 0.372.由於ρ2最小,因此選擇它所對應的分組情況作為分組結果,即將所有EP分為GE1 = (P1,P3,P4,P5,P7)、
,此時Nout=50,ρ4 = 0.372.由於ρ2最小,因此選擇它所對應的分組情況作為分組結果,即將所有EP分為GE1 = (P1,P3,P4,P5,P7)、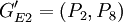 和
和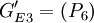 3個組.由此得到CR與工程性能組的關係矩陣
3個組.由此得到CR與工程性能組的關係矩陣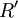 ,如表所示
,如表所示
某數控機床用戶需求與工程性能組的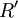 矩陣
矩陣
| 用戶需求 | 工程性能組 | ||
|---|---|---|---|
| GE1 | 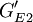 | 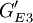
| |
| Q1 | 21 | 3 | 3 |
| Q2 | 0 | 18 | 3 |
| Q3 | 7 | 1 | 0 |
| Q4 | 7 | 1 | 0 |
| Q5 | 8 | 4 | 9 |
| Q6 | 21 | 3 | 0 |
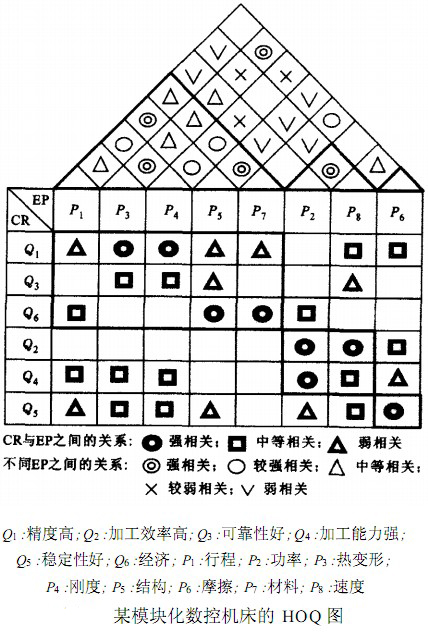
採用遺傳演算法,求解式(3)~式(5),得到G1 = (Q1,Q3,Q6,GE1) = (Q1,Q3,Q6,P1,P3,P4,P5,P7),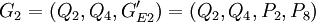 ,
,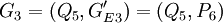 ,此時maxV(x)=88
,此時maxV(x)=88
分塊後的HOQ矩陣如下圖所示,其中第1組(G1)包括了行程、熱變形、剛度、結構、材料等工程性能,它們都涉及到機床的結構特性.由於機床的結構在很大程度上取決於其材料和行程,因此它們之間具有較大的耦合繫數,而機床剛度和行程、材料以及熱變形也是相互緊密聯繫的,因此將行程、熱變形、剛度、結構、材料等歸為一組是合理的.與之相關的用戶需求是機床的精度、可靠性和經濟性,這些用戶需求都需要通過機床結構、材料、行程、剛度、熱變形等工程性能加以實現,因此它們之間具有緊密的聯繫,在設計中可以作為一個模塊來考慮。第2組(G2)包括了功率和速度,它們反映了機床的運動學特性,與機床的速度和功率緊密相關,主要用於滿足用戶對機床的加工效率與加工能力的需求,因此將其歸為一組也是合理的。第3組(G3)只包括摩擦雖然它與機床材料以及熱變形都有關係,但與第1組的其他工程性能之間聯繫並不大,故將摩擦特性單獨列出。摩擦在很大程度上影響著機床的穩定性因此將摩擦和機床的穩定性作為一個模塊。由於模塊劃分結果與實際狀況相符,因此證明瞭本文基於HOQ矩陣的兩階段產品模塊化分組方法的有效性。
互相關矩陣為基礎,通過將其轉化為工程性能的相似度矩陣,藉助max-min分組方法,將複雜的分組問題轉化為可由電腦處理的Fiedler特征值及其特征向量的求解問題,並以平均損失度作為分組優劣的依據,實現對工程性能的分組.在得到分組數的條件下,再以用戶需求與工程性能的關係矩陣為基礎,通過求解簡單的0-1整型規劃問題實現對用戶需求的分組.通過對某機床設計的運行實例表明,採用本文的方法可得到較為合理的產品設計模塊劃分,從而為從HOQ矩陣出發實現機械產品模塊化的概念設計,以及將複雜的設計問題進行簡化提供了工具。
評論(共21條)
案例看不明白
增加了一個新的案例,希望對你有幫助!
這個名詞是誰提出的?什麼年代提出的?
美國學者Hauser和Clausing於1988年提出的
我認為正是大規模的產品才適用這種方法,小產品可以通過復用解決。功能多時利用質量屋可以很好的跟蹤管理,而至於方法本身,完全可通過電腦輔助解決。
有改進方式嗎?畢竟不適合大型系統的應用
可以結合數量化理論3類,模糊層次分析法,信息熵等方法進行優化。個人認為非常適合大型系統,反倒不適合小型系統。
美國學者Hauser和Clausing於1988年提出的
詳見1988年哈佛商業評論上的著名論文《The House of Quality》,具有劃時代的意義。
這個名詞是誰提出的?什麼年代提出的?
本文第一句話就說明瞭喲!









寫得很好