市場整合

出自 MBA智库百科(https://wiki.mbalib.com/)

　　市場整合是指在市場完全競爭的情況下，同類商品在不同市場上的價格保持同步變化，是經濟資源.合理流動的反映，體現市場運行的效率。

　　市場整合理論是在實踐中不斷地發展和完善的，主要包括不同空間市場的整合、不同營銷階段的整合、不同時間和不同商品的整合。

　　在研究過程中，又有學者提出垂直整合的概念，從而使市場整合的範圍越來越廣泛。

　　空間市場整合(Spatial Market Integration)。是研究某一市場價格變化對另一市場價格變化影響的程度。從理論上講，在完全競爭的假設下，處於不同區域的市場之間進行貿易時，某產品在輸入區的單價等於該產品在輸出區的價格加上單位運輸成本，因而，輸出區的價格變化會引起輸入區價格的同樣方向和同等程度的變化，如此則稱為此兩個市場是完全整合的。空間市場整合通常可分為長期市場整合和短期市場整合兩種。長期整合指兩個市場的價格之間存在長期的、穩定的聯繫，即使這種長期均衡關係在短期內被打破、但最終也會恢復到原來的均衡狀態。短期整合指某一市場該產品價格的變化，會立即在下一期引起另一市場上該產品價格的變化，他反映了市場之間產品價格傳遞的及時性和價格反映的敏感性。如果某個國家的任何兩個市場之間都是整合的，則稱這個國家的市場是整合的或一體化的。實際上，任何一個國家的市場都不可能完全整合，完全整合是一種理論上的狀態。

　　營銷階段的整合(Integratinaeross Price Form)。不同營銷階段的整合，主要研究同一商品在某營銷階段的價格變化對下一階段價格變化的影響程度。如果某商品在不同營銷階段的價格滿足“下一階段價格二上一階段價格+營銷成本”，則此營銷階段之間是整合的。如批零市場整合，即某商品的批發市場和零售市場之間的整合。

　　市場的時間整合(Temperal Market Integration)。時間整合主要研究某商品的現期價格變化對後期價格變化的影響程度。當滿足“後期價格二現期價格+儲藏費用”時，則稱為時間整合。

　　相關商品間的整合(Integratinaeross Produet Form)。相關商品間的市場整合，主要研究某商品的價格變化對其相關商品價格變化的影響程度，多數是考察初級產品和加工品之間或原料和產品之間的價格影響關係，如果滿足“加工品價格=初級產品價格+加工費用”，則這些商品之間的市場是整合的。對相關產品之間市場整合的研究，具有很重要的意義，它可以科學地反映兩種產品之間的比價是否合理，反映兩種商品價格之間的相互影響和商品市場之間的相互協調關係，能夠從本質上揭示市場運行的效率。

　　根據市場整合的概念，可以推論，任何影響產品在市場間的流通，或影響產品在不同市場上的價格水平的因素均會影響市場整合水平。影響市場整合的主要因素如下:

　　1.價格信息。包括價格信息是否可以得到，價格信息的質量及獲取價格信息的速度。如果缺乏市場價格信息，市場間的套利行為(arbitrage)或者不可能發生或者會帶有很大的盲目性。不准確的價格信息會影響市場間套利行為的結果。信息流通的速度則會影響市場間套利行為發生的快慢進而影響市場整合的速度。

　　2.運輸條件。包括市場間有無道路航線，道路狀況及運輸方法和設施。道路條件好能減少產品運輸所需時間。先進的運輸方法與設施既能縮短運輸時間也能提高運輸效率。與運輸有關的另一個因素是運輸距離。原則上講，運輸距離不會成為市場整合的障礙，儘管運輸距離會在一定程度上影響市場整合速度。不過，市場間距離長短會影響市場整合研究的資料選用。

　　3.政府干預。政府干預多會減弱市場整合程度，甚至會完全割斷市場間的價格關係。在這種情況下，無論高質量的價格信息如何可以快速獲取，也無論運輸條件有多好，市場間的套利行為均不大可能發生。

　　其他影響市場整合程度的因素包括私有商業經濟的發展程度及其規模大小和可用於市場間進行套利活動的產品數量的大小。私商的套利行為是推動市場整合的一個重要力量。私營商業的正常發展，有助於大型私營企業的產生。相對於規模較小的私營企業，大企業融資容易，資金較足，經營設施先進，所有這些均會促進市場整合。另外，可用於市場間套利活動的產品數量大也有利於市場整合。如果產品的絕大部分由政府壟斷經營，可被私商用於套利的數量微乎其微，那麼，除非政府部門的經營效率高，市場整合的程度一般來說難以改善。

　　市場整合測定主要是通過考察市場價格變動關係來進行的。自Lele(1967)的文章發表以來，研究人員推出了不少新的分析方法。除極少被採用的方差分析法(Variance analysis)之外，用以檢驗市場整合的方法大致有四種:相關分析法(The correlation analysis method) );Ravallion模型法(The Ravallion procedure);共聚合法(The cointegration approach)及Paritybounds模型法(The parity bounds model)。

　　相關分析法。作為檢測區間市場整合的一種方法，相關分析法流行了較長時間。主要是因其簡單易用。對於同種產品，計算其不同市場兩個價格序列間的相關係數。如果該繫數在統計上顯著，通常則認為這兩個市場是具有整合關係的。使用這種方法的有Lele(1967)，Tnakur(1974)及Ejiga(1977)。

　　這種靜態的分析方法存在不少問題。較高的相關係數可能是由其他因素引起的，如類似的供需格局;由通脹、季節性等因素引起的共同趨勢在計算中未予處理;政府的價格干預，等等。因此，在同市場的價格序列間可能存在較高的相關程度，但這些市場間並不存在整合關係。同樣地，儘管較低的相關係數通常意味著市場間可能不存在或僅存在微弱的整合關係，但這些市場也有可能是整合的。導致這種現象的原因有:某市場既是重要的供給中心，同時也是重要的消費中心(Blyn 1973);使用非同種同質產品的價格資料(Harriss 1979);不同時期的成本變動(如運輸費用變動)(Wyeth 1992)。

　　Ravallion模型法。Ravallion對靜態的二元相關分析方法作了延伸和改進，推出了頗為有名的Ravallion模型法(Ravallion 1986)。該方法假設有一個輻射型市場格局存在。處於中央的市場為參照市場(reference market)或叫中心市場(central market)。周邊市場的價格受中心市場的價格所支配或影響，這種關係可表達為:

　　(1)P_i = f_i(R,X_i)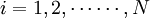

　　這裡`P'代表第i個周邊市場的價格，`R'則為中心市場的價格，`X'是一向量，包括影響第i個市場價格的其他因素。同時，中心市場的價格也是所有周邊市場價格的函數，即:

　　(2)

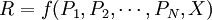
　　如果考慮滯後價格的影響，那麼上述兩種模型即被賦予了一種動態結構，即:

　　(3)P_it = a_iP_{it − 1} + b_i0R_t + b_i1R_{t − 1} + c_iX_it + ε_it ,　　　　　　

　　(4)

　　上述模型中，僅有方程(3)用於通常的估算，且方程(3)還可改寫成如下形式:

　　(5)(P_t − P_{t − 1}) = d₀ + d₁(P_{t − 1} − R_{t − 1}) + d₂(R_t − R_{t − 1}) + d₃R_{t − 1} + d₄X + ε_t

　　該形式具有“誤差校正機制”(error correction mechanism)，可用普通最小二乘法進行估算。Ravallion模型剋服了許多相關分析法在統計推斷方面的問題，併在模型中引入了動態因素。該模型可檢測短期和長期市場整合關係。使用Ravallion模型的有Timmer(1987)，Wu(1994)，Cheng和Wu(1995)。

　　儘管Ravallion方法與相關分析法相比有了不少改進，但它仍存在局限性。第一，相對於周邊市場而言，中心市場也許並不是外生的。也就是說儘管周邊市場的價格變動取決於中心市場的價格變動，但反過來可能也成立。這就意味著方程(5)中，中心市場項(R)和誤差項(ε)系非相互獨立。在這種情況下，普通最小二乘法估計則是有偏的(biased)和不一致的(inconsistent)。第二，很多時間序列數據都有趨勢(trend)問題。除非單個價格序列是“聚合”的(in-tegrated)，且兩兩“共聚合”(cointegrated)，否則，用普通最小二乘法估算Ravallion模型是不可能的或不合適的(Weyth 1992)。第三，Ravallion模型需要假設一個幅射型市場的存在並有一個固定的中心市場。現實不一定如此，更有可能的是多個市場相互影響。另外，某一時期的中心市場，在另一時期，有可能被其它市場所取代。

　　共聚合法。該方法在很大程度上系Ravallion方法的延伸和改進。它保留了Ravallion方法的長處而剋服了其短處。最初將共聚合技術用於區間市場分析見於Goodwin和Schroeder(1991)。之後，共聚合法受到研究人員極大關註並不斷予以改善。見Wyeth(1992)，Palaskas和Harriss-White(1993)，Alexander和Wyeth(1994)及Dercon(1995)。在檢驗不同市場間價格序列的共聚合(cointegration)之前，通常需要檢驗單個價格序列是否自身為同階聚合(integrated to the same order)的。因而使用共聚合方法的第一步是，確立每一價格序列的聚合階數(order of integration)。如果有相關的價格具有相同的聚合階數這是較普遍的現象，那麼就可以應用共聚合法。

　　以i和j分別代表位於不同區域的兩個市場，P為某產品的價格。那麼所需要的共聚合模型可表示為:　　　(6)P_it = δ + αP_jt + v_t

　　如果P_i和P_j各自於同階聚合且V_t於零階聚合，那麼P_i和P_j是共聚合的。這便意味著市場與市場之間存在長期的整合關係。為了確定市場信息在市場間流動的方向，可作如下因果關係檢驗(Granger-causality test)。先估算下列方程式:

　　(7)

　　(8)

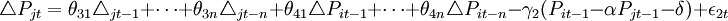
　　然後再檢驗下列假設:

　　(9)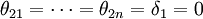 　　　　(從P_j到P_i沒有因果關係)

　　(10)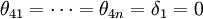 　　　　(從P_i到P_j沒有因果關係)

　　最後一步是估算方程(7)的結構式。其結構方程式為:

　　(11)

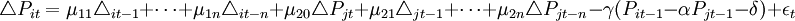
　　估算該方程式有兩個目的。一是檢驗有無短期市場整合存在;二是進一步核實方程(6)的長期市場整合的檢驗。短期市場整合意味著某一市場的價格變化會“立即”引起另一市場價格的變化，也就是:　　　(12)

　　另外，如果長期市場整合確實存在，那麼下述假設應該成立:

　　共聚合技術用於市場整合研究以來，頗受研究人員的青睞。除前面提到的用共聚合法研究市場整合的例子外，Zhou，Wanand Chen(1997a，1997b)和喻、黃(1998)均使用該法研究中國稻米市場的整合問題。

　　共聚合法也有其不足之處。該檢驗方法僅能提供“或者全有，或者全無”的結論。在現實生活中，市場間的關係一般不會是那麼簡單。有時即使使用經濟計量方法未測出整合關係，市場間有可能已處於逐步的整合過程中。另外，儘管Dercon(1995)曾考慮結構變化(如突然引進或取消市場干預，戰爭的爆發或結束等)對市場整合的影響，但其方法不夠規範化。在結構變化的情況下市場整合的技術尚待完善。

　　Parity Bounds模型法。所有上述三種市場整合研究方法均只考慮不同市場的價格變動情況。Baulch(1997)認為在研究市場整合時，僅考慮價格變動而不考慮運輸成本是不夠的。他建議使用Parity Bounds模型方法。該模型試圖同時使用價格和平均運輸成本資料來考察市場運作效率。它允許運輸成本在不同時期變動，也可以使用不完整的時間序列資料。有關該方法的細節請見Baulch(1997)。

　　Parity Bounds模型法也有缺陷。第一，該模型估計僅使用現期價差資料(contemporaneous spreads)，故很難將滯後的價格調整因素納入模型估計中去(Ravallion模型及共聚合模型均可做到這一點)。第二，模型估算需要準確的運輸成本資料或運輸成本估算值，如果成本資料估計值欠準確，那麼整個市場整合分析結果將令人生疑。可在現實生活中，有些非正常運輸成本資料，如以取得運輸能力為目的的賄賂開支是幾乎不可能獲取或估算的。