因果關係檢驗
出自 MBA智库百科(https://wiki.mbalib.com/)
因果關係檢驗 (Causality test)
目錄 |
經濟學家開拓了一種可以用來分析變數之間的因果的辦法,即格蘭傑因果關係檢驗。該檢驗方法為2003年諾貝爾經濟學獎得主克萊夫·格蘭傑(Clive W. J. Granger)所開創,用於分析經濟變數之間的因果關係。他給因果關係的定義為“依賴於使用過去某些時點上所有信息的最佳最小二乘預測的方差。”
在時間序列情形下,兩個經濟變數X、Y之間的格蘭傑因果關係定義為:若在包含了變數X、Y的過去信息的條件下,對變數Y的預測效果要優於只單獨由Y的過去信息對Y進行的預測效果,即變數X有助於解釋變數Y的將來變化,則認為變數X是引致變數Y的格蘭傑原因。
進行格蘭傑因果關係檢驗的一個前提條件是時間序列必須具有平穩性,否則可能會出現虛假回歸問題。因此在進行格蘭傑因果關係檢驗之前首先應對各指標時間序列的平穩性進行單位根檢驗(unit root test)。常用增廣的迪基—富勒檢驗(ADF檢驗)來分別對各指標序列的平穩性進行單位根檢驗。
(1)將當前的y對所有的滯後項y以及別的什麼變數(如果有的話)做回歸,即y對y的滯後項yt-1,yt-2,…,yt-q及其他變數的回歸,但在這一回歸中沒有把滯後項x包括進來,這是一個受約束的回歸。然後從此回歸得到受約束的殘差平方和RSSR。
(2)做一個含有滯後項x的回歸,即在前面的回歸式中加進滯後項x,這是一個無約束的回歸,由此回歸得到無約束的殘差平方和RSSUR。
(3)零假設是H0:α1=α2=…=αq=0,即滯後項x不屬於此回歸。
它遵循自由度為q和(n-k)的F分佈。在這裡,n是樣本容量,q等於滯後項x的個數,即有約束回歸方程中待估參數的個數,k是無約束回歸中待估參數的個數。
(5)如果在選定的顯著性水平α上計算的F值超過臨界Fα值,則拒絕零假設,這樣滯後x項就屬於此回歸,表明x是y的原因。
(6)同樣,為了檢驗y是否是x的原因,可將變數y與x相互替換,重覆步驟(1)~(5)。
因果關係檢驗的案例
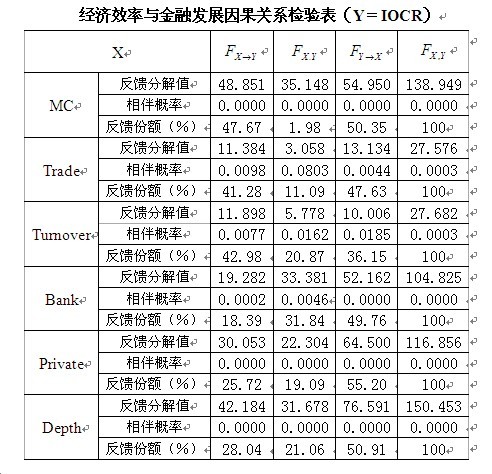
根據Geweke分解檢驗的原理,利用經濟計量學軟體Eviews5.0 ,我們對金融發展與經濟效率的因果關係進行實證研究,研究結果詳見下圖
根據上圖的實證結果,我們可以發現我國金融發展與經濟效率有如下關係:
(1)、從反饋分解值及其相伴概率來看,我國的金融發展與經濟效率呈現顯著的雙向因果關係。對於金融發展,無論是金融深化程度,還是銀行和股票市場的發展都與經濟效率有顯著的雙向因果關係。
(2)、從反饋份額來看,金融發展與經濟效率的反饋關係更多表現為經濟效率對金融發展的因果關係。
(3)、從即時因果關係看,金融發展與經濟效率的即時因果關係都顯著。由此可見,金融發展不僅從長期看與經濟效率相互影響,而且在其短期變動上與經濟效率也顯著相互影響。
雖然變數的不平穩性是造成虛假因果關係最主要的因素之一,但是小樣本的存在則會犯真實因果關係檢驗不出的錯誤。隨著樣本容量的逐漸增大,判斷出兩個平穩序列存在Granger因果關係的概率將顯著增大。尤其是當樣本數量小於20的情況下,如果經Granger因果關係檢驗結果為“存在因果關係”,則可以用90 以上的概率保證所研究變數間存在真實的因果關係,反之,如果檢驗結果為“不存在因果關係”,則不能斷定變數間不存在真實的因果關係。