隱性變數法
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
隱性變數法(latent variable approach ,LV)
目錄 |
[編輯]
隱性變數法的基本思路是,將全要素生產率視為一個隱性變數即未觀測變數,從而藉助狀態空間模型(state space model) 利用極大似然估計給出全要素生產率估算。
[編輯]
具體估算中,為了避免出現偽回歸,需要進行模型設定檢驗包括數據平穩性檢驗和協整檢驗。平穩性檢驗和協整檢驗的方法很多,常見的有ADF (the Augmented Dickey-Fuller) 單位根檢驗和JJ(Johanson and Juselius ,1990) 協整檢驗。由於產出、勞動力和資本存量數據的趨勢成分通常是單位根過程且三者之間不存在協整關係,所以往往利用產出、勞動力和資本存量的一階差分序列來建立回歸方程。採用C - D 生產函數,且假設規模收益不變,則有如下觀測方程:
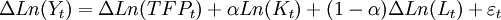(1)
其中,ΔLn(TFPt) 為全要素生產率增長率,假設其為一個隱性變數,且遵循一階自回歸即AR 過程,則有如下狀態方程:
ΔLn(TFPt) = ρΔLn(TFPt − 1) + υt (2)
其中,ρ為自回歸繫數,滿足| ρ| < 1 ,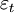
為白雜訊。這樣,利用狀態空間模型,通過極大似然估計同時估算出觀測方程(1) 和狀態方程(2) ,從而得到全要素生產率增長的估算值。隱性變數法的最大優點在於,不再將全要素生產率視為殘差,而是將其視為一個獨立的狀態變數,這樣將全要素生產率從殘差中分離出來,從而剔除掉一些測算誤差對全要素生產率估算的影響。同時,在具體估算時,還充分考慮了數據非平穩性帶來的偽回歸問題。
[編輯]
隱性變數是在模型設定中使用的一種變數，該變數不能實際觀察到，但又是確實存在的，如經濟信心指數，生活幸福指數等。使用該變數後可以簡化模型，減少待估計的參數個數。