休哈特控製圖
出自 MBA智库百科(https://wiki.mbalib.com/)
控製圖(Control Chart)
目錄 |
休哈特控製圖是由美國的貝爾電話實驗所的休哈特(W.A.Shewhart)博士在1924年首先提出管製圖使用後,管製圖就一直成為科學管理的一個重要工具,特別在質量管理方面成了一個不可或缺的管理工具。它是一種有控制界限的圖,用來區分引起質量波動的原因是偶然的還是系統的,可以提供系統原因存在的信息,從而判斷生產過程是否處於受控狀態。控製圖按其用途可分為兩類,一類是供分析用的控製圖,用控製圖分析生產過程中有關質量特性值的變化情況,看工序是否處於穩定受控狀;再一類是供管理用的控製圖,主要用於發現生產過程是否出現了異常情況,以預防產生不合格品。
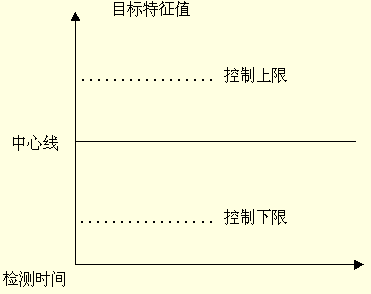
控製圖畫在平面直角坐標系中,橫坐標表示檢測時間,縱坐標表示測得的目標特征值。按控制對象(目標特征值)的變化情況,控製圖又分為兩種:一種是穩值控製圖,一種是變值控製圖。
1、穩值控製圖。穩值控製圖一般用於對產品質量或目標值恆定不變的目標實施狀態進行控制,如下圖所示,圖中中心線表示計劃目標值,虛線表示控制上下限。
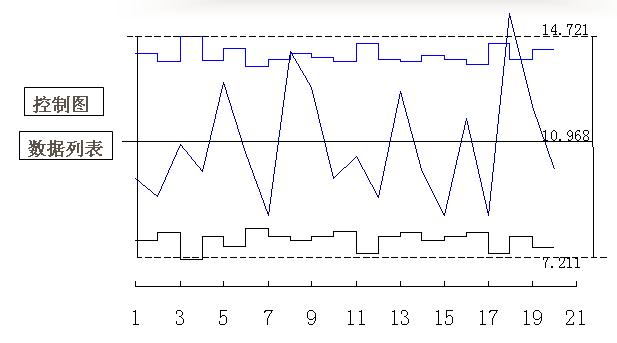
2、變值控製圖。變值控製圖用於對目標值隨時間變化的目標實施狀態進行控制。從計劃線與實際線的對比,可看出目標實施狀態,對於超出計劃線的情況,查清超出的原因,採取措施,將其控制在計劃線以下。
控製圖是對過程質量加以測定、記錄從而進行控制的一種科學方法。圖上有中心線、上只存在偶然波動時,產品質量將形成某種典型分佈。例如,在車制螺絲的例子中形成正態分佈。如果除去偶然波動外還有異常波動,則產品質量的分佈必將偏離原來的典型分佈。因此,根據典型分佈是否偏離就能判斷異常因素是否發生,而典型分佈的偏離可由控製圖檢出。在上述車制螺絲的例子中,由於發生了車刀磨損的異常因素,螺絲直徑的分佈偏離了原來的正態分佈而向上移動,於是點子超出上控制界的概率大為增加,從而點子頻頻出界,表明在異常波動。控製圖上的控制界限就是區分偶然波動與異常波動的科學界限,休哈特控製圖的實質是區分偶然因素與異常因素兩類因素。
1.控製圖的預防原理
控製圖是如何貫徹預防原則的呢?這可以由以下兩點看出:
(1)應用控製圖對生產過程不斷監控,當異常因素剛一露出苗頭,甚至在未造成不合格品之前就能及時被髮現,在這種趨勢造成不合格品之前就採取措施加以消除,起到預防的作用。
(2)在現場,更多的情況是控製圖顯示異常,表明異常原因已經發生,這時一定要貫徹“查出異因,採取措施,保證消除,不再出現,納人標準。” 否則,控製圖就形同虛設,不如不搞。每貫徹一次(即經過一次這樣的迴圈)就消除一個異常因素,使它不再出現,從而起到預防的作用。
2.統計過程式控制制的實質
要精確地獲得總體的具體數值,需要收集總體的每一個樣品的數值。這對於一個無限總體或一個數量很大的有限總體來說往往是不可能的,或者是不必要的。在實際工作中,一般是從總體中隨機地抽取樣本,對總體參數進行統計推斷。樣本中含有總體的各種信息,因此樣本是很寶貴的。但是如果不對樣本進一步提煉、加工、整理,則總體的各種信息仍分散在樣本的每個樣品中。為了充分利用樣本所含的各種信息,常常把樣本加工成它的函數,一般將這個(或若幹個)不含未知參數的樣本函數稱為統計量。
過程式控制制的實質,就是這樣一個統計推斷過程,所依據的統計量的形式應根據計推斷的目的和應用的條件不同而有所不同。從實用和簡化計算的角度來看,往往是利用樣本的平均值和極差R來進行。
值得註意的是,利用樣本的平均值 及極差R推斷總體的μ和σ時,由於總體構成的不均勻性以及抽樣誤差的存在,
及極差R推斷總體的μ和σ時,由於總體構成的不均勻性以及抽樣誤差的存在, 及R的變化同μ及σ的變化並不完全一樣,即使在工序處於穩定狀態下,μ及σ本身並無異常變化,但從工序中抽取樣本的
及R的變化同μ及σ的變化並不完全一樣,即使在工序處於穩定狀態下,μ及σ本身並無異常變化,但從工序中抽取樣本的 及R也是有所變化的也就是說,
及R也是有所變化的也就是說, 及R 都是隨機變數,都有其特定的概率分佈。它們各自的概率分佈與總體分佈既有一定的內在聯繫,又與總體分佈不完全相同。在過程式控制制中,雖然通常依據一次抽樣的結果進行一次統計推斷,但由此所得出的結論卻是建立在大量觀測結果所遵循的統計規律的基礎上的,是依樣本統計量的概率分佈來描述總體概率分佈過程的。
及R 都是隨機變數,都有其特定的概率分佈。它們各自的概率分佈與總體分佈既有一定的內在聯繫,又與總體分佈不完全相同。在過程式控制制中,雖然通常依據一次抽樣的結果進行一次統計推斷,但由此所得出的結論卻是建立在大量觀測結果所遵循的統計規律的基礎上的,是依樣本統計量的概率分佈來描述總體概率分佈過程的。
1.計量值控製圖
常用的計量值控製圖有:平均值與極差控製圖(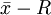 圖)中位數與極差控製圖(
圖)中位數與極差控製圖(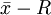 圖)等等。其中尤以
圖)等等。其中尤以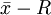 圖用得最多,它對加工工序有很強的控制能力,是控制產品質量最實用有效的一種工具
圖用得最多,它對加工工序有很強的控制能力,是控制產品質量最實用有效的一種工具
2.計數值控製圖
常用計數值控製圖由:不合格品數控值圖;不合格品率控製圖和單位缺陷控製圖,缺陷控製圖。
3.應用控製圖需要考慮的問題
應用控製圖需要考慮以下一些問題:
(1)控製圖用於何處?原則上講,對於任何過程,凡需要對質量進行控制管理的場合都可以應用控製圖。但這裡還要求:對於所確定的控制對象—— 質量指標應能夠定量,這樣才能應用計量值控製圖。如果只有定性的描述而不能夠定量,那就只能應用計數值控製圖。所控制的過程必須具有重覆性,即具有統計規律。對於只有一次性或少數幾次的過程顯然難於應用控製圖進行控制。
(2)如何選擇控制對象?在使用控製圖時應選擇能代表過程的主要質量指標作為控制對象。一個過程往往具有各種各樣的特性,需要選擇能夠真正代表過程情況的指標。例如,假定某產品在強度方面有問題,就應該選擇強度作為控制對象。在電動機裝配車間,如果對於電動機軸的尺寸要求很高,這就需要把機軸直徑作為我們的控制對象。
(3)怎樣選擇控製圖?選擇控製圖主要考慮下列幾點:首先根據所控制質量指標的數據性質來進行選擇;其次,要確定過程中的異常因素是全部加以控制(全控)還是部分加以控制(選控),若為全控應採用休哈特圖等;若為選控,應採用選控圖。
(4)如何分析控製圖?如果控製圖中點子未出界,同時點子的排列也是隨機的,則認為生產過程處於穩態或控制狀態。如果控製圖中點子出界(或不出界)而點子的排列是非隨機的(也稱為排列有缺陷),則認為生產過程失控。
(5)對於點子出界或違反其他準則的處理。若點子出界或點子的排列是非隨機的,則應立即追查原因並採取措施防止它再出現。
(6)對於過程而言,控製圖起著報警鈴的作用,控製圖點子出界就好比報警鈴響,告訴現在是應該進行查找原因、採取措施、防止再犯的時刻了。一般來說,控製圖只起報警鈴的作用,而不能告訴這種報警究竟是由什麼異常因素造成的。要找出造成異常的原因,除去根據生產和管理方面的技術與經驗來解決外,應該強調指出,應用兩種質量診斷理論和兩種質量多元診斷理論來診斷的方法是十分重要的。
(7)控製圖的重新制定。控製圖是根據穩定狀態下的條件5MIE來制定的。如果上述條件變化,如操作人員更換或通過學習操作水平顯著提高,設備更新,採用新型原材料或其他原材料,改變工藝參數或採用新工藝,環境改變等,這時,控製圖也必須重新加以制定。由於控製圖是科學管理生產過程的重要依據,所以經過相當時間的使用後應重新抽取數據,進行計算,加以檢驗。
- 一、計量值控製圖
(一).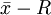 控製圖
控製圖
對於計量數據而言,這是常用最基本的控製圖。它的控制對象為長度、重量、純度、時間和生產量等計量值的場合。但此圖只適用於n<10的情況。
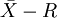 控製圖的分析
控製圖的分析
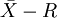 控製圖(以及
控製圖(以及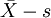 控製圖)是計量值最常用、最重要的控製圖。
控製圖)是計量值最常用、最重要的控製圖。
1. 適用範圍廣
 圖:若X服從正態分佈,則易證
圖:若X服從正態分佈,則易證 也服從正態分佈;若X非正態分佈,則根據中心極限定理,可證
也服從正態分佈;若X非正態分佈,則根據中心極限定理,可證 近似服從正態分佈。關鍵是這後一點才使
近似服從正態分佈。關鍵是這後一點才使 圖得以廣為應用。
圖得以廣為應用。
R圖:通過在電腦上的模擬試驗證實:只要X不是非常不對稱的,則R的分佈無大的變化,故也適用範圍廣。
2. 靈敏度高
 圖:對於偶波,
圖:對於偶波, 會使標準偏差減少,從而使控制線UCL和LCL的間隔縮小。對於異波,由於一般異波所產生的變異往往是同一個方向的,故求平均值的操作對其無影響,因此,當異常時,描點出界就更加容易了,也即靈敏度高。
會使標準偏差減少,從而使控制線UCL和LCL的間隔縮小。對於異波,由於一般異波所產生的變異往往是同一個方向的,故求平均值的操作對其無影響,因此,當異常時,描點出界就更加容易了,也即靈敏度高。
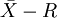 控製圖中,應該先作哪一個?
控製圖中,應該先作哪一個?
 圖與R圖控制線的公式:
圖與R圖控制線的公式:
 圖:
圖:
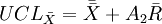
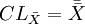
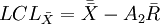
R圖:
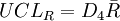
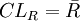
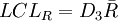
(1)若先  作圖,則由於R 圖還未判穩,
作圖,則由於R 圖還未判穩,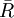 的數據不可用,故不可行。
的數據不可用,故不可行。
(2)若先作R圖,則由於R圖中只有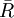 一個數據,所以可行。等R圖判穩後,再作
一個數據,所以可行。等R圖判穩後,再作 圖。
圖。
(3)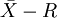 控製圖的操作步驟如下:
控製圖的操作步驟如下:
步驟1:確定所控制的質量指標
①選擇技術上最重要的控制對象
②指標之間有因果關係,取作為因的指標為統計量
③控制對象要明確,併為大家理解與同意
④控制對象要能以數字來表示
⑤控制對象要容易測定並對過程容易採取措施
⑥直接選擇控制對象困難時採用代用特性進行測定
⑦同時控制多個對象,應用多元控製圖與多元診斷
步驟2:取預備數據
① 樣本組數至少取25組,最好再加上5組成為30組,以便必要時可去掉一些異常數據;
② 樣本量(或樣本大小)通常取為4或5;
③ 合理子組原則。
步驟3:計算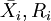 。
。
步驟4:計算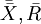
步驟5:計算R圖控制線、 圖控制線,並作圖。
圖控制線,並作圖。
步驟6:將預備數據在R圖中打點,判穩。若穩,則進行步驟7;若不穩,則執行“20字方針”後轉入步驟2,重新開始。
步驟7:將預備數據在 圖中打點,判穩。若穩,則進行步驟8;若不穩,則執行“20字方針”後轉入步驟2,重新開始。
圖中打點,判穩。若穩,則進行步驟8;若不穩,則執行“20字方針”後轉入步驟2,重新開始。
步驟8:計算過程能力指數並檢驗其是否滿足技術要求,若過程能力指數滿足技術要求,由轉入步驟9。
步驟9:延長X-R控製圖的控制線,作控制用控製圖,進行日常管理。
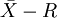 圖示例
圖示例
【例-1】某手錶廠為了提高手錶的質量,應用排列圖分析造成手錶不合格品的各種原因,發現“停擺”占第一位。為瞭解決停擺問題,再次應用排列圖分析造成停擺的原因,結果發現主要是由於螺栓脫落造成的。而後者則由螺栓鬆動造成。為此,廠方決定應用控製圖對裝配作業中的螺栓扭矩進行過程式控制制。
解:按照下列步驟建立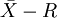 圖:
圖:
步驟1:取預備數據,將數據合理分成25組。
步驟2:計算各組樣本的平均數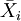 。
。
步驟3:計算各組樣本的極差Ri。
步驟4:計算樣本總均值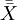 與平均樣本極差
與平均樣本極差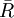 。
。
步驟5:計算R圖與 圖的參數,對狀態判斷。
圖的參數,對狀態判斷。
步驟6:與規範進行比較,計算過程能力。
步驟7:延長上述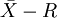 圖的控制線,對工序進行日常控制。
圖的控制線,對工序進行日常控制。
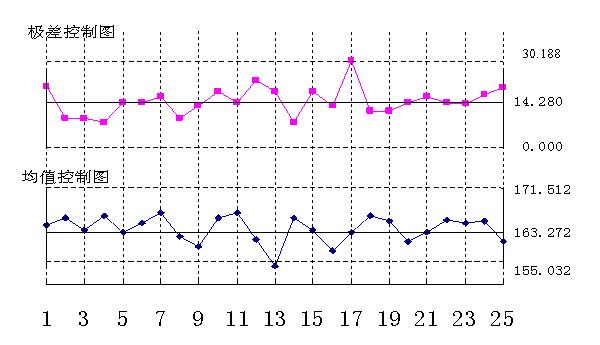
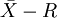 控製圖示例的第一次圖
控製圖示例的第一次圖
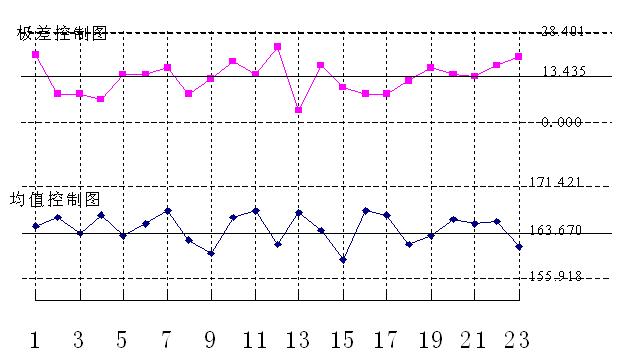
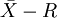 控製圖示例的第二次圖
控製圖示例的第二次圖
(二).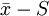 控製圖
控製圖
用標準差s控制總體參數σ的變化,當樣本大小n>10或12,這時應用極差估計總體標準差的效率降低,需要用S圖來代替R圖。
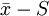 控製圖示例
控製圖示例
【例-2】對【例-1】選用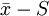 圖
圖
步驟1:依據合理分組原則,取得25組預備數據;
步驟2:計算每個子組的平均值和標準差;
步驟3:計算所有觀測值的總平均值和平均標準差;
步驟4:計算s圖的控制限,繪製控製圖;
步驟5:與容差限比較,計算過程能力指數;
步驟6:延長統計控制狀態下的控制限,進入控制用控製圖階段,實現對過程的日常控制。
(三).Me − R控製圖
用中位數圖代替均值圖。由於中位數的計算覺得,所以多用於現場需要把測定的數據直接記人控製圖進行控制的場合,這時為了簡便,當然規定奇數個數據。它受異常數據的影響較少。
Me-R圖示例
【例-3】某機器生產點子碟片。規定的厚度為0.007-0.016cm。每隔半小時抽取樣本量為5的樣本(子組),記錄其中心厚度(cm),如下表所示。擬建立一個中位數圖以達到控制質量的目的。
雲母碟片厚度的控制數據 單位:0.001
子組號i 厚度 中位數Me 極差Ri X1 X2 X3 X4 X5 1 14 8 12 12 8 12 6 2 11 10 13 8 10 10 5 3 11 12 16 14 9 12 7 4 16 12 17 15 13 15 5 5 15 12 14 10 7 12 8 6 13 8 15 15 8 13 7 7 14 12 13 10 16 13 6 8 11 10 8 16 10 10 8 9 14 10 12 9 7 10 7 10 12 10 12 14 10 12 4 11 10 12 8 10 12 10 4 12 10 10 8 8 10 10 2 13 8 12 10 8 10 10 4 14 13 8 11 14 12 12 6 15 7 8 14 13 11 11 7
(四).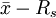 ,控製圖
,控製圖
為了能夠迅速反映現場情況,往往用X圖代替圖。
多用於下列場合:對每一個產品都進行檢驗,採用自動化檢查和測量的場合;取樣費時、昂貴的場合以及如化工等過程,樣品均勻,多抽樣也無太大的意義的場合。由於它不像前三種那樣能取得較多的信息,所以它判斷過程變化的靈敏都也要差一些。
X − Rs圖示例
【例-4】下表給出了連續10批脫脂奶粉的樣本“水分含量百分比”的實驗室分析結果。將一個樣本的奶粉作為一批的代表,在實驗室對其成分特性進行分析測試,如脂肪、水分、酸度、溶解指數、沉積物、細菌及乳清蛋白。希望該過程的產品水分含量控制在4%一下。由於發現單批內的抽樣變差可以忽略,因此決定每批只抽取一個觀測值,並以連續各批的移動極差作為設置控制限的基礎。
連續10個脫脂奶粉樣本的水分含量百分比
(X:%水分含量;R:移動極差)
批號 1 2 3 4 5 6 7 8 9 10 X 2.9 3.2 3.6 4.3 3.8 3.5 3.0 3.1 3.6 3.5 R 0.3 .04 0.7 0.5 0.3 0.5 0.1 0.5 0.1
二、計數值控製圖
1.p控製圖
用於控制對象為不合格品率或合格率等計數值質量指標的場合。常見的不良率有不合格品率、廢品率、交貨延遲率、缺勤率、差錯率等等。
當樣本量大小n變化時,則p圖的控制界限UCLp與LCLp將隨樣本大小n的變化呈現出凹凸狀,不便於判穩或判異。
圖-1 上下控制界線均呈現凹凸狀的p圖
2.np控製圖
用於控制對象為不合格品數的場合。由於計算不合格品率需要進行除法,比較麻煩,所以樣本大小相同的情況下,用此圖比較方便。但當樣本大小n變化時,np控製圖的三條控制線都呈凹凸狀,不但作圖難,而且無法判穩、判異。故只有在樣本大小相同的情況下,才應用此圖。
3.c控製圖
用於控制一部機器,一個部件一定的長度,一定的面積或任一定的單位中所出現的缺陷數目。但當樣本量n發生變化時,c圖上、中、下控制線將呈凹凸狀,不便於判穩或判異。
4.U控製圖
當樣品的大小保持不變時可用C控製圖,而當樣品的大小變化時則應換算為平均每單位的缺陷數後再使用U控製圖。但當n發生變化時,u圖的二條控制線將呈凹凸狀,給作圖、判異、判穩造成困難。
控製圖判斷異常的準則有兩條:點子出界就判斷異常;界內點排列不隨機判斷異常。
1.判斷穩態的準則
穩態是生產過程追求的目標。那麼如何用控製圖判斷過程是否處於穩態?為此,需要制定判斷穩態的準則。
判穩準則:在點子隨機排列的情況下,符合下列各點之一就認為過程處於穩態:
(1)連續25個點子都在控制界限內;
(2)連續35個點子至多1個點子落在控制界限外;
(3)連續100個點子至多2個點子落在控制界限外。
2.判斷異常的準則
在討論控製圖原理時,已經知道點子出界就判斷異常,這是判斷異常的最基本的一條準則。為了增加控製圖使用者的信心,即使對於在控制界限內的點子也要觀察其排列是否隨機。若界內點排列非隨機,則判斷異常。
判斷異常的準則:符合下列各點之一就認為過程存在異常因素:
(1)點子在控制界限外或恰在控制界限上控制界限內的點子排列;
(2)鏈:連續鏈,連續7個點以上排列在一側;間斷鏈,大多數點在一側
(3)多數點靠近控制界限(在2-3倍的標準差區域內出現)
(4)傾向性與周期性。
休哈特控製圖不適應性的分析[1]
- 1.不適應性的現象
現代製造模式具有複雜性、非線性、時變性、連續性、不確定性和不完全性等特點。它們使得休哈特控製圖難以適應的具體表現為:質量數據採集量不足;有些工序數據不是正態分佈;有些工序數據是大量的、海量的,如線上質量控制,由於電腦按時序線上採集數據,會致使工序質量數據量是大量的、海量的;質量控制要面對多過程和多參數;由於電腦集成製造和智能製造環境下的質量參數具有連續性、再現性等特點,致使質量數據相互相關;有的工序質量達到或接近零不合格過程,如時序參數長時間幾乎不發生變化或微小變化,致使休哈特控製圖在應用中失去判異作用,等等;形成了休哈特控製圖不適應性的新環境。
- 2.應用條件和原理上的局限性
休哈特控製圖是基於數理統計的原理,對生產過程中產生的系統原因進行識別並加以控制,從而達到對產品在生產過程中的質量控制,其應用條件主要有3個:
(1)質量特征數據是大批量的(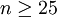 ,一般
,一般 );。
);。
(2)質量特征數據是呈正態分佈,或者接近正態分佈;
(3)質量特征變數相互獨立。即是判斷隨機變數X的數學問題;
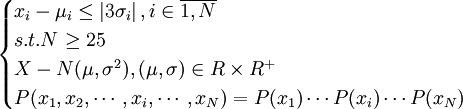
實際情況只要與3個應用條件之一發生衝突,就會發生休哈特控製圖應用條件的限制。而休哈特控製圖本身還存在精度不夠的問題,以及休哈特控製圖對數據量微小變化的遲鈍等,屬於休哈特控製圖原理上的局限性。
- 3.造成不適應性的原因和解決方案
造成休哈特控製圖的各種不適應性,其本質原因是應用條件的限制和原理上的局限性,前者導致了無法建立休哈特控製圖,後者僅僅運用休哈特控製圖已經達不到質量控制的目的;而客觀原因是採集數據與大批量製造模式相比發生了變化。解決不適應性問題的出路有兩個:一是化解本質原因,即改變休哈特控製圖的局限性,將原休哈特控製圖改造成為柔性動態的系統,由於以往休哈特控製圖的斐然成績,人們不習慣此改變;二是改變客觀原因,即調整或改造質量數據的變化,經過變換之後能夠適應休哈特控製圖的應用條件,這是可行的解決方法。同時,質量數據不僅是休哈特控製圖和其它質量控制方法的必要條件,還蘊涵著不同製造模式的特點。為此,需要分析各種製造模式與質量數據的關係,整理出規律,便於正確運用休哈特控製圖,達到質量控制的目的。
- ↑ 陳翔宇 梁工謙.休哈特控製圖在現代製造業中不適應性研究.《機床與液壓》.2006年12期
本条目由以下用户参与贡献
Vulture,苦行者,沙漠之鹰,山林,18°@鷺島,朱广文,Angle Roh,Kane0135,Cabbage,Error007,Dan,Dinging,Zfj3000,Yixi,连晓雾,方小莉.評論(共9條)
我認為控製圖的適用範圍必鬚生產過程要連續,像我們廠是搞軍品生產的,由於任務少,造成零配件加工量少,所以始終沒有開展過用控製圖控制生產過程工序加工質量。不知我這個說法有人認可嗎?歡迎討論。
我認為控製圖的適用範圍必鬚生產過程要連續,像我們廠是搞軍品生產的,由於任務少,造成零配件加工量少,所以始終沒有開展過用控製圖控制生產過程工序加工質量。不知我這個說法有人認可嗎?歡迎討論。
任務少,一樣可以用控製圖,橫軸可以調整為產量,這樣分佈就均勻了。
我認為控製圖的適用範圍必鬚生產過程要連續,像我們廠是搞軍品生產的,由於任務少,造成零配件加工量少,所以始終沒有開展過用控製圖控制生產過程工序加工質量。不知我這個說法有人認可嗎?歡迎討論。
數量少也有的用,三言兩語說不清,《戴明論質量管理》有專門談到這一點,不妨找來研度一下。
我認為控製圖的適用範圍必鬚生產過程要連續,像我們廠是搞軍品生產的,由於任務少,造成零配件加工量少,所以始終沒有開展過用控製圖控制生產過程工序加工質量。不知我這個說法有人認可嗎?歡迎討論。
那麼臭鼬工廠這種低速率的也不用麽?那麼如何保證好的學習曲線和產品質量呢?








請問怎樣可以看懂