不良率管製圖
出自 MBA智库百科(https://wiki.mbalib.com/)
不良率管製圖(Percent Defectives Control Chart)
目錄 |
不良率管製圖的統計理論基礎為二項分配,假設製程處於穩定狀態,製程中不符合規格的機率為必而且連續生產之各單位是獨立的,因此每一生產的單位可以看成是白努利隨機變數,其參數為p。假如隨機抽取n個樣本,D是樣本中之不合格品數,則D屬於二項分配,其參數為n及p亦即
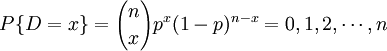
隨機變數D的平均數與變異數分別為np及np(1 − p)。樣本不良率之定義為:樣本中不合格品數目D與樣本大小n之比值
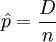
隨機變數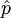 的分配從二項分配得知,因此
的分配從二項分配得知,因此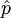 的平均數與變異數分別是
的平均數與變異數分別是
μ = p
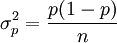
假設y為量測品質特性之樣本統計量,y之平均數為μy,標準差為σy,則蘇華特管製圖的一般型式為:
UCL = μy + kσy
中心線 = μy
LCL = μy − kσy
其中:UCL 表示控製圖的上控制界限; LCL 表示控製圖的下控制界限;
由於不良率管製圖主要管制製程不合格率必所以也稱為p管製圖,此管製圖雖然是用來管制產品之不合格率,但並非適用於所有之不合格率數據。在使用不良率管製圖時,要滿足下列條件:
1.發生一件不合格品之機率為固定。
2.前、後產品為獨立。如果一件產品為不合格品之機率,是根據前面產品是否為不合格品來決定,則不適合使用p管製圖。
3.如果不合格品有群聚現象時,也不適用p管製圖。此問題通常是發生在產品是以組或群之方式製造。例如在製造橡膠產品之化學製程中,如果烤箱之溫度設定不正確,則當時所生產之整批產品將具有相當高之不合格率。如果一產品被髮現為不合格,則同批之其他產品也將為不合格。
1.不良率p已知
假設不良率p已知,或p值由管理人員決定,則不良率管製圖的參數計算如下:
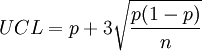
中心線=p
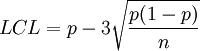
p管製圖之實施步驟包括抽取n個樣本,計算樣本不良率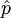 ,並將
,並將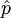 點在圖上,只要
點在圖上,只要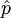 在管制界限內,且不存在系統性、非隨機性的變化,則可認為在水準p下,製程處於管制內(in control)。假設有任一點超出管制界限,或者存在非隨機性變化的情形,則表示製程的不良率已改變且製程不在管制內(out of control)。
在管制界限內,且不存在系統性、非隨機性的變化,則可認為在水準p下,製程處於管制內(in control)。假設有任一點超出管制界限,或者存在非隨機性變化的情形,則表示製程的不良率已改變且製程不在管制內(out of control)。
2.不良率p不知
若製程不良率p未知,則p值需從觀測數據中估計。一般的程式是初步選取m組樣本為n的樣本,通常m為20或25,假設第I組樣本含有Di個不合格品,則不良率為:
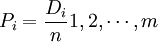
全體樣本之平均不良率為
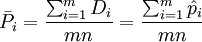
統計量為不良率p的估計值。 p管製圖中心線及管制界限之計算為:
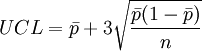
中心線=p
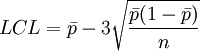
以上所得的管制界限稱為試用管制界限(trial control limits),它可先試用於最初的m組樣本,來決定製程正否在管制內。為了測試過去製程在管制內的假設,我們可先將m組樣本之不良率分別繪在管製圖上,然後分析這些點所顯示的結果。若所有的點均在試用管制界限內且不存有系統性的模型則表示過去製程正在管制內,試用管制界限能夠延用於目前或未來的製程。
假設有一點或更多點超出試用管制界限,則顯示過去的製程並非在管制內此時必須修正試用管制界限。其作法是檢查每一個超出管制界限的點找出其非機遇原因,然後將這些點捨棄,重新按相同之方法算出管制界限並檢查在圖上的點正否超出新的管制界限或存有非隨機性的模型。若有點超出。新的管制界限外,則須再修正管制界限,直到所有的點均在管制內。此時的管制界限才能延用於目前或未來的製程。
【例】某除草機製造商以p管製圖管制除草機在發動時是否正常。該公司每天抽取40部做試驗,第一個月之數據如下表所示,試建立試用管制界限。
| 日期 | 不合格品數 | 日期 | 不合格品數 | 日期 | 不合格品數 | 日期 | 不合格品數 |
|---|---|---|---|---|---|---|---|
| 1 | 4 | 7 | 1 | 13 | 7 | 19 | 0 |
| 2 | 3 | 8 | 3 | 14 | 2 | 20 | 1 |
| 3 | 1 | 9 | 0 | 15 | 3 | 21 | 3 |
| 4 | 2 | 10 | 1 | 16 | 3 | 22 | 2 |
| 5 | 3 | 11 | 2 | 17 | 2 | ||
| 6 | 2 | 12 | 4 | 18 | 8 |
【解】
由於每天抽樣之樣本數均相同,因此不合格率之平均值可以利用下式計算:
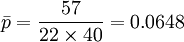
管制界限為
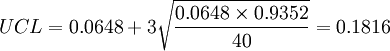
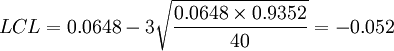
由於LCL < 0並無意義,因此我們將LCL設為0
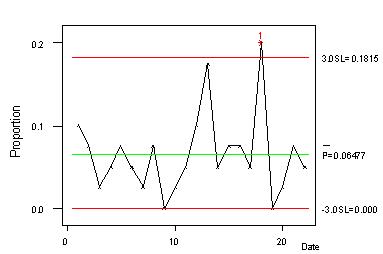
其p管製圖如下:
- 選擇品質特性
- 選擇樣本大小與樣本組數
- 收集數據
- 計算解析用中心線與解析用管制界限
- 繪製解析用不良率管製圖
- 建立管制用不良率管製圖
- 執行製程管制併進行持續性的品質改進








你這那是什麼管製圖啊。