亲爱的MBA智库百科用户：

过去的17年，百科频道一直以免费公益的形式为大家提供知识服务，这是我们团队的荣幸和骄傲。然而，在目前越来越严峻的经营挑战下，单纯依靠不断增加广告位来维持网站运营支出，必然会越来越影响您的使用体验，这也与我们的初衷背道而驰。因此，经过审慎地考虑，我们决定推出VIP会员收费制度，以便为您提供更好的服务和更优质的内容。

MBA智库百科VIP会员，您的权益将包括： 1、无广告阅读； 2、免验证复制。

当然，更重要的是长期以来您对百科频道的支持。诚邀您加入MBA智库百科VIP会员，共渡难关，共同见证彼此的成长和进步！

MBA智库百科项目组

2023年8月10日

百科VIP

无广告阅读

免验证复制

1年VIP

¥ 9.9

支付方式：

微信支付

支付宝

PayPal

购买数量：

1

应付金额：

9.9元

汇率换算：

1.32

美元(USD)

美元(USD)
加元(CAD)
日元(JPY)
英镑(GBP)
欧元(EUR)
澳元(AUD)
新台币(TWD)
港元(HKD)
新加坡(SGD)
菲律宾(PHP)
泰铢(THB)

按当月汇率换算，

包含手续费

打开手机微信扫一扫继续付款

立即开通

PayPal支付后，可能会遇到VIP权益未及时开通的情况，请您耐心等待，或者联系百科微信客服：mbalib888。

温馨提示：当无法进去支付页面时，可刷新后重试或更换浏览器
开通百科会员即视为同意《MBA智库·百科会员服务规则》

支付成功

全球专业中文经管百科，由121,994位网友共同编写而成，共计436,072个条目

查看

工具▼

缺點數管製圖

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

(重定向自C控制图)

缺點數管製圖(Number of Defects Control Chart，C管製圖)

目錄

1 缺點數管製圖概述
2 缺點數管製圖的理論計算
3 缺點數管製圖的使用條件
4 缺點數管製圖的使用中可能的情形
5 缺點數管製圖實例
6 相關條目

缺點數管製圖概述

　　缺點數管製圖是一種計數值管製圖，能在每一批量的生產中偵測出每一零件或受驗單位不良點的數目。

缺點數管製圖的理論計算

所謂不合格品是指一件物品無法符合一項或多項之規格要求。任何不符合規格之處，稱為一個不合格點(nonconformity)或缺點 (defect)。根據不合格點之嚴重性，我們可能將具有許多不合格點之物品視為合格品。換句話說，具有不合格點之物品，不一定為不合格品。 C管製圖是為了管制一個檢驗單位之總不合格點數。在每一樣本中出現不合格點之機率，服從卜瓦松分配的假設下。每個樣本出現的缺點數是參數為 $λ$ 的 Poisson分配，。

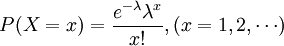
$P(X=x)=\frac{e^{-\lambda}\lambda^x}{x!},(x=1,2,\cdots)$

X即缺點數的隨機變數，因為X設為Poisson分配，故其平均值與變異數都為 $λ$ 。如果管製圖上下限以 $3σ$ 為準，且已知，則管製圖的計算如下：

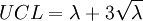
　　 $UCL=\lambda+3\sqrt{\lambda}$

中心線 $= λ$

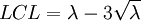
　　 $LCL=\lambda-3\sqrt{\lambda}$

　　其中：UCL 表示控製圖的上控制界限; LCL 表示控製圖的下控制界限;

缺點數管製圖的使用條件

　　因為c管製圖在卜瓦松分配的假設下，有幾項條件必須符合(Grant和Leavenworth l988,Montgomery 1991)：

　　1.在產品出現不合格點之機會(位置)要相當大，而每一特定位置發生不合格點之機率很小且固定。

　　2.每一樣本發生不合格點之機會(範圍)要相同。

　　3.不合格點之發生需為獨立，亦即產品上某一部分發生不合格點不影響其他不合格點之出現。

缺點數管製圖的使用中可能的情形

　　如果 $λ$ 未知， $λ$ 的不偏估計值為平均每樣本上的缺點數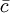 $\bar{c}$ ,

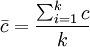
　　 $\bar{c}=\frac{\sum_{i=1}^k c}{k}$

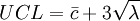
　　 $UCL=\bar{c}+3\sqrt{\lambda}$

　　中心線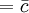 $=\bar{c}$

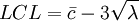
　　 $LCL=\bar{c}-3\sqrt{\lambda}$

缺點數管製圖實例

　　【例】：下表是某汽車工廠生產之車門不合格點數記錄，每組樣本大小為100，試建立管製圖。

樣組	不合格點數	樣組	不合格點數
1	5	14	7
2	8	15	4
3	4	16	9
4	9	17	11
5	12	18	10
6	7	19	6
7	8	20	9
8	12	21	22
9	21	22	13
10	7	23	8
11	12	24	10
12	6	25	7
13	9

　　【解】：

　　此25組樣本共含236個缺點，因此c之估計值為

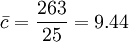
　　 $\bar{c}=\frac{263}{25}=9.44$

　　試用管制界限為

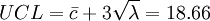
　　 $UCL=\bar{c}+3\sqrt{\lambda}=18.66$

　　中心線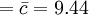 $=\bar{c}=9.44$

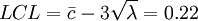
　　 $LCL=\bar{c}-3\sqrt{\lambda}=0.22$

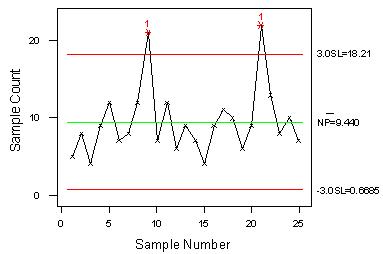
依此25組樣本繪製下麵管製圖:

　　

其中樣本9及21均超出管制界限，因此必須診斷樣本9及21之異常原因。若異常原因已排除後，則可將樣本9及21之數據刪除，並重新計算管制界限，新的不合格點數之平均值為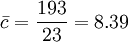 $\bar{c}=\frac{193}{23}=8.39$ 。修正後之管制界限為

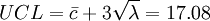
　　 $UCL=\bar{c}+3\sqrt{\lambda}=17.08$

　　中心線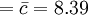 $=\bar{c}=8.39$

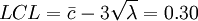
　　 $LCL=\bar{c}-3\sqrt{\lambda}=0.30$

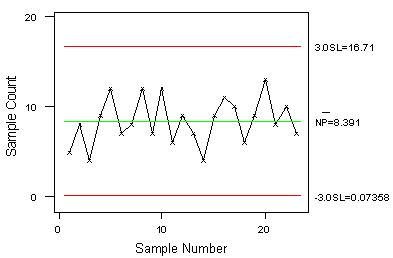
修正後管製圖如下:

　　

相關條目

取自"https://wiki.mbalib.com/zh-tw/%E7%BC%BA%E7%82%B9%E6%95%B0%E7%AE%A1%E5%88%B6%E5%9B%BE"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

Cabbage,Jikaixp,Dan,Yixi,方小莉.

頁面分類: 生產管理工具

評論(共0條)

提示:評論內容為網友針對條目"缺點數管製圖"展開的討論，與本站觀點立場無關。

發表評論請文明上網，理性發言並遵守有關規定。

以上内容根据网友推荐自动排序生成

官方社群

告MBA智库百科用户的一封信

亲爱的MBA智库百科用户：过去的17年，百科频道一直以免费公益的形式为大家提供知识服务，这是我们团队的荣幸和骄傲。然而，在目前越来越严峻的经营挑战下，单纯依靠不断增加广告位来维持网站运营支出，必然会越来越影响您的使用体验，这也与我们的初衷背道而驰。因此，经过审慎地考虑，我们决定推出VIP会员收费制度，以便为您提供更好的服务和更优质的内容。 MBA智库百科VIP会员（9.9元 / 年，点击开通），您的权益将包括： 1、无广告阅读； 2、免验证复制。当然，更重要的是长期以来您对百科频道的支持。诚邀您加入MBA智库百科VIP会员，共渡难关，共同见证彼此的成长和进步！

MBA智库百科项目组

2023年8月10日

闽公网安备 35020302032707号

添加收藏

新建收藏夹

编辑收藏夹

20

公开（该收藏夹未来有关注者后，将无法设为私密）

私密（仅自己可见）