價格優化模型

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

本條目包含過多不是中文的內容，歡迎協助翻譯。

若已有相當內容譯為中文，可逕自去除本模板。

價格優化模型（Price Optimization Models）

價格優化模型簡介

　　價格優化模型（PriceOptimizationModels）比較抽象,我們用收益管理來解讀.原則是將合適的產品在合適的時間，以合適的價格銷售給合適的顧客，並由此使企業在其產品中獲得最大限度的收益。它以市場細分和需求預測為基礎，一方面採取超售（通過超生產規模來接受訂貨）的方法來減少虛假訂貨帶來的不必要的虛耗；另一方面採取存貨控制的方法，將市場細分、需求預測和產品定價緊密結合，最大限度地適應市場需求的多樣性，發掘產品在市場的獲利潛力，實現收益的最大化。　　　　

[編輯]

Price Optimization Models^[1]

25種最流行的管理工具

客戶關係管理

全面質量管理

顧客細分

外包

核心能力

供應鏈管理

戰略規劃

業務流程再造

知識管理

使命書和企業願景書

平衡記分卡

作業基礎管理

忠誠度管理

六西格瑪

戰略聯盟

基準管理

變革管理計劃

增長戰略

經濟附加值增值分析

價格優化模型

開放市場創新

規模定製

情景設定和突發計劃

海外經營

射頻識別

[編輯]

　　Price Optimization Models are mathematical programs that calculate price elasticities, or how demand varies at different price levels, then combine that data with information on costs and inventory levels to recommend prices that will improve profits. Price Optimization Models simulate how customers will respond to price changes, supplementing managers’ instincts with data-driven scenarios. The insights help to forecast demand, develop pricing and promotion strategies, control inventory levels, and improve customer satisfaction.

價格優化模型是計算價格彈性的數學程式，或者需求在不同價格水平上的變化，然後將這些數據與成本和庫存水平的信息結合起來，以推薦能夠提高利潤的價格。價格優化模型模擬了顧客對價格變化的反應，用數據驅動的場景來補充管理者的直覺。洞察力有助於預測需求，制定定價和促銷策略，控制庫存水平，提高客戶滿意度。

[編輯]

Methodology^[1]

　　To implement Price Optimization Models, practitioners should:

Select the preferred optimization model, determine the desired outputs and understand the required inputs;

Collect historical data—including product volumes, the company’s prices and promotions, competitors’ prices, economic conditions, product availability, and seasonal conditions as well as fixed and variable cost details;

Clarify the business’s value proposition and set strategic rules to guide the modeling process;

Load, run and revise the model;

Establish decision processes that incorporate modeling results without alienating key decision makers;

Monitor results and upgrade data input to continuously improve modeling accuracy.

為實施價格優化模型，從業者應:

選擇首選的優化模型,確定所需的輸出和理解所需的輸入;

收集歷史數據包括產品數量,公司的價格和促銷,競爭對手的價格、經濟狀況、產品可用性和季節性條件以及固定和可變成本的細節;

闡明企業的價值定位和戰略規則指導建模過程;

負載,運行和修改模型;

建立決策過程,將建模結果沒有疏遠主要決策者;  監測結果和升級數據輸入,不斷提高建模精度。

[編輯]

Common Uses^[1]

　　Price Optimization Models are used to determine initial pricing, promotional pricing and markdown (or discount) pricing.

Initial price optimization is well-suited to businesses that have a fairly stable base of products with long life cycles, such as grocery, chain drug, and office-supply stores, and manufacturers of commodities like packaging and tools.

Promotional price optimization helps businesses set temporary prices to spur sales of items with long life cycles, such as newly introduced products, products bundled together in special promotions and loss leaders.

Markdown optimization is well-suited to businesses that sell short life-cycle products that are subject to fashion trends and seasonality. Examples include service businesses like airlines and hotels, and certain kinds of specialty retailers, such as apparel retailers, mass merchants and big-box stores.

價格優化模型用於確定初始定價、促銷定價和降價(或折扣)定價。

最初價格優化適合企業,有一個相當穩定的基礎與長生命周期的產品,如食品、連鎖藥品,和辦公商店,和製造商的商品包裝和工具。

促銷價格優化幫助企業臨時定價與長生命周期刺激項目的銷售,如新引進的產品,產品捆綁在一起的特別促銷和損失的領導人。

減價優化適合於銷售短期生命周期產品的企業，這些產品受時尚潮流和季節性因素影響。例如航空公司和酒店等服務行業，以及某些特殊的零售商，如服裝零售商、大眾商家和大賣場。

[編輯]

價格優化模型案例分析^[2]

　　貨物運輸需求通常具有一定的派生性，這種派生性表現為市場對貨物的需求並由此所決定的對貨物的運輸需要，因此，在建立貨物運輸價格模型時必須要考慮三個方面的因素，第一個方面，貨物運輸需求與這些貨物的市場需求密切相關，貨物運輸需求量不可能大於這些貨物的市場需求量；第二個方面，貨物運輸價格與貨物的市場價格緊密相關，貨物的運輸價格需要與貨物市場的價格保持一定的比例關係，為貨物運輸的用戶留有一定的贏利空間，否則，這種派生的運輸需求就有可能消失；第三個方面，貨物運輸企業必須要有一定的贏利，由於存在著多種運輸方式，各種運輸方式之間具有一定的可替代性，所以，這些運輸方式為了追求和擴大各自的利益也存在著競爭。

　　如果將貨物運輸企業的利潤簡單地描述為運輸收入與運輸支出的差額，那麼，可以建立貨物運輸企業的價格優化模型：

　　 $o b . m a x π = R (P (P t l, P q t), Q - C (Q))$ (1)

　　 $s t . P (P t l, P q t) < P d (Q)$ (2)

　　其中： $R (P, Q)$ 表示收入函數， $C (Q)$ 表示支出函數， $P (P t l$ , $p q t$ 表示運輸價格函數， $P d (Q)$ 表示市場價格函數，Q表示運量 $P t l$ 表示鐵路運價， $P q t$ 表示其他運輸方式的運價。目標為在運輸價格低於市場價格的約束下，使收入減支出最大。

　　對於有m種運輸方式和n種運輸貨物的運輸市場，建立價格優化模型：

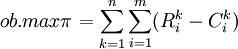　　 $ob.max\pi=\sum^n_{k=1}\sum^m_{i=1}(R^k_i-C^k_i)$ (3)

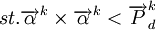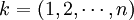
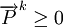
　　 $st.{\overrightarrow\alpha}^k\times{\overrightarrow\alpha}^k<{\overrightarrow P}^k_d$ (4)　　 $k=(1,2,\cdots,n)$ 　　 $\overrightarrow P^k\ge0$

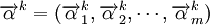　　 ${\overrightarrow\alpha}^k=({\overrightarrow\alpha}^k_1,{\overrightarrow\alpha}^k_2,\cdots,{\overrightarrow\alpha}^k_m)$ (5)

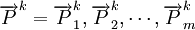　　 ${\overrightarrow P}^k={\overrightarrow P}^k_1,{\overrightarrow P}^k_2,\cdots,{\overrightarrow P}^k_m$ (6)

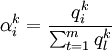　　 $\alpha^k_i=\frac{q^k_i}{\sum^m_{t=1}q^k_l}$ (7)

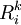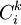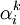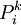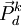　　其中： $R^k_i$ , $C^k_i$ 分別表示第k種貨物通過第i種運輸方式運輸的收入和支出， $\alpha^k_i$ 表示第i種運輸方式運輸的運量占該種貨物各種運輸方式總的運輸量的比例， $P^k_i$ 表示第k種運輸方式運輸第i種貨物的運價水平， $q^k_d$ 表示第k種貨物通過第i種運輸方式運輸的運量， $\vec{P}^k_d$ 表示第k種貨物的市場價格水平。

　　為簡化分析，設 $α k$ 為第k種貨物各種運輸方式的加權平均運價水平占該種貨物的市場價格的比例，則式(4)可以表示為：

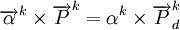
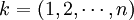　　 ${\overrightarrow\alpha}^k\times{\overrightarrow P}^k=\alpha^k\times{\overrightarrow P}^k_d$ 　　 $k=(1,2,\cdots,n)$ (8)

　　設 $γ k$ 為拉格朗日運算元，構造函數：

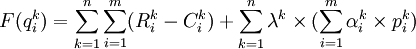　　 $F(q^k_i)=\sum^n_{k=1}\sum^m_{i=1}(R^k_i-C^k_i)+\sum^n_{k=1}\lambda^k\times(\sum^m_{i=1}\alpha^k_i\times p^k_i)$ (9)

　　根據極值條件，有：

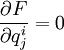　　 $\frac{\partial F}{\partial q^i_j}=0$ 　（共i*j個方程）　　（10）

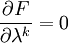　　 $\frac{\partial F}{\partial \lambda^k}=0$ 　（共k個方程）　　（11）

　　其中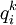 $q^k_i$ 之間存在如下關係：

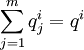　　 $\sum^{m}_{j=1}q^i_{j}=q^i$ 　　（12）

　　並且，式（8）可以表示為：

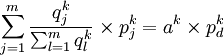　　 $\sum^{m}_{j=1}\frac{q^k_j}{\sum^m_{l=1}q^{k}_{l}}\times p^k_{j}=a^k\times p^k_d$ 　　（13）

　　另外：

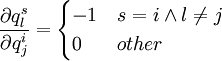　　 $\frac{\partial q^s_l}{\partial q^i_j}=\begin{cases}-1 & s=i \land l\ne j \\ 0 & other\end{cases}$ 　　（14）

　　根據價格彈性(e)定義，如果 $p (q)$ 為價格，q為運量，R為收入，那麼：

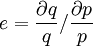　　 $e=\frac{\partial q}{q}/\frac{\partial p}{p}$ 　　（15）

　　並且，

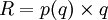　　 $R=p(q)\times q$ 　　（16）

　　依式（15），（16）得式（17）：

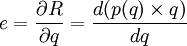
　　 $e=\frac{\partial R}{\partial q}=\frac{d(p(q)\times q)}{dq}$

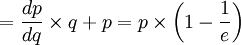　　 $=\frac{dp}{dq}\times q+p=p\times \left(1-\frac{1}{e}\right)$ 　　（17）

　　式中根據彈性的定義，為使e負。

　　將式（17）表示的結果運用到式（10）中，可以得到下式：

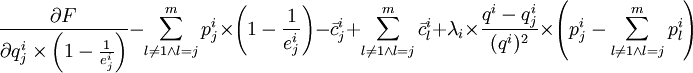　　 $\frac{\partial F}{\partial q^i_{j}\times\left(1-\frac{1}{e^i_j} \right)}-\sum^{m}_{l\ne 1\land l=j} p^i_j\times\left(1-\frac{1}{e^i_j}\right)-\bar{c}^i_j+\sum^{m}_{l\ne 1\land l=j} \bar{c}^i_{l}+\lambda_i\times\frac{q^i-q^i_j}{(q^i)^2}\times\left(p^i_j-\sum^m_{l\ne 1\land l=j} p^i_{l}\right)$ 　　（18）

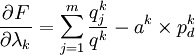　　 $\frac{\partial F}{\partial \lambda_k}=\sum^{m}_{j=1}\frac{q^k_j}{q^k}-a^k\times p^k_{d}$ 　　（19）

　　由此，可以推導出通解（為簡化分析，只考慮兩種運輸方式，即 $j = 1,2$ ）

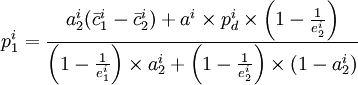　　 $p^i_1=\frac{a^i_2(\bar{c}^i_1-\bar{c}^i_2)+a^i\times p^i_d\times \left(1-\frac{1}{e^i_2}\right)}{\left(1-\frac{1}{e^i_1}\right)\times a^i_2+\left(1-\frac{1}{e^i_{2}}\right)\times(1-a^i_2)}$ 　　（20）

　　其中：

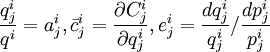　　 $\frac{q^i_j}{q^i}=a^i_j,\bar{c}^i_j=\frac{\partial C^i_j}{\partial q^i_j},e^i_j=\frac{dq^i_j}{q^i_j}/\frac{dp^i_j}{p^i_j}$ ,

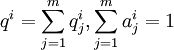
　　 $q^i=\sum^{m}_{j=1}q^i_{j},\sum^{m}_{j=1}a^i_{j}=1$

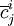　　 $\overline{c}^i_j$ 表示j種運輸方式i品類的邊際成本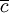， $\overline{c}$ 表示其他各種運輸方式的邊際成本。式（20）可以變形為：

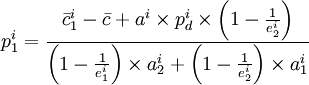　　 $p^i_1= \frac{\bar{c}^i_1-\bar{c}+a^i\times p^i_{d}\times\left(1-\frac{1}{e^i_2}\right)}{\left(1-\frac{1}{e^i_1}\right)\times a^i_2+\left(1-\frac{1}{e^i_2}\right)\times a^i_1}$ 　（21）

　　由模型可以看出，對於某種品類的貨物，運輸價格主要與自身的邊際成本、各種運輸方式的綜合邊際成本、運價水平占貨物市場價格的比例、貨物的市場價格、各種運輸方式的市場份額、貨物的運輸價格彈性以及其他運輸方式的運輸價格等因素有關。其中，邊際成本與運輸距離有關，價格彈性與價格有關，市場占有率與市場總需求量有關。

[編輯]

參考文獻

↑ ^1.0 ^1.1 ^1.2 Darrell Rigby.Management Tools-Price Optimization Models
↑ 徐剛.鐵路貨物運輸市場價格優化模型研究.中國鐵道科學.2003年2月第24捲第1期

取自"https://wiki.mbalib.com/zh-tw/%E4%BB%B7%E6%A0%BC%E4%BC%98%E5%8C%96%E6%A8%A1%E5%9E%8B"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

Cabbage,Smileandblue,Yixi,HEHE林,Solitude1314,Zhangrenren.

頁面分類: 待翻譯的條目 | 管理工具

評論(共1條)

提示:評論內容為網友針對條目"價格優化模型"展開的討論，與本站觀點立場無關。

123.116.68.* 在 2010年9月29日 23:43 發表

很好的議題，可是專業性太強，或者說數學功底這麼深，讓人怎能優化價格呢？有誰知道如何推算“經濟訂單量EOQ”？

回複評論

發表評論請文明上網，理性發言並遵守有關規定。

查看

工具▼

價格優化模型

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

價格優化模型簡介

Price Optimization Models^[1]

Methodology^[1]

Common Uses^[1]

價格優化模型案例分析^[2]

參考文獻

温馨提示

本条目相关课程

本条目由以下用户参与贡献

評論(共1條)

導航

意见反馈

查看

工具▼

價格優化模型

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

價格優化模型簡介

Price Optimization Models[1]

Methodology[1]

Common Uses[1]

價格優化模型案例分析[2]

參考文獻

温馨提示

本條目相關文檔

本条目相关课程

本条目由以下用户参与贡献

評論(共1條)

導航

意见反馈

Price Optimization Models^[1]

Methodology^[1]

Common Uses^[1]

價格優化模型案例分析^[2]