支出函數

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

支出函數(Expenditure Function)

支出函數的概述^[1]

　　支出函數是表示消費者支出的函數。

　　假定效用函數為U=u(x)x是消費的向量，即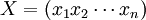 $X=(x_1x_2\cdots x_n)$ ，且有： $x > O N$ 。P為消費的價格向量， $P = (p 1 P 2 c d o t s P n) > O N$ ， $O N$ 是零向量。

　　在這種情況下，支出函數就可定義為：

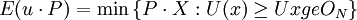
　　 $E(u\cdot P)=\min\left\{P\cdot X:U(x)\ge U xgeO_N\right\}$

　　 $P\cdot x=\sum_{i=1}^n p:x_i$

　　意思是指消費者試圖至少達到用指數u表示的效用或福利水平而使消費成本最小。

　　因此支出函數的推導是在效用既定的條件下，從支出最小化的一階條件中求出補償需求函數

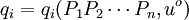
　　 $q_i=q_i(P_1P_2\cdots P_n,u^o)$

　　則支出函數

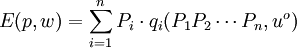　　 $E(p,w)=\sum_{i=1}^n P_i\cdot q_i(P_1P_2\cdots P_n,u^o)$ 。

[編輯]

支出函數與效用函數的關係^[1]

　　支出函數與效用函數存在對偶性關係。如給定特定的正則擬凹效用函數，則產生相應的價格上是一次齊次，在效用上是單調遞增的支出函數，反過來，給定價格上是一次齊次的和效用上是單調遞增的支出函數就產生正則擬凹的效用函數。支出函數除了價格上一次齊次，效用上單調遞增的特性以外，通常還假定

　　(1)為非負函數，即E(P·u)>O；

　　(2)對於P是非遞減的，即 $E (p 1 u) > E (p 2 u), u > O p l > p 2 > O N$ 。

　　(3)E(pu)是凹函數。也就是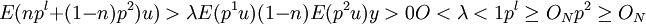， $E(np^l+(1-n)p^2)u)>\lambda E(p^1u)(1-n)E(p^2u)y>0 O<\lambda<1 p^l\ge O_N p^2\ge O_N$ 。

　　支出函數是研究消費者行為的重要的理論方法，支出函數與生產理論中的成本函數極為相似。

[編輯]

參考文獻

↑ ^1.0 ^1.1 梁小民.經濟學大辭典[M].ISBN:7-80061-954-0.團結出版社,1994

取自"https://wiki.mbalib.com/zh-tw/%E6%94%AF%E5%87%BA%E5%87%BD%E6%95%B0"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

Yixi,鲈鱼,苏青荇.

頁面分類: 統計術語

評論(共0條)

提示:評論內容為網友針對條目"支出函數"展開的討論，與本站觀點立場無關。

發表評論請文明上網，理性發言並遵守有關規定。

查看

工具▼

支出函數

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

支出函數的概述^[1]

支出函數與效用函數的關係^[1]

參考文獻

温馨提示

本条目相关课程

本条目由以下用户参与贡献

評論(共0條)

導航

意见反馈

查看

工具▼

支出函數

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

支出函數的概述[1]

支出函數與效用函數的關係[1]

參考文獻

温馨提示

本條目相關文檔

本条目相关课程

本条目由以下用户参与贡献

評論(共0條)

導航

意见反馈

支出函數的概述^[1]

支出函數與效用函數的關係^[1]