大系統理論
出自 MBA智库百科(https://wiki.mbalib.com/)
大系統理論 (large scale system theory)
目錄 |
什麼是大系統理論[1]
大系統理論是指大系統分析、設計、自動控制和實整體最優的理論。大系統理論是現代控制理論的一個重要研領域,主要研究內容包括大系統的建模、模型降階、遞階制、分散控制、穩定性、自動尋優等。其研究對象是工程術、社會經濟、生物生態、軍事系統等領域中規模龐大、結複雜(環節較多、層次較多或關係複雜)、目標多樣、功能合、因素眾多,且含有隨機性的大系統。
大系統理論的形成和發展[1]
早期的控制論和運籌學主要處理中小型非複雜系理論和應用的發展,複雜的大系統、巨系統成為系統主要關心的對象,大系統理論就被提出來了。
由於科技和生產實踐活動的規模只益龐大,科技度日益增加,所涉及的範圍亦越來越廣。在20世紀人們在研究實際系統時不斷發現新問題、帶進新思想觀點、創造了新方法,在現代控制理論、運籌規劃理技術的基礎上形成了跨學科的大系統理論。如1959年我國的秦元勛教授在研究飛機自動駕駛儀設計時,從工程技術處理方法提出了大系統穩定性分解的概念,劉永清教授把這種概念應用在三門峽水電站閘門提升的電力拖動非線性控制系統中,用標量和李亞曾諾夫函數分解法,成功地分析了這個大系統的穩定性。有趣的是,現代控制理論的應用導致了一個兩級的分散控制結構,從實際數據到實際控制的映射通常是在兩級上完成的,其中一個稱為戰略(經濟)級,另一個稱為戰術(穩定)級。戰略級的功能是產生理想的系統響應,常使用一個欲優化的目標函數,進行離線計算;戰術級可用多變數戰術反饋控制器設計。
科技界經過二十多年的努力探討和實踐,目前大系統理論雖不能說成熟完善,但可說已發展到本質水平,其實際應用也取得了可喜的進展,這方面的論文和專著很多。如法國國家科學研究中心的鐵特裡教授領導、著名學者塔穆勒教授和辛格博士等參加的遞階最優化研究小組,把大系統遞階最優化理論用於建造煉鋅工廠和硫磺工廠的遞階控制、太陽能電站的遞階控制、石化複雜過程精煉工段的遞階控制、長途電訊網路管理、英國劍河河水污染控制、熱軋鋼廠粗軋過程鋼帶出口溫度和厚度的控制等問題,都取得了明顯的效益。再如羅馬尼亞的學者應用大系統理論建立了經濟數學模型:巨集觀經濟方面有靜態和動態投入—產出表、技術進步的定量模型、部一級投資最優化模型;微觀經濟方面研究企業之間和企業內部的工段、車間和工種之間的最佳分配、生產配合、庫存最優等,這些研究對羅馬尼亞的國民經濟的發展起到了很好的指導作用。
鐵特裡為代表的學派側重於實際系統模型的研究;以M.D.Mesarovic為代表的美國Case西部儲備大學系統研究中心的學派是以集論為基礎建立複雜決策,制定系統的數學原理和目標;波蘭科學院以R.K.Kulikows Ki為代表的學派是利用管理學、運籌學和數學規劃等領域的概念,應用泛函分析理論為工具來研究多級分解的方法。國外還有一些有成就的學派不再列舉了。
總之,大系統理論目前仍在發展,其應用於實際系統也取得了明顯的效果。我國以秦元勛教授為首在大系統穩定性方面,雖然在20世紀60年代初期做了一些開創性的工作,但在“文革”中中斷了該課題的研究,直至20世紀70年代末期才又開始活躍起來,從理論到應用正在奮起直追,出了不少論文和專著。在應用上如浙大的呂勇哉在首鋼搞的鋼鐵遞階控制很成功,提高產量30%。
將大系統理論用於解決軍事系統方面的問題,其中發展比較迅速,比較突出的是軍用航空航天、火力控制與指揮、指自動化系統等領域。隨著軍事技術的發展,原來的大系統也漸成為中小系統,變成了新的大系統的一個分系統。從而,大系統理論在軍事領域的應用產生了更高的要求和更新的戰。如,對於區域化、大區域化作戰問題中的指揮、控制、信等方面的研究,都是近年來的軍事大系統領域出現的新題,亟待應用大系統理論對其進行合理的分析和解決。
大系統理論的基本內容[2]
大系統理論的基本內容可以概括為兩個方面:
(1)大系統分析。所謂“分析”,是對已有的大系統或設計方案進行定性的和定量的、靜態的和動態的理論分析或試驗研究。其中包括:對系統的環境條件、外部影響因素的分析,對系統現有的運行狀態和性能的估算,對系統的未來發展趨勢和動態進行預測等,以便對系統的技術性能、經濟指標、社會效果、生態影響等各方面作出正確評價,為改善現有系統的運行效能、改進系統組織與管理、選取系統設計方案,提供系統分析的科學依據。
(2)大系統綜合。所謂“綜合”,是對尚待籌建或改建的大系統進行規劃決策與方案設計,制訂協調計劃與組織管理制度,進行系統結構綜合與參數綜合,解決大系統的最優設計、最優控制、最優管理問題,以求所籌建的或擴建的大系統運行經濟合理、技術先進、穩定可靠、協調有序,收到優化的經濟效益和社會效益。大系統的“分析”與“綜合”是相輔相成的:系統分析為系統綜合提供依據,系統綜合又為系統分析提出問題。
大系統理論中有代表性的是“分解協調”方法。也就是把複雜大問題化為簡單小問題。
為了研究不同領域(工程技術、社會經濟、生物生態)的各種大系統,需要抽象出它們的共性。因此,大系統理論主要研究各種大系統的控制與信息過程的共同規律與方法。例如,大系統的結構方案問題。大系統的基本結構方案有:集中控制、分散控制、遞階控制。遞階控制是集中控制與分散控制相結合的產物,是各種大系統普遍採用的結構方案。在工程技術領域,遞階控制是工業生產過程綜合自動化系統的多級電腦控制與管理的典型方案。在社會經濟領域,如國家行政管理系統、軍隊組織體系、經營管理系統等,都採取遞階控制結構方案。在生物生態領域,如人與脊椎動物的中樞神經系統,也具有多級遞階控制結構。同時,值得註意的是,隨著科學技術發展,生產過程自動化系統由集中控制發展為遞階控制;隨著生物進化,生物控制系統也由單神經節發展為多級神經系統。這種發展進化過程的相似性,不同領域中各種大系統結構的相似性,也正是大系統共性的體現。
目前的大系統理論主要是控制理論與運籌學相結合的產物,是以數學模型為基礎的。作為綜合自動化系統的理論和動態系統工程的方法,是系統科學發展的前沿。由於大系統的複雜性及數學模型方法的局限性,大系統理論需要進一步發展與創新。
大系統理論的研究方法[1]
大系統與一般系統有著不同的特性,包括:大型性、複雜性、動態性、不確定性、人為因素性、等級層次性、信息結構能通性等。這些特性軍事大系統也都具備,尤其是後五個特性,更是軍事大系統的固有特性,因此大系統理論的研究方法也同樣適用於軍事大系統。基於前面所列的特性,大系統理論的研究方法與一般系統的研究方法是存在著區別的。下麵就將幾個大系統理論研究方法介紹如下。
(一)大系統建模與分析方法
1.系統動力學建模方法
系統動力學是美國教授福萊斯特首創的一種系統理論,綜合了系統科學和數量經濟學等學科,提出一套系統動力學建模方法。要建立大系統模型,首先要明確系統目標、系統邊界、劃分子系統、明確子系統的相互關係。系統動力學把系統中存在的物流、能流、信息流流體化,提出流位(即狀態)、流率(流位變化率)等概念,把系統目標值與實測值之差類比於流體的壓力差,作為驅動系統傳送信息、進行決策的動力。用反饋環、多重反饋環等概念刻畫系統內部複雜的因果關係,每個反饋環中都包含流率、流位、物流、信息流、耦合等。依據這些資料,建立系統流程圖,簡稱F-圖。依據流程圖,可以寫出描述系統動態特性的微分方程,其主幹部分是流速方程。
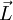 .K:流位向量
.K:流位向量
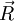 .KL:流率向量
.KL:流率向量
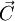 .K:常向量
.K:常向量
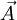 .K:輔助向量
.K:輔助向量
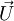 .K:外生向量
.K:外生向量
則流率方程為
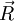 .KL=
.KL=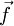 (
(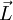 .K,
.K,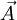 .K,U.K,
.K,U.K,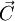 ) (1)
) (1)
對於任意流位,所有流人流率和流出流率的代數和等於流位的導數,因而有
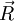 .KL=
.KL=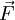 (
(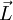 .K,
.K,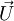 .K,
.K,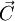 ) (2)
) (2)
有了這一組微分方程後,再編製程式,輸入不同變數作模擬運算,從中選擇合理的方案。流程圖、微分方程組、模擬程式是構成系統動力學模型的主要部分。
2.模糊系統理論建模法
為尋求複雜系統模糊性的數學工具,著名美國系統科學家札德推廣了經典集合概念,建立起模糊集合論,為拓廣數學系統論提供了新的工具。用模糊集合描述系統性態的模糊性,重新闡述系統、信息、控制、系統的表示(如激勵—響應函數)、優化等概念,制定處理有關係統分析、預測、決策、設計、運營中的模糊性的原理和方法,構成所謂模糊系統理論。用模糊集合取代經典集合,給輸入、輸出、狀態、狀態方程、輸出響應函數等概念以模糊的表述,使數學系統論模糊化,就是模糊系統建模的理論依據。在模糊系統理論中,一個具有模糊性的系統S1一般可定義為一個五元組:
S1={U,Y,X,δ1,σ1} (3)
其中,U為輸入空間,Y為輸出空問,X為狀態空間,δ1與σ1分別是模糊狀態轉移函數和模糊輸出函數。這就是模糊系統的狀態空間表達式。根據具體的系統特性,還可以寫出具有特定形式的模糊系統的數學模型。
3.灰色系統理論建模法
灰色系統理論是我國學者鄧聚龍創立的。依據人對系統信息掌握的程度,可將系統分為三類:信息完全明確的白色系統,信息部分明確的灰色系統和信息完全不明確的黑色系統。描述灰色系統的主要概念有灰色數、灰色方程、灰色矩陣、灰色群等等。參數不能確知其具體值,只能限定其可能取值的區間時,稱為灰數,一般記作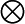 。已知下限為0的一個連續型參數,可以表示為
。已知下限為0的一個連續型參數,可以表示為
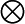 ∈(0,∞) (4)
∈(0,∞) (4)
這是連續灰數。某人年齡在30至35之間,可能取6個值,這是離散灰數,可表示為
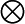 ∈{30,31,32,33,34,35} (5)
∈{30,31,32,33,34,35} (5)
包含灰數的方程為灰方程,如
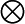 x+1=0 (6)
x+1=0 (6)
是一個灰色代數方程,戈項的參數為灰數。由於可取多個值,上式代表的是一個方程組。包含灰色導數的方程,叫做灰微分方程。
灰色系統理論的建模法由以下五個步驟組成:
(1)明確問題、對象的因素、關係、目標、條件並用簡練語言表示出來,稱為語言模型;
(2)將語言模型中各因素按前因與後果關係配對,用方框與箭頭表示,作為一個環節,描述各環節關聯方式的方框圖,稱為網路模型;
(3)將表示各環節數量關係的數據填人方框圖,稱為量化模型;
(4)建立動態模型;
(5)對動態過程品質不令人滿意的模型做參數、環節、結構方面的調整,稱為優化模型。
系統動力學建模法,模糊系統理論建模法,灰色系統理論建模法等方法,共同的特點是定性分析與定量分析相結合、經驗和理論相結合、分析計算與模擬實驗相結合,模型構造、參數確定具有一定的主觀性。這些都反映了大系統的特點。
(二)大系統控制方法
大系統的合理控制方式是集中控制與分散控制相統一,稱為遞階控制。實際存在的大系統都是某種遞階控制的系統,大系統共有的等級層次結構特征,是與這種控制方式相適應的。如前面所述,主要存在三種類型的控制方式:多級遞階控制、多層遞階控制和多段遞階控制。
1.多級遞階控制
按受控對象或過程的結構特征將大系統劃分為各小系統,按決策權力劃分為各等級,同一級的各控制中心相互獨立的工作,下一級接受上一級的指令信息,控制過程中信息主要在上下級之間傳送。圖1表示了一個三級遞階控制系統。這種控制方框圖呈塔形,或為嵌套式結構。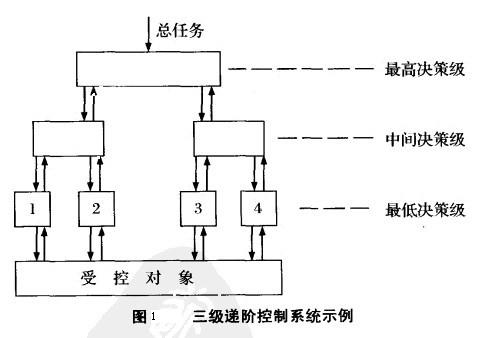
2.多層遞階控制
按任務或功能將系統分為各層次,較高層次的任務或功能更綜合,須對付不經常的或緩慢變化的擾動;較低層次的任務或功能較單純,須對付經常性或快變的擾動。如一個生產車間,廠一級控制月生產目標,相應於較長期的市場變化;車間一級控制日生產率,須對付短期擾動。圖2是一個二層遞階控制系統的示例圖。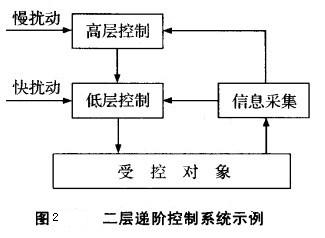
各層次之間既有“分工”負責,又隱含有領導與被領導關係。低層控製作用取決於高層下達的信息或對象的信息,高層依據對象的反饋信息進行控制。
3.多段遞階控制
按受控時序分為若幹段,每段作為一個較小系統來控制,再按各段之間的銜接關係進行協調控制。圖3是一個三段遞階控制系統。分段控制級與協調級之間有縱向信息聯繫,又通過協調級形成橫向信息聯繫。通常導彈飛行過程就是分解為主動段、慣性飛行段、末端制導段來控制的。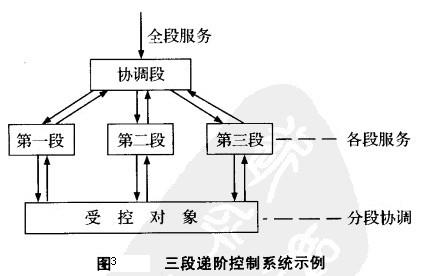
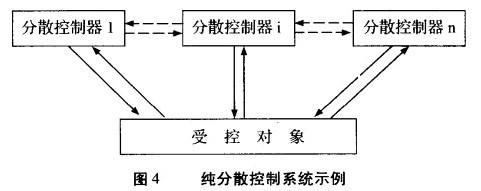
完全分散控制的大系統不是不需要協調,而是不通過專設的協調級來協調,因而如何協調是一個很重要的問題。信息分散化、控制分散化是大系統中的一個重要類型,針對這種情況,必須提出新的概念和方法,建立適應這種類型大系統特點的控制理論。
(三)大系統的可靠性
系統在規定的條件下和規定的時間內無功能故障運行的能力,稱為系統的可靠性。更廣義地講,系統發生故障後的複原能力,也屬於可靠性。可靠性是衡量系統性能優劣的重要指標,大系統尤其如此。
衡量可靠性的定量指標主要有平均無故障工作時間、可靠度、失效度、失效率、故障平均修複時間、維修度等,都是在統計意義下定義的特征量。設取N個同種組件或系統進行可靠性試驗,Ti為第i個組件出現第一次故障以前的正常工作時間,則平均無故障工作時間T為
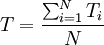 (7)
(7)
系統在規定時間間隔[0,t]內能夠正常工作的概率,稱為系統的可靠度,記作R(t)。系統工作時刻後,單位時間內發生失效或故障的概率,稱為失效率,記為λ(t)。可靠度與失效率有如下關係:
 (8)
(8)
若λ為常數,或者λ代表平均失效率,則有
R(t)=e-λt (9)
T與λ的關係為
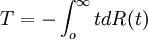 (10)
(10)
平均失效率λ與F的關係為
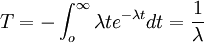 (11)
(11)
T、R、λ是衡量系統可靠性的最主要參數。
設系統S由n個子系統S1,S2…,Sn組成,Si的可靠性為Ri(t),且各子系統的故障獨立無關,系統沒有備份。那麼,根據概率關係,系統S的可靠性為R
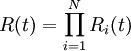 (12)
(12)
令F(t)記系統的不可靠度,則有
R(t)+F(t)=1 (13)
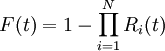 (14)
(14)
上面兩式表明,無備份條件下,系統包含的子系統越多,它的可靠性就越差。對於可靠性問題在大系統中的特殊尖銳性,這是一個量的證明。
系統是由元素(元件)和子系統(組件)組成的,元件和子系統的可靠性固然影響整個系統的可靠性,系統的可靠性還與系統的組織結構有關。如果系統的構成部分有備份或重覆“線路”,並且按照精巧的方式組織起來,使系統整體不受單個部分的故障的影響,那麼系統可靠性就是非常高的。假定一個系統中的某個組件重覆或備份n次,該種組件的可靠性均為R(t),則個組件全部出現故障的概率為
P = (1 − R(t))n (15)
由於0<R(t)<1,當n很大時,系統發生故障的概率將非常小。這表明,用大量不太可靠的部件按照重覆“線路”或設置備份方式組織起來的系統,可以有很高的可靠性。1952年,馮·諾伊曼首先發現了這個原理,經過多年的發展,現已建立起具有豐富內容的容錯理論,包括自我診斷理論、檢錯糾錯理論、最優備份切換理論和功能恢復理論等,並相應地發展了各種容錯技術,為大系統的可靠性問題提供了最基本的解決辦法和較高的保障。
大系統理論的應用[3]
實際上,現代管理所面臨的對象大多屬於大系統。它們不僅規模大、因素多、相互聯繫複雜,而且目標多樣,功能綜合,尤其是“管理人”、自動化機器以及加速變化的環境因素等,交叉作用,綜合效應,使管理系統的最優控制更加複雜和困難。這就要求正確運用大系統論和方法來研究、處理現代管理問題,以實現最優化的或滿意的整體控制目標。
1.管理大系統分析
它是指對已有的大系統及其設計方案,進行定性和定量的理論分析和實際研究。包括對管理大系統的環境條件以及內部各子系統之間的物質、能量和信息聯繫的分析;對大系統現有運行狀況的估計和對其未來發展趨勢的預測;等等。以便對其技術性能、經濟指標、社會效果,生態影響等作出評價,尋找改進現有性能和運行效率的途徑,為選擇最優決策和控制方案等,提供理論方法和實驗依據。
2.管理大系統綜合
這是指對將要籌建或改建的管理大系統,進行規劃決策,總體設計,對籌建過程和實際運動實施計劃協調、組織管理,從而解決管理大系統的最優設計、控制和管理等問題。這裡需要指出的是,整合原則在管理大系統綜合中具有重要作用,是實現管理大系統綜合的有效手段和途徑。
3.管理大系統的分解和協調
在絕大多數管理大系統研究和設計中,傳統的演繹法和歸納法往往是不夠用的。它首先就不能回答管理大系統最優的目標是什麼。即使有可能知道其整體最優目標,也難以找到如何建構能夠確保實現最優目標的管理大系統。但是,如果我們按如下思路來考查:當管理大系統整體沒有可能成為最優化對象的時候,首先考慮將多變數的複雜系統按一定方式和原則進行“系統分割”,將管理大系統(S)分割為幾個子系統(S1,S2,S3……Sn)。然後分別解決各子系統的分析和綜合,並求局部最優化。最後根據管理大系統的總目標或總任務,對各子系統進行強有力的協調和控制,努力尋求各子系統之間的最優協調配合,以達到管理大系統整體目標的近似最優。這就是管理大系統的“分解——協調”理論和方法的基本內容。如,某計劃部門編製年度生產計劃。一般是先由其所屬各部門編出各自的局部最優計劃(分解),然後由計劃部門彙總並予以適當調整,在修改各部門計劃的基礎上,達到該計劃部門的整體計劃最優和近似最優(綜合)。這些步驟一般要求運用“窮舉法”或單純形法,反覆比較,組合與計算,直到充分滿意為止。需要指出的是,當某個管理大系統的某一特點比較突出且與總目標直接相關,而其他特點可以忽略不計,就可運用一般控制和最優化的有關理論和方法實現最優控制,達到最優目標。
管理大系統的分解可分為目標分解和模型分解兩種。目標分解是把管理大系統的總任務或總目標分解為各子系統的子任務或子目標。例如,企業可將總的生產任務和技術經濟指標分配到各車間。通常,管理大系統的目標是可分解的,且其總目標函數可視為各子系統目標函數的代數和。但是,各子系統的相互影響也不容忽視,這種影響就形成了管理大系統數學模型中的相互關聯,它對總目標的實現影響極大。因此,關鍵在於模型分解。即把高階、高維的管理大系統數學模型分解為低階、低維的子系統數學模型,網路模型或物理模型,以便於計算、求解並優化。管理大系統的模型分解,實質上就是通過數學的。網路的或物理的方式建模。這就既能突出管理大系統的主要性能,又能剋服複雜大系統的“維數災”,使問題得到簡化。就管理系統的數學模型分解而言,目前已有多種方法能夠實現其模型簡化。如,集結法就適用於線性管理大系統,它能將變數很多的管理大系統模型集結(集中、簡化)為變數較少的集結模型,並保證其主要動態性能不變;攝動法則能夠將原管理大系統高階方程中所含的小參數(即對該管理大系統只起次要的、微擾作用的,在某些情況下可不予考慮的參變數)的攝動項(或稱微干擾項)設法予以略去,即關聯平衡原則和關聯預估原則。其實質是根據各子系統偏差的反饋信息,整合協調變數,從而實現對各子系統的協調控制。在各子系統局部最優化基礎上,選擇最優的協調變數,以滿足“關聯平衡條件”和“關聯預估條件”,從而實現管理大系統整體目標最優化。








學習了,謝謝