古諾模型

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

古諾模型（Cournot model）

什麼是古諾模型

　　古諾模型又稱古諾雙寡頭模型（Cournot duopoly model），或雙寡頭模型（Duopoly model）,古諾模型是早期的寡頭模型。它是由法國經濟學家古諾於1838年提出的。是納什均衡應用的最早版本，古諾模型通常被作為寡頭理論分析的出發點。古諾模型是一個只有兩個寡頭廠商的簡單模型，該模型也被稱為“雙頭模型”。古諾模型的結論可以很容易地推廣到三個或三個以上的寡頭廠商的情況中去。

　　古諾模型假定一種產品市場只有兩個賣者，並且相互間沒有任何勾結行為，但相互間都知道對方將怎樣行動，從而各自怎樣確定最優的產量來實現利潤最大化，因此，古諾模型又稱為雙頭壟斷理論。

　　^[1]

經濟分析工具

埃奇沃斯盒狀圖

埃奇沃斯模型

伯特蘭德模型

巴斯塔布爾標準

純生產率效應

彩票選擇實驗

ELES模型

方差比率檢驗

古諾模型

國際卡特爾

霍特林模型

貨幣先行模型

價格領導模型

價格卡特爾

均衡分析法

經濟系統工程

經濟控制論模型

卡特爾模型

肯普標準

穆勒標準

偏好誘導實驗

70規則

斯威齊模型

斯塔克爾伯格模型

薩繆爾森經濟學方法論

社會核算矩陣

討價還價模型

消費者剩餘

希爾施模型

演化經濟學方法論

滯後變數模型

自動估值模型

[編輯]

古諾模型的假定^[2]

　　兩個生產者的產品完全相同；生產成本為零(如礦泉水的取得)；需求曲線為線性，且雙方對需求狀況瞭如指掌；每一方都根據對方的行動來做出自己的決策，並都通過凋整產量來實現最大利潤。

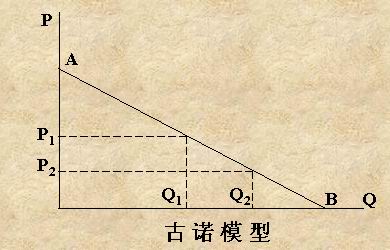
　　如圖，AB為產品的需求曲線，總產量為OB，開始時假定A廠商是唯一的生產者，為使利潤最大，其產量 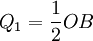$Q_1=\frac{1}{2}OB$ (按MC=0 假設，OB中點的產量使得MR=MC=0)，價格為 $P 1$ 。當B廠商進入該行業時，認為A將繼續生產 $Q 1$ 的產量，市場剩餘銷售量為 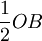$\frac{1}{2}OB$ ，為求利潤最大，B廠商的產量 $Q 1 Q 2$ 將等於 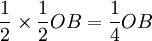$\frac{1}{2}\times\frac{1}{2}OB=\frac{1}{4}OB$ ，價格下降到 $P 2$ 。B廠商進人該行業後，A廠商發現市場剩餘銷售量只剩下 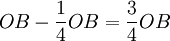$OB-\frac{1}{4}OB=\frac{3}{4}OB$ ，為求利潤最大化，它將把產量調整到 $\frac{1}{2}\times\frac{3}{4}OB=\frac{3}{8}OB$ 。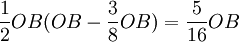A廠商調整產量後，B廠商將再把產量調整到 $\frac{1}{2}OB(OB-\frac{3}{8}OB)=\frac{5}{16}OB$ 。這樣，兩個寡頭將不斷地調整各自的產量，為使利潤為最大，每次調整，都將產量定為對方產量確定後剩下的市場容量的 $\frac{1}{2}$ 。

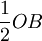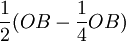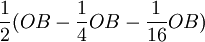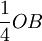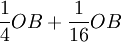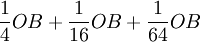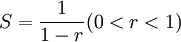　　這樣，A廠商產量調整序列為 $\frac{1}{2}OB$ 、 $\frac{1}{2}(OB-\frac{1}{4}OB)$ 、 $\frac{1}{2}(OB-\frac{1}{4}OB-\frac{1}{16}OB)$ ……，B廠商產量調整序列為 $\frac{1}{4}OB$ 、 $\frac{1}{4}OB+\frac{1}{16}OB$ 、 $\frac{1}{4}OB+\frac{1}{16}OB+\frac{1}{64}OB$ ……。則A廠商的均衡產量為 $OB[\frac{1}{2}-(\frac{1}{2^3}+\frac{1}{2^5}+\ldots)]$ ，B廠商的均衡產量為 $OB[\frac{1}{2^2}+\frac{1}{2^4}+\frac{1}{2^6}+\ldots]$ 。根據無窮幾何級數和的公式 $S=\frac{1}{1-r}(0<r<1)$ ，我們得到：

　　A的均衡產銷量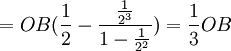 $=OB(\frac{1}{2}-\frac{\frac{1}{2^3}}{1-\frac{1}{2^2}})=\frac{1}{3}OB$

　　B的均衡產銷量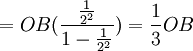 $=OB(\frac{\frac{1}{2^2}}{1-\frac{1}{2^2}})=\frac{1}{3}OB$

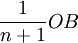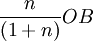　　如果寡頭壟斷市場內有n個廠商，我們可求出每個廠商的均衡產量為 $\frac{1}{n+1}OB$ ，總產量為 $\frac{n}{(1+n)}OB$ 。要是完全競爭的市場結構，廠商數目越多，單個廠商的產銷量越小，而總產量 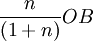$\frac{n}{(1+n)}OB$ 就越大；如果是完全壟斷的市場結構，廠商的產銷量則為 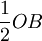$\frac{1}{2}OB$ 。故寡頭市場的總產量大於壟斷市場的產量，小於完全競爭市場的總產量。

[編輯]

古諾模型中廠商的產量選擇

　　A廠商的均衡產量為：

　　OQ（1/2―1/8―1/32―……）=1/3 OQ

　　B廠商的均衡產量為：OQ（1/4+1/16+1/64+……）=1/3 OQ

　　行業的均衡總產量為：1/3 OQ+1/3 OQ=2/3 OQ

[編輯]

價格競爭的古諾模型^[2]

　　以上討論的古諾模型是產量競爭模型。對於那些生產同質產品的寡頭來說，所進行的競爭屬於產量競爭，如石油生產者之間的競爭就是如此。如果寡頭們所生產的是有差別的同類產品，例如，汽車生產者之間的競爭則大多是價格競爭。我們用一個簡單隨意的例子討論價格競爭的古諾模型。

　　假定有兩個寡頭分別用40元(也可以設想為40萬元)的固定成本生產可以相互替代並巳是有差別的產品。為了使問題簡化，假定不存在變動成本，因此邊際成本等於0。加上變動成本後並不會改變問題的結論。兩個寡頭所面臨的市場需求函數如下:

　　D1： $Q 1 = 24 - 4 P 1 + 2 P 2$ 　　　　①

　　D2： $Q 2 = 24 - 4 P 2 + 2 P 1$ 　　　　②

　　其中， $Q 1$ ，與 $Q 2$ 分別表示寡頭1與寡頭2的產出水平； $P 1$ 與 $P 2$ 分別表示寡頭1與寡頭2收取的價格。可以看出，對每個寡頭產品的需求量與該寡頭產品的價格反方向變化，與競爭對手產品的價格同方向變化。假定兩個寡頭同時作出決策。在進行決策時，每個寡頭都把其對手的價格視為既定，然後選擇能使自己利潤達到最大化的自己產品的價格，通過構造兩個寡頭的利潤函數，並按照求利潤最大化的條件，可以導出古諾均衡解。例如，對於寡頭1來說，其利潤函數為

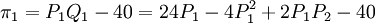　　 $\pi_1=P_1Q_1-40=24P_1-4P_1^2+2P_1P_2-40$ 　　　　③

　　按照求利潤最大化的條件就(③)式對寡頭1產品的價格 $P 1$ 求一階導數並令一階導數值等於0。得到寡頭1的反應函數:

　　 $P_1=3+\frac{P_2}{4}$ 　　　　④

　　同理，可以導出寡頭2的反應函數:

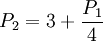　　 $P_2=3+\frac{P_1}{4}$ 　　　　⑤

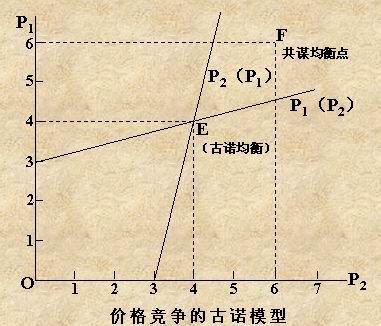
　　求(④)式與(⑤)式的聯立解，得到可以使兩個寡頭利潤最大化的均衡價格 $P 1 = 4$ ， $P 2 = 4$ 。寡頭間無勾結行為而達到的這種均衡稱為古諾均衡。圖中E點是價格競爭的古諾均衡點。

　　圖中的兩條曲線(本例中為直線) $P 1 (P 2)$ 與 $P 2 (P 1)$ 分別為寡頭1與寡頭2的反應曲線。兩條區線的交點為古諾均衡點。在我們的例子中，雖然兩個寡頭所進行的是價格競爭，但是競爭的結果卻是兩個寡頭收取相同價格，無任何價格差別，似乎不算價格競爭。需要指出，兩寡頭收取同樣的價格是偶然的。價格競爭的結果可能是寡頭收取同樣的價格，也可能是收取不同的價格。

　　將所求出的均衡價格 $P 1 = 4$ 、 $P 2 = 4$ 分別代入兩寡頭的需求函數(①、②)式，得到兩寡頭的均衡產量，分別為 $Q 1 = 16$ ， $Q 2 = 16$ 。將均衡價格與均衡產量代入(③)式的利潤函數，得到兩個寡頭的最大化利潤， $π 1 = 24$ , $π 2 = 24$ 。

　　古諾均衡是在寡頭間無勾結行為時達到的均衡。若寡頭間相互勾結，以求得聯合的利潤最大化，所達到的均衡是共謀均衡。就(①、②)兩式的需求函數而言，如果兩個寡頭進行勾結。其聯合的利潤函數為

　　 $π = π 1 + π 2 = 48 P - 4 P 2 - 80$ 　　　　④

　　利潤最大化的價格為P=6，兩寡頭利潤最大化的產量分別為 $Q 1 = 12$ ， $Q 2 = 12$ 。每個寡頭所獲得的最大化利潤為 $π 1 = 32$ , $π 2 = 32$ ：。圖中F點是共謀均衡點。顯然，寡頭在進行勾結的情況下收取的價格與獲得的利潤都高與無勾結行為下的價格與利潤，但產出水平低於無勾結行為下的產出水平。

[編輯]

古諾模型結論的推廣

　　以上雙頭古諾模型的結論可以推廣。令寡頭廠商的數量為m，則可以得到一般的結論如下：

　　每個寡頭廠商的均衡產量=市場總容量/（m+1）

　　行業的均衡總產量=市場總容量·m/（m+1）

　　古諾模型的缺陷是假定了廠商以競爭對手不改變產量為條件。

[編輯]

參考文獻

↑ 許純禎,吳宇暉,張成輝.西方經濟學=Economics[M].高等教育出版社,2008.10.
↑ ^2.0 ^2.1 許純禎.西方經濟學.高等教育出版社,1999年07月第1版

取自"https://wiki.mbalib.com/zh-tw/%E5%8F%A4%E8%AF%BA%E6%A8%A1%E5%9E%8B"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

蔓草寒烟,Vulture,JACK,山林,funwmy,Wwdz,Angle Roh,Kane0135,Cabbage,Dan,Doveflies,Yixi,章鱼大丸子,HEHE林,Mis铭,188****1791,150****2199,M id c1523e209ef9c15bec6448da9b5e1125.

頁面分類: 經濟分析工具 | 壟斷理論

評論(共20條)

提示:評論內容為網友針對條目"古諾模型"展開的討論，與本站觀點立場無關。

Cysol (討論 | 貢獻) 在 2010年1月10日 20:06 發表

好像有點問題吧...古諾是產量決策，伯川德才是價格決策吧...faint

回複評論

Angle Roh (討論 | 貢獻) 在 2010年1月11日 15:23 發表

Cysol (討論 | 貢獻) 在 2010年1月10日 20:06 發表

好像有點問題吧...古諾是產量決策，伯川德才是價格決策吧...faint

是的，古諾模型是產量決策的模型。文中提到的應該是價格競爭的古諾模型，在寡頭無勾結的情況下，達到利潤最大化時，兩個寡頭的價格相等，這就是古諾均衡。當然，這種價格相等只是最終的結果，在競爭中則不同。最終結果只是一種趨勢，現實中的價格競爭是一個不會中止的過程。所以正常情況仍是價格不相等。如果兩個寡頭勾結，價格也相等，但高於無勾結時，產量就減少了。

回複評論

152.78.219.* 在 2010年12月25日 19:51 發表

圖不對。兩邊都應該是Q.一邊是Seller1 另一邊是seller2

回複評論

Dan (討論 | 貢獻) 在 2011年2月12日 11:19 發表

152.78.219.* 在 2010年12月25日 19:51 發表

圖不對。兩邊都應該是Q.一邊是Seller1 另一邊是seller2

添加了部分內容及參考文獻，希望對你有幫助！

回複評論

211.101.37.* 在 2011年5月24日 15:36 發表

圖真的真的不對啊親！改了吧……

回複評論

220.191.168.* 在 2011年10月8日 10:46 發表

看不懂。。。。。。。。。

回複評論

99.59.0.* 在 2011年11月14日 04:19 發表

第一塊的0Q是指市場原來的equilibrium quantity麽？

回複評論

138.38.158.* 在 2011年11月16日 06:04 發表

152.78.219.* 在 2010年12月25日 19:51 發表

圖不對。兩邊都應該是Q.一邊是Seller1 另一邊是seller2

圖確實錯了

回複評論

Yixi (討論 | 貢獻) 在 2011年11月16日 10:41 發表

138.38.158.* 在 2011年11月16日 06:04 發表

圖確實錯了

附上參考文獻，希望對您有幫助哦~

回複評論

76.93.33.* 在 2012年2月22日 16:50 發表

你上述的圖 p1,p2是bertrand model的.. 以價格為競爭手段. 請更正.

回複評論

219.140.196.* 在 2012年7月9日 15:30 發表

古諾模型的圖是對的..沒有問題.. AB是市場中的線性需求函數不是廠商的代號..OB是總產量..當A廠商壟斷要獲得最大利潤時..需要P*Q最大..給定線性函數AB下.PQ乘積在中點最大..故A壟斷時產量為Q1..此時市場上剩餘產量為Q1B..B廠商為獲最大利潤取中點Q2(同上理)..後面的推導就如文中所說的了..

回複評論

183.56.143.* 在 2012年11月22日 22:07 發表

請問古諾模型的前提假定是成本不變還是邊際成本不變啊！

回複評論

92.143.236.* 在 2012年12月9日 20:29 發表

MC=0中的MC是什麼意思啊

回複評論

Dan (討論 | 貢獻) 在 2012年12月10日 10:31 發表

92.143.236.* 在 2012年12月9日 20:29 發表

MC=0中的MC是什麼意思啊

邊際成本MC；邊際收益MR

回複評論

165.91.149.* 在 2015年9月15日 11:27 發表

D1：Q1 = 24 − 4P1 + 2P2　　　　① ????????????

回複評論

68.5.22.* 在 2015年12月14日 13:19 發表

92.143.236.* 在 2012年12月9日 20:29 發表

MC=0中的MC是什麼意思啊

MC is Marginal Cost

回複評論

LarinTermin (討論 | 貢獻) 在 2016年10月30日 14:35 發表

最大化 // 最人化

回複評論

LarinTermin (討論 | 貢獻) 在 2016年10月30日 14:37 發表

時 // 寸

回複評論

Mis铭 (討論 | 貢獻) 在 2016年10月31日 09:56 發表

LarinTermin (討論 | 貢獻) 在 2016年10月30日 14:37 發表

時 // 寸

謝謝指正，已修改！

回複評論

梁传靖 (討論 | 貢獻) 在 2018年12月16日 15:18 發表

調整；字錯了 // 通過凋整產量

回複評論

發表評論請文明上網，理性發言並遵守有關規定。

查看

工具▼

古諾模型

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是古諾模型

古諾模型的假定^[2]

古諾模型中廠商的產量選擇

價格競爭的古諾模型^[2]

古諾模型結論的推廣

相關條目

參考文獻

温馨提示

本条目相关课程

本条目由以下用户参与贡献

評論(共20條)

導航

意见反馈

查看

工具▼

古諾模型

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是古諾模型

古諾模型的假定[2]

古諾模型中廠商的產量選擇

價格競爭的古諾模型[2]

古諾模型結論的推廣

相關條目

參考文獻

温馨提示

本條目相關文檔

本条目相关课程

本条目由以下用户参与贡献

評論(共20條)

導航

意见反馈

古諾模型的假定^[2]

價格競爭的古諾模型^[2]