利率平價理論
出自 MBA智库百科(https://wiki.mbalib.com/)
利率平價理論 (Interest Rate Parity Theory)
目錄 |
利率平價理論 (Interest Rate Parity Theory)認為兩個國家利率的差額相等於遠期兌換率及現貨兌換率之間的差額。由凱恩斯和愛因齊格提出的遠期匯率決定理論。他們認為均衡匯率是通過國際拋補套利所引起的外匯交易形成的。在兩國利率存在差異的情況下,資金將從低利率國流向高利率國以謀取利潤。但套利者在比較金融資產的收益率時,不僅考慮兩種資產利率所提供的收益率,還要考慮兩種資產由於匯率變動所產生的收益變動,即外匯風險。套利者往往將套利與掉期業務相結合,以避免匯率風險,保證無虧損之慮。大量掉期外匯交易的結果是,低利率國貨幣的現匯匯率下浮,期匯匯率上浮;高利率國貨幣的現匯匯率上浮,期匯匯率下浮。遠期差價為期匯匯率與現匯匯率的差額,由此低利率國貨幣就會出現遠期升水,高利率國貨幣則會出現遠期貼水。隨著拋補套利的不斷進行,遠期差價就會不斷加大,直到兩種資產所提供的收益率完全相等,這時拋補套利活動就會停止,遠期差價正好等於兩國利差,即利率平價成立。[1]因此我們可以歸納一下利率平價說的基本觀點:遠期差價是由兩國利率差異決定的,並且高利率國貨幣在期匯市場上必定貼水,低利率國貨幣在期匯市場上必定升水。
利率平價理論核心觀點[2]
通過利率同即期匯率與遠期匯率之間的關係來說明匯率的決定與變動的原因。該學說認為遠期差價是由兩國利差決定的,(遠期匯率的升水、貼水率約等於兩國間的利率差異)並且高利率貨幣在遠期市場上必定貼水,低利率貨幣在遠期市場上必為升水,在沒有交易成本(transaction cost)的情況下,遠期差價等於兩國利差,即利率平價(interest parity)成立。
利率平價理論的基本內容[3]
利率平價理論可分為無拋補利率平價(Uncovered Interest Rate Parity, UIRP)和拋補的利率平價(Covered Interest Rate Parity, CIRP)兩種。此兩者的不同之處在於對投資者的風險偏好所做的假定上。
對於投資者按風險分類:風險厭惡者需要獲得一定的風險報酬才願意持有風險資產;與此相反,風險愛好者願意獲得承擔風險的權利,但其會付出一定代價;而風險中立者則願意在沒有風險收益的情況下承擔風險。
(一)無拋補利率平價
定義:在資本具有充分國際流動性的條件下,投資者的套利行為使得國際金融市場上以不同貨幣計價的相似資產的收益率趨於一致,也就是說,套利資本的跨國流動保證了“一價定律”適用於國際金融市場。
決定機制:
利率的變化取決於無風險條件下投資者的投機決策,即
(1)在年終若持有單位本幣的存款與收益額大於持有外幣存款與收益額按預期匯率 折算成的本幣款,即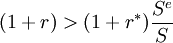 ,則在本國存款;
,則在本國存款;
(2)在年終若持有單位本幣的存款與收益額小於持有外幣存款與收益額按預期匯率 折算成的本幣款,即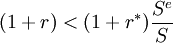 ,則在外國存款;
,則在外國存款;
(3)在年終若持有單位本幣的存款與收益額等於持有外幣存款與收益額按預期匯率 折算成的本幣款,即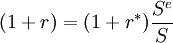 ,則在任何一國存款均可。
,則在任何一國存款均可。
其中, r表示以本幣計價的資產收益率(年率),r * 表示外幣計價的相似資產的平均收益率,S表示即期匯率(直接標價),Se表示預期將來某個時點(比如年末)的預期匯率。並且這裡假設投資者是風險中性(Risk Neutral)。
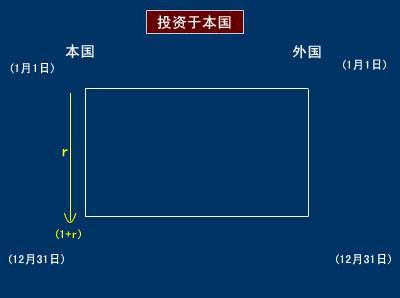
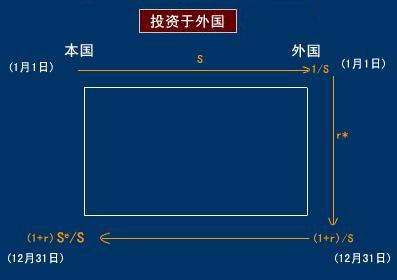
本國居民持有一單位本國貨幣,既可以將其存放於國內銀行按國內利率取得收益,也可以將其按即期匯率S兌換成外國貨幣投放國外銀行,按外國利率取得收益,用圖—1、圖—2來表示:
圖—1
圖—2
最終兩者的收益趨於相等:
在風險中性的前提下,投資者只需比較一下兩種資產的收益:如果收益不等,投資者就會涌向一種資產,資本涌入國會因投資的增加而收益率遞減,而流出國的收益率則可能會抬高, 最終兩者的收益趨於相等:
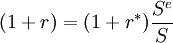 (1)
(1)
如果預期匯率的變動率為ΔSe,則:
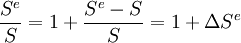 (2)
(2)
那麼式(1)可表述為:
(1 + r) = (1 + r * )(1 + ΔSe) = 1 + r * + ΔSe + r * ΔSe。
其中,r * ΔS是兩個比率的積,是一個“二階小量”,忽略不計,於是上式變為:
ΔSe = r − r * (3)
無拋補利率平價的含義:本國利率高於(低於)外國利率的差額等於本國貨幣的預期貶值(升值)幅度。
(二) 拋補的利率平價
定義:拋補利率平價,與無拋補利率平價相比,拋補的利率平價並未對投資者的風險偏好做出假定,即套利者在套利的時候,可以在期匯市場上簽訂與套利方向相反的遠期外匯合同(掉期交易),確定在到期日交割時所使用的匯率水平。
通過簽訂遠期外匯合同,按照合同中預先規定的期遠期匯率進行交易,以達到套期保值的目的。由於套利者利用遠期外匯市場固定了未來交易時的匯率,避免了匯率風險的影響,整個套利過程可以順利實現。套利者如果在即期達成一筆一年期外匯交易,
用數學表達是:
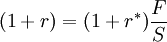 (4)
(4)
其中,F (Forward rate)表示在即期(比如1月1日)公佈的在1年後(比如12月31日)交割的遠期匯率。它實際上是替代了公式(1)中的 Se (Expected Future Spot rate)。若令 f (Forward premium) 表示遠期的升水(或貼水),即一國的遠期匯率超過(低於)即期匯率的比率,則有
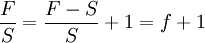 (5)
(5)
那麼,拋補的利率平價可更為清楚地表達為
f = r − r * (6)
在推算中,r * f同樣被作為二階小量被省去。
拋補利率平價含義:
(1)本國利率高於(低於)外國利率的差額等於本國貨幣的遠期貼水(升水)。
(2)高利率國的貨幣在遠期外匯市場上必定貼水,低利率國的貨幣在該市場上必定升水。如果國內利率高於國際利率水平,資金將流入國內牟取利潤。
(3)拋補利率平價中,套利者不僅要考慮利率的收益,還要考慮由於匯率變動所產生的收益變動。
結論:在資本具有充分國際流動性的前提下,拋補與無拋補的利率平價均告訴我們:如果本國利率上升,超過利率平價所要求的水平,本幣將會預期貶值;反之,則升值。
利率平價理論的思想起源可以追溯到l9世紀60年代。l9世紀90年代,研究遠期外匯理論的德國經濟學家沃爾塞·洛茨提出了利差與遠期匯率的關係問題。
20世紀初期,凱恩斯第一個建立了古典利率平價模型,得出以下結論:
1、決定遠期匯率的基本因素是貨幣短期存款利率之間的差額。
2、遠期匯率圍繞利率平價上下波動。
3、不論遠期匯率與其利率平價偏離多大程度,獲得足夠利潤的機會使套利者把資金轉移到更有利的金融中心。
4、如果外匯交易被少數集團控制,或在主要交易人之間達成交易協議,那麼,掛牌匯率可能偏離其利率平價。
5、套利資金有限,常常不能大到足以使遠期匯率調整到其利率平價水平上。
6、在不兌換紙幣的條件下,銀行利率變化直接促使遠期匯率重新調整。
20世紀30一40年代,保羅·艾因齊格運用動態均衡思想,發展了利率平價的動態理論。經過羅伯特·z·阿利布爾等人的進一步完善,現代利率平價理論框架趨於成熟。
現代利率平價理論的代表人物主要有特森·格魯貝爾、沃費克爾和威利特等人。與傳統的利率平價理論不同的是,利率平價的現代理論認為,套利者對遠期外匯的超額需求不具有完全彈性(傳統理論認為是呈完全彈性)。這就是說,遠期匯率不僅受套利者行為的影響,而且也受到貿易商、投資者和中央銀行等諸多外匯市場的參與者的影響。因此,遠期匯率就不僅由套利決定,而且與套利者對即期匯率的預期有關。
對利率平價理論的評價[3]
自20世紀20年代利率平價被首次提出後,利率平價受到西方經濟學家的重視。它與購買力平價所不同的是考察資本流動(而不是商品流動)與匯率決定之間的關係,它從一個側面闡述了匯率變動的原因——資本在國際間的流動,利率平價同樣並非是一個完善的匯率決定理論,對其的批評主要有:
1.利率平價的實現依據是國際金融市場上的“一價定律”, 但現實中,不僅完善的外匯市場沒有普遍存在,而且許多國家實際對外匯實行管制並對資本流動進行限制。
“一價定律”的先決條件是:
(1)有效的且處於完全自由競爭狀態的外匯市場。即需要一個有組織的即期和遠期外匯市場,市場的信息能夠非常有效地流通,從而消除可能出現的機會利潤;
(2)無市場壁壘,資本在國際間的流動不受任何限制;
(3)交易成本很低或可以基本忽略不計。
2.在利率平價的關係式當中,並未能表明到底是利率平價決定匯率,還是即期匯率與遠期匯率的差距來決定利率。
3.忽視利率結構問題。
利率平價說沒有考慮交易成本。然而,交易成本卻是很重要的因素。如果各種交易過高,就會影響套利收益,從而影響匯率與利率的關係。如果考慮交易成本,國際間的拋補套利活動在達到利率平價之前就會停止。
利率平價說假定不存在資本流動障礙,假定資金能順利,不受限制地在國際間流動。但實際上,資金在國際間流動會受到外匯管制和外匯市場不發達等因素的阻礙。目前,只有在少數國際金融中心才存在完善的期匯市場,資金流動所受限制也少。
利率平價說還假定套利資金規模是無限的,故套利者能不斷進行拋補套利,直到利率平價成立。
但事實上,從事拋補套利的資金並不是無限的。這是因為:
與持有國內資產相比較,持有國外資產具有額外的風險。隨著套利資金的遞增,其風險也是遞增的。
套利還存在機會成本,由於套利的資金數額越大,則為預防和安全之需而持有的現金就越少。而且這一機會成本也是隨套利資金的增加而遞增的。基於以上因素,在現實世界中,利率平價往往難以成立。
- ↑ 夏大慰,劉勤主編;劉鳳委,張英奎,劉勤等編著.公司戰略與風險管理.中國財政經濟出版社,2009.04.
- ↑ 朱孟楠.廈門大學.國際金融學. 第二章 外匯與匯率 第四節 匯率理論及其評價
- ↑ 3.0 3.1 《國際經濟學》.第十章 匯率的決定.第三節 利率平價理論.西北師範大學 經濟管理學院
本条目由以下用户参与贡献
Angle Roh,苦行者,山林,funwmy,Zfj3000,18°@鷺島,Dan,Cabbage,ROURTW,泡芙小姐,HEHE林,Tiffany,罗茜,Lin,张介平,Tracy,M id 33102b7c5aa30123ac49f7d914825224,M id 0fda389224938afbbdc3e0bd9945ebee.評論(共18條)
r − r * = ΔEe 應該 是r − r * = ΔEe(1+r)吧,別誤人了
感謝提出錯誤之處,現已對內容進行了整理,不足之處,歡迎指正
r − r * = ΔEe 應該 是r − r * = ΔEe(1+r)吧,別誤人了
由於ΔEe(1+r)=ΔEe+ΔEe*r,而ΔEe*r相對於其他幾個值是很小的,為簡便,可以將其省略。類似的省略並不少見
感謝Derek8687的提醒,已將缺失部分進行補充。
MBA智庫百科是可以自由參與編輯的百科,發現錯誤和不足您也可以參與修改和編輯哦!
r − r * = ΔEe 應該 是r − r * = ΔEe(1+r)吧,別誤人了
你指出錯誤的地方是好事,但你用“誤人”兩個字就不對了。人家辛苦寫出來的東西,你要尊重別人的勞動。
你指出錯誤的地方是好事,但你用“誤人”兩個字就不對了。人家辛苦寫出來的東西,你要尊重別人的勞動。
你說的那一項因為太小被忽略了。








Ee △= —— - 1 吧? E