無拋補利率平價
出自 MBA智库百科(https://wiki.mbalib.com/)
無拋補利率平價(Uncovered Interest Rate Parity,UIRP)
目錄 |
無拋補利率平價是指在資本具有充分國際流動性的條件下,投資者的套利行為使得國際金融市場上以不同貨幣計價的相似資產的收益率趨於一致,也就是說,套利資本的跨國流動保證了“一價定律”適用於國際金融市場。
利率的變化取決於無風險條件下投資者的投機決策,即
(1)在年終若持有單位本幣的存款與收益額大於持有外幣存款與收益額按預期匯率 折算成的本幣款,即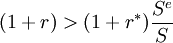 ,則在本國存款;
,則在本國存款;
(2)在年終若持有單位本幣的存款與收益額小於持有外幣存款與收益額按預期匯率 折算成的本幣款,即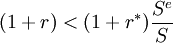 ,則在外國存款;
,則在外國存款;
(3)在年終若持有單位本幣的存款與收益額等於持有外幣存款與收益額按預期匯率 折算成的本幣款,即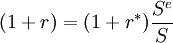 ,則在任何一國存款均可。
,則在任何一國存款均可。
其中, r表示以本幣計價的資產收益率(年率),r * 表示外幣計價的相似資產的平均收益率,S表示即期匯率(直接標價),Se表示預期將來某個時點(比如年末)的預期匯率。並且這裡假設投資者是風險中性(Risk Neutral)。
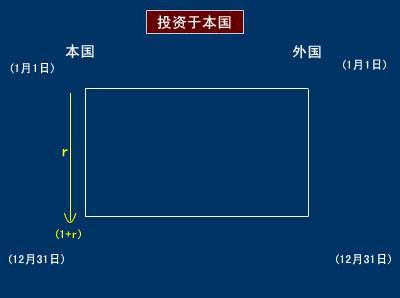
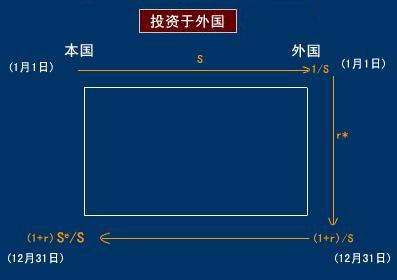
本國居民持有一單位本國貨幣,既可以將其存放於國內銀行按國內利率取得收益,也可以將其按即期匯率S兌換成外國貨幣投放國外銀行,按外國利率取得收益,用圖—1、圖—2來表示:
圖—1
圖—2
最終兩者的收益趨於相等:
在風險中性的前提下,投資者只需比較一下兩種資產的收益:如果收益不等,投資者就會涌向一種資產,資本涌入國會因投資的增加而收益率遞減,而流出國的收益率則可能會抬高, 最終兩者的收益趨於相等:
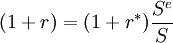 (1)
(1)
如果預期匯率的變動率為ΔSe,則:
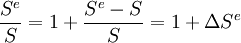 (2)
(2)
那麼式(1)可表述為:
(1 + r) = (1 + r * )(1 + ΔSe) = 1 + r * + ΔSe + r * ΔSe。
其中,r * ΔS是兩個比率的積,是一個“二階小量”,忽略不計,於是上式變為:
ΔSe = r − r * (3)
無拋補利率平價的含義:本國利率高於(低於)外國利率的差額等於本國貨幣的預期貶值(升值)幅度。








解釋得很清楚,很到位。