斯塔克尔伯格模型

出自 MBA智库百科(https://wiki.mbalib.com/)

斯塔克尔伯格模型或称斯塔克尔伯格竞争 (Stackelberg Leadership Model, Stackelberg Competition)由德国经济学家斯塔克尔伯格（H. Von Stackelberg）在上世纪30年代提出。

　　在古诺模型和伯特兰德模型里，竞争厂商在市场上的地位是平等的，因而它们的行为是相似的。而且，它们的决策是同时的。当企业甲在作决策时，它并不知道企业乙的决策。但事实上，在有些市场，竞争厂商之间的地位并不是对称的，市场地位的不对称引起了决策次序的不对称，通常，小企业先观察到大企业的行为，再决定自己的对策。德国经济学家斯塔克尔伯格建立的模型就反映了这种不对称的竞争。

　　该模型的假定是：主导企业知道跟随企业一定会对它的产量作出反应，因而当它在确定产量时，把跟随企业的反应也考虑进去了。因此这个模型也被称为“主导企业模型”。

　　假设厂商1先决定它的产量，然后厂商2知道厂商1的产量后再作出它的产量决策。

　　因此，在确定自己产量时，厂商1必须考虑厂商2将如何作出反应。

　　其他假设与古诺模型相同，

　　斯塔克尔伯格模型是一个产量领导模型，厂商之间存在着行动次序的区别。产量的决定依据以下次序：领导性厂商决定一个产量，然后跟随者厂商可以观察到这个产量，然后根据领导性厂商的产量来决定他自己的产量。需要注意的是，领导性厂商在决定自己的产量的时候，充分了解跟随厂商会如何行动——这意味着领导性厂商可以知道跟随厂商的反应函数。因此，领导性厂商自然会预期到自己决定的产量对跟随厂商的影响。正是在考虑到这种影响的情况下，领导性厂商所决定的产量将是一个以跟随厂商的反应函数为约束的利润最大化产量。在斯塔克尔伯格模型中，领导性厂商的决策不再需要自己的反应函数。

　　一、斯塔克尔伯格港口竞争机制模型

　　这里所说的港口竞争指的是同一港口群内不同港口之间的竞争。一个区域内往往形成一个港口群，群内港口面临共同的陆向或者海向腹地，因而竞争激烈。港口服务的提供需要具备临海的地理位置，且港口投资的成本大，这些条件的存在限制了港口产业中港口的数量，使得进入港口的产业进入壁垒较大，因而也就决定了港口产业的市场结构。

　　假设在开始阶段，某区域只有一个港口1，其内陆腹地流出或流向该腹地的所有产品均通过港口1，那么港口1完全垄断市场。假设不存在进入成本，即新港口以任意规模的投资进入均可获得收益，于是潜在进入者港口2可以以任意规模进入市场，并获得利润。下面基于斯塔克尔伯格模型，从产量方面说明港口之间的竞争。

　　斯塔克尔伯格模型用来描述一个充当领导者角色的厂商与作为追随者的厂商之间的相互影响。假设在所有的港口中存在一个在该行业中处于支配地位的港口，该处于支配地位的港口是斯塔克尔伯格领导者。斯塔克尔伯格领导者对产量的选择将直接导致市场价格的变化，从而影响其他追随者改变自己的产量。同样，处于支配地位的港口产量(对其货物、集装箱的吞吐量的选择)发生变化，供给的变化导致市场价格(港口货物、集装箱装卸、航运价格、泊位费用等费用)变化，而市场价格的变化又促使其他港口改变各自的产量，以保持利润最大化。港口之间博弈的主体是能决定港口产量的政府或者企业。假设条件如下：

　　1．有两个港口1、2，港口1是产量领导者，产量为y₁，港口2是跟随者，即根据港口1的选择而选择产量y₂。市场价格是总产量的函数，即p = f(y₁ + y₂)；反需求函数可以认为是p = a − b(y₁ + y₂)。

　　2．港口1、2均根据自己的产量确定最大化利润，且两个港口的边际成本为0。

　　3．由于港口1在整个行业处于支配地位，港口2将在港口1产量确定的情况下实现利润最大化，而港口1也知道港口2根据自己产量确定它的产量，即完全信息。

　　4．港口2根据港口1确定产量，对港口2而言，港口1的产量是常量，港口1在选择产量时也会考虑到其对港口2的影响。

　　由于其成本假设为0，港口2的利润函数为：

　　，

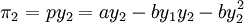　　利润最大化的条件：，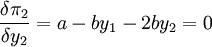

　　所以，求得反应函数：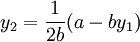

　　将上面的反应函数代入港口1的利润函数：

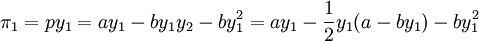
　　其利润最大化条件：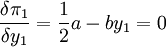

　　所以均衡时港口1最大利润化的产量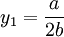

　　那么，同理可以求出港口2最大利润化的产量：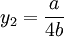

　　在斯塔克尔伯格模型下均衡时两个港口的产量分别为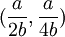：此时港口1、港口2的收益分别为：

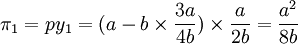
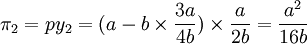
　　这样，在港口1的产量领导下，港口1和港口2实

　　现了短期的均衡，均衡时的产量为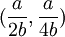，市场价格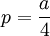。港口1获得的利润大于港口2的利润，说明了先动者的优势，并且，港口1通过产量的选择限制了港口2的进入规模。

　　二、斯塔克尔伯格港口竞争机制模型的扩展

　　我们定义港口产量是港口投入资本量的函数，存在下列函数关系：Y=f(K)，其反函数K = f ^{− 1}(Y)代表港口产量的多少取决于它的资本存量多少。事实上，进入港口行业需要大量的投资，其沉没成本很大，需要较大的进入成本。所以，把进入成本F引入模型，在规模收益递增的情况下，小规模的进入不能获得利润。正是因为进入成本大，才使在位者港口可以遏制其他竞争者的进入。

　　在进入成本存在的情况下，港口2进入市场后的利润函数变为：

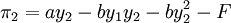
　　那么，在位者港口1通过制定产量Y₁，使得港口2的最大利润满足maxπ₂ = 0，这样港口2因进入市场无利可图而不进入，港口1通过产量的选择阻止港口2进入，阻止进人的产量水平由下式确定：

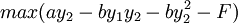
　　港口2取得最大利润的条件：

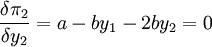
　　所以，当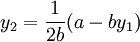 时，港口2的利润最大，最大利润为：

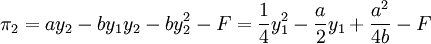
　　港口1选择自己的产量y₁，使港口2的利润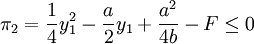

　　若式子 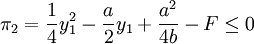，即满足

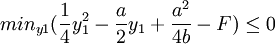
　　y₁=a时，上式有最小值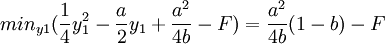

　　所以，当满足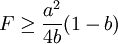时，港口2利润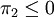

　　下面分别对几种情况进行讨论：

　　1. 当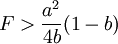 时，

　　y₁的取值范围满足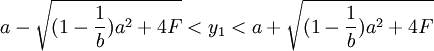时，π₂ < O；

　　y₁取其他值时，π₂ > O。

　　2. 当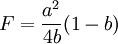 时，y₁ = a时，π₂ = 0；

　　y₁取其他值时，π₂ > 0。

　　3. 当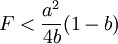 时，π₂ > 0。此时，进入壁垒较小，因而不管港口1怎样调整自己的产量，都不能阻止港口2进入市场。

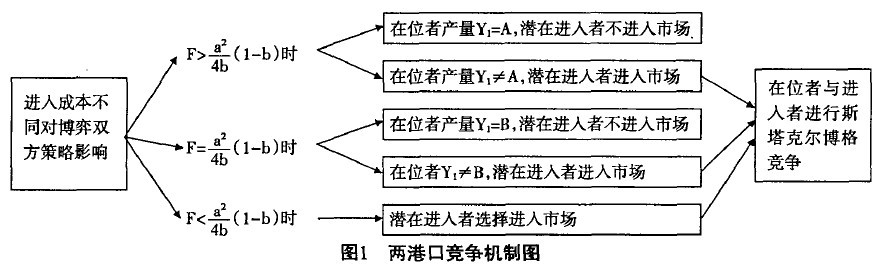
　　由上面的模型可以说明港口之间的竞争机制：在位者根据竞争者进入成本的大小选择遏止其进入还是默许进入策略；而竞争者或者潜在进入者却只能根据其进入成本大小选择进入还是不进入市场。港口1要根据港口2进入成本的大小，选择对港口2的策略。如果港口2的进入成本满足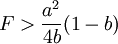，在这种情况下，港口1选择产量的范围如果满足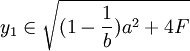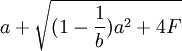，，此时港口1的资本投资存量为K₁ = f ^{− 1}(Y₁)，港口1的资本量构成了进入壁垒，阻止了港口2的进入；如果港口2的进入成本满足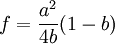，则港口1只需常量调整为y₁ = a，就能使得港口2即使进入市场，其获得的利润为π₂ = 0，但是港口1无论选择除了y₁ = a的任何产量，港口2进入市场均会获得利润，此时港口2进入，市场中将会有两个港口，且港口l是领导者，港口2是跟随者；如果港口2的进入成本满足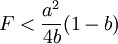，此时的进入成本较小，港口1无论怎样选择产量，港口2的进入都会获得利润，此时，市场上将存在港口1、港口2两个港口，港口1是产量领导者，港口2是跟随者，两个港口之间的竞争机制是斯塔克尔博格式的竞争。记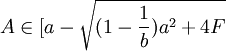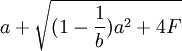，，B=a，两港口之间的竞争机制图如图l所示。

　　三、环渤海港口竞争的实证分析

　　环渤海港口群包括了辽宁、河北、天津和山东的主要港口，包括大小港口60多个，其中包括大连、秦皇岛、天津、青岛四个亿吨大港。环渤海港口群根据地理空问位置可以分为三大子港口群：一是以大连为核心的辽宁港口群，包括锦州港、营口港、丹东港几个主要支线港；二是以天津为核心的津冀港口群，包括秦皇岛港、京唐港、黄骅港等主要支线港；三是以青岛港为核心的山东港口群，包括烟台港、威海港、龙口港、日照港等支线港。 本文所研究的港口竞争，指的是环渤海港口群港口之间内部的竞争，不考虑环渤海港口群中港口与国外港口的竞争，也不考虑环渤海港口群与国内其他港口群之间的竞争。环渤海港口群港口之间的竞争又包括了集群内部枢纽港的竞争和大港与周围小港之间的竞争。

　　(一)环渤海港口群内部枢纽港的竞争

　　枢纽港是港口的核心，对区域经济发展起到十分重要的作用。环渤海港口群内部枢纽港的竞争主要集中在大连、天津、青岛之间，其中大连港要成为东北亚国际航运中心，天津港要成为北方国际航运中心，而青岛港也要成为国际航运中心。

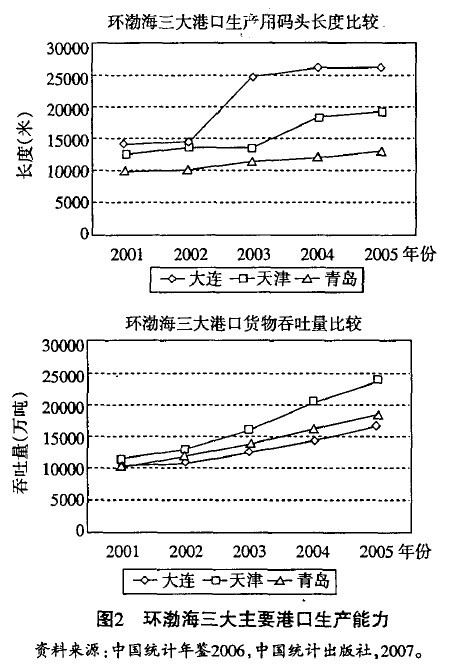
　　港口投资用于增加港口生产用码头的长度，进而增加了港口的货物吞吐能力，或者集装箱吞吐能力。这三个主要港口的竞争在于对港口规模的投资上，港口之间的竞争以增加对货物的吞吐量为主，港口通过增加港口码头长度和码头泊位个数来增加自身的吞吐能力，从图2中我们可以看出，2002至2003年间，大连港生产用码头增长幅度较大，而天津港2003到2004年年间增长幅度较大，青岛港生产用码头长度虽然增幅不大，但近几年来一直稳步增加。虽然大连港生产用码头的长度大于青岛和天津港，但是其货物吞吐量是其中最小的，可见通过扩大港口规模来增大货物吞吐量的效果并不明显，说明港口规模只是影响货物吞吐量的一个因素。

　　(二)区域内小港之间的竞争

　　区域内大港与周围小港之间的竞争主要表现为辽宁港口群内港口之间的竞争，津冀港口群内以及山东港口群内港口之间的竞争，产生竞争的原因由于各个港口地理位置上比较接近，所服务的内陆腹地相同或者交叉，而对于货主而言，选择他们当中哪个港口其综合成本没有区别或者区别不大，因而各港口之间围绕腹地资源展开竞争。港口腹地的界限并不明确。内陆地区产品出口或进口不一定就近选择距离港口，他们在选择港口时考虑的是综合的成本，不单单是考虑运费，还应考虑影响综合成本的其他因素，包括港口的效率、航运班次等等。规模较大的港口之间的竞争依靠产量(吞吐量)，通过港口规模的不断扩大，获得规模经济优势，从而降低自身的平均成本。而小港口由于自然条件的限制，以及巨大的投资成本，不可能象大港口那样进行巨大的投资以获得规模经济，因而规模小的港口主要通过降低服务价格，提高服务质量来争夺腹地资源，在货主通往其他港口的运输成本一致的情况下，通过降低其他方面的成本达到降低货主的综合成本，以此来吸引货源。

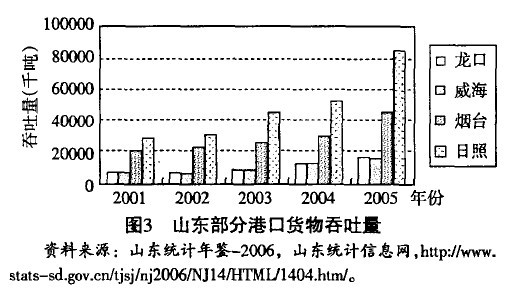
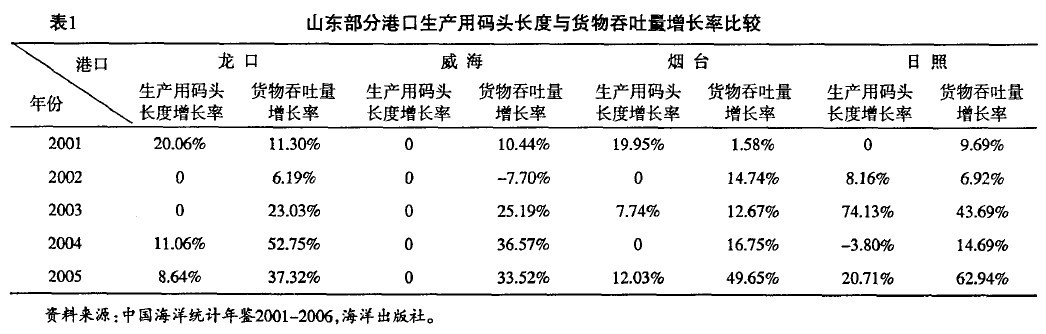
　　由图3可以看出，山东港口群的这些港口年货物吞吐能力整体上逐年上升，在没有考虑青岛的情况下，货物吞吐量最大的是日照，到2005年，日照港的货物吞吐量达到84 208千吨，烟台港2005年的货物吞吐量达到45 060千吨，龙口港和威海港这两个港口的年货物吞吐量类似，几年来也处于缓慢上升阶段。但是，这些港口的货物吞吐量增长比率并不与其生产用码头长度增长率相一致。在不考虑其他因素的条件下，生产用码头长度的增加到第二年才会表现出货物吞吐能力的增长。表1所列的是各年来山东部分港口生产用码头长度增长率与货物吞吐量增长率，从表中我们可以看出，前一年生产用码头长度并不一定与后一年吞吐量有着正相关的关系，或者说，即使生产用码头长度的增加并不一定能使吞吐量在下一年有所增长。这就说明了港口规模的扩大不一定是港口货物吞吐量增加的主要原因，还有其他因素影响这港口的货物吞吐量，小港口之间的竞争，通过投资增加吞吐量，这种竞争方式不是很明显，而是通过其它方式来争夺货源。

　　根据以上的分析，我们可以看出，无论是生产用码头的增加还是货物吞吐量的增加，都是扩大港口规模的结果，这也说明了环渤海港口之间的竞争机制，即围绕产量进行竞争，各个港口均通过规模的扩大获得更多的市场份额，也充分说明原来原先潜在进入者进入市场的进入壁垒并不足以限制其进入，因而在位者也无法通过自身产量的选择来限制其他潜在进入者的进入，对跟随者港口的策略影响也较小，竞争的结果是潜在进入者最终进入市场，作为领导者的港口和作为跟随者的港口均扩大产量，增加对货物的吞吐能力，各个港口通过货物吞吐能力的增加展开竞争。

　　之所以作为产量领导者的大港和作为跟随者的小港展开产量竞争，以及作为潜在进入者的其他竞争者进入市场，充分说明港口产业的市场结构还处于寡头或者垄断竞争中，港口数量还没有足够的多，只要潜在进入者进入该市场的预期收益高于其进入成本，潜在进入者就会进入，直至市场的饱和或者说是达到近似完全竞争状态。当然，建立一个港口需要有适合的自然条件，这也就在一定程度上限制了港口产业中的港口数目，进而决定了各个港口之间的竞争是不完全竞争，从而使得以扩大产量为主的竞争机制得以运行。

　　四、对策措施

　　港口之间的适度竞争，有助于提高港口的服务效率，降低物流成本，可以增强港口的国际竞争力，促进港口的发展。但是，我们在提倡港口竞争的同时，要避免或者减少港口的盲目竞争、恶性竞争。由于整个环渤海港口群由于在地域上的相似性，再加上港口功能的可替代性，导致了群内各个港口相互争夺腹地资源，在这个过程中，各个港口运用各种手段，容易造成港口的盲目竞争，盲目竞争主要指港口间的同质化、低水平化的竞争，表现在数量、价格方面的竞争。港口之间的盲目竞争将造成很大的问题：首先，巨大的资本投入造成了资源的浪费。盲目竞争会造成对港口的大规模投入，港口投资费用高，而且时间长，如果过多的资本投资于港口建设中，形成大量的重复建设，将会造成资本的大量浪费，不利于国民经济的增长；其次，港口的盲目竞争容易造成整个环渤海港口群整体上开发的盲目性，使环渤海港口群内港口格局混乱，不利于形成对外的核心竞争力；第三，港口的盲目竞争，不利于港口的专业化、技术化水平的提高。盲目竞争使得各个港口往往只注重增加吞吐量，而忽视了增加吞吐量的方式，各个港口容易只将重点放在规模的扩大上，忽视港口作业的专业化、技术化水平的提高；最后，盲目竞争使得在对海岸线资源进行开发的过程中只注重开发，而对海岸线资源的保护程度不够。由于海岸线资源是不可再生资源，无秩序的开发不利于可持续发展。

　　鉴于上述问题，我们在保证港口竞争的同时，还要遏制盲目竞争、恶性竞争，因而提出以下建议。

　　1．环渤海港口群要根据自身优势，加强港口之间的分工和协作，通过分工与协作，作好港口资源的整合工作。港口之间的分工与合作主要是大港与大港、小港与小港以及大港与小港之间的分工与合作。大港之间，小港之间要根据自身优势来进行分工，而大港与小港之间，主要是小港作好支线服务，为区域大港、枢纽港吸引更多的货源。港口之间更好的进行分工和协作，有助于实现区域内港口资源的合理配置，避免了港口的重复建设。要实现港口的分工合作，需要发挥港口优势，实现环渤海港口群的一体化。由于环渤海港口群的各个港口分属于不同的省市，因而港口之间能否进行分工和协作关键要看省市之间的协商，以及利益分配。

　　2．提倡港口的“错位竞争”、合理竞争。各个港口应对港口功能进行合理定位，根据自身情况选择港口的主要功能，比如枢纽型港口、腹地型港口或者转口型港口的转变，以及选择作为基本港还是非基本港。港口竞争是不可避免的，关键是要避免恶性竞争，港口之间要进行合理的竞争。合理的竞争就是港口之间服务质量、效率水平上的竞争，以此代替以前的港口间的数量、价格竞争，促进整个港口群的结构优化。

　　3．政府相关部门应制定合理的港口发展规划，同时政府部门要对港口建设发挥监督管理作用。由于港口对于国家和地区的经济发展有着极为重要的作用，因而港口的发展应该有个合理的长远的计划，在考虑到港口所在区域发展的同时，还要兼顾国家利益。由于环渤海港口群内的港口分属于不同的行政区，各个省市在制定各自的港口发展战略时要充分考虑到整个港口群的发展，各省市要加强沟通和联系，在保证国家利益的前提下制定辖区内的港口发展战略。

　　4．扩展港口物流战略联盟。战略联盟指企业之间利用股权或契约方式形成的一种组织形式，而港口联盟是战略联盟的一种具体的表达方式，是港口与港口间为了得到更大的收益通过协商达成一致对外形式。它既可指几个港口组成的集团，也可指与船公司的联盟，与内陆运输组织的联盟等。为了使环渤海港口群内港口资源得到有效利用，需拓展国内外港口战略联盟，尤其在物流方面。通过战略联盟的扩展可以扩大港口服务的范围，有利于增加港口产量而又避免了港口之间在产量上的恶性竞争。

• 伯特兰德模型
• 斯威齐模型
• 古诺模型
• 埃奇沃斯模型